What Expressivity Theory Misses: Message Passing Complexity for GNNs (2509.01254v1)

Published 1 Sep 2025 in cs.LG

Abstract: Expressivity theory, characterizing which graphs a GNN can distinguish, has become the predominant framework for analyzing GNNs, with new models striving for higher expressivity. However, we argue that this focus is misguided: First, higher expressivity is not necessary for most real-world tasks as these tasks rarely require expressivity beyond the basic WL test. Second, expressivity theory's binary characterization and idealized assumptions fail to reflect GNNs' practical capabilities. To overcome these limitations, we propose Message Passing Complexity (MPC): a continuous measure that quantifies the difficulty for a GNN architecture to solve a given task through message passing. MPC captures practical limitations like over-squashing while preserving the theoretical impossibility results from expressivity theory, effectively narrowing the gap between theory and practice. Through extensive validation on fundamental GNN tasks, we show that MPC's theoretical predictions correlate with empirical performance, successfully explaining architectural successes and failures. Thereby, MPC advances beyond expressivity theory to provide a more powerful and nuanced framework for understanding and improving GNN architectures.

Summary

The paper introduces Message Passing Complexity (MPC), a continuous measure that quantifies the practical difficulty of a task for a given GNN architecture.
It employs a probabilistic, lossy variant of the Weisfeiler-Leman test to capture real-world challenges like over-squashing and under-reaching in message propagation.
Empirical results show that MPC aligns with performance trends and provides actionable guidance for GNN architectural design and model selection.

Message Passing Complexity: A Task-Specific Framework for GNN Analysis

Introduction and Motivation

The analysis of Graph Neural Networks (GNNs), particularly Message Passing Neural Networks (MPNNs), has been dominated by expressivity theory, which characterizes the ability of an architecture to distinguish non-isomorphic graphs, typically via the Weisfeiler-Leman (WL) test. However, this binary, isomorphism-based framework is fundamentally limited in its ability to explain or predict empirical performance on real-world tasks. The paper "What Expressivity Theory Misses: Message Passing Complexity for GNNs" (2509.01254) introduces Message Passing Complexity (MPC), a continuous, task-specific measure that quantifies the practical difficulty of solving a given task with a given GNN architecture. MPC is rooted in a probabilistic, lossy variant of the WL test and is designed to bridge the gap between theoretical expressivity and practical performance, capturing phenomena such as over-squashing and under-reaching that are invisible to classical expressivity theory.

Limitations of Classical Expressivity Theory

Classical expressivity theory provides only binary statements: a model can or cannot distinguish certain graphs, with the WL test as the canonical reference. This approach suffers from several critical limitations:

Idealized Assumptions: Theoretical results assume lossless information propagation and unbounded depth, which are not achievable in practice due to over-squashing, over-smoothing, and finite model capacity.
Binary Characterization: Expressivity theory cannot differentiate between tasks of varying practical difficulty if both are theoretically solvable.
Task and Graph Family Agnosticism: The theory is global, considering all possible graphs and tasks, whereas real-world applications involve restricted graph families and specific tasks.
Empirical Disconnect: Many real-world tasks do not require expressivity beyond the WL test, and empirical performance often does not correlate with theoretical expressivity.

These limitations are illustrated by the inability of expressivity theory to explain why architectural modifications such as virtual nodes, which do not increase expressivity, can dramatically improve performance on long-range tasks.

Message Passing Complexity: Definition and Theoretical Properties

MPC is defined as a continuous measure of the difficulty for a GNN to solve a specific task on a specific graph, given the architecture's message passing scheme. The key innovation is the lossyWL test, a probabilistic variant of the WL test that models the possibility of message loss during propagation. The MPC for a node-level task $f_v$ on graph $G$ is:

$\mathrm{MPC}(f_v, G) = -\log \mathbb{P}[\text{lossyWL}_v^L(G) \vDash f_v(G)]$

where $\vDash$ denotes that the output of the lossyWL process at node $v$ after $L$ layers contains sufficient information to deduce $f_v(G)$ . The probability is computed over the random outcomes of message survival, parameterized by the graph topology and the architecture's message passing graph.

MPC retains all impossibility results from expressivity theory: if a task is theoretically impossible for an architecture, MPC is infinite. However, for feasible tasks, MPC provides a continuous measure of practical difficulty, sensitive to graph structure, task requirements, and architectural choices.

Key theoretical properties:

Subsumes Expressivity Theory: MPC is infinite if and only if the task is impossible for the architecture, recovering all classical impossibility results.
Task Refinement: If $f$ is more fine-grained than $g$ , then $\mathrm{MPC}(f) \geq \mathrm{MPC}(g)$ .
Compositionality: The complexity of solving two tasks jointly is at most the sum of their individual complexities.
Captures Over-squashing and Under-reaching: MPC is lower-bounded by the negative log of the $L$ -step random walk probability between nodes, directly connecting to known bottlenecks in information propagation.

Empirical Validation and Practical Implications

The paper validates MPC across a suite of fundamental GNN tasks, demonstrating that trends in MPC complexity align with empirical performance, while classical expressivity theory fails to do so.

Retaining Node Features and Over-smoothing

The task $f_v(G) = x_v$ (recovering the initial node feature) is trivial in theory but becomes increasingly difficult with depth due to over-smoothing. MPC increases at least linearly with depth, matching the observed drop in accuracy for most architectures, except those with explicit residual connections.

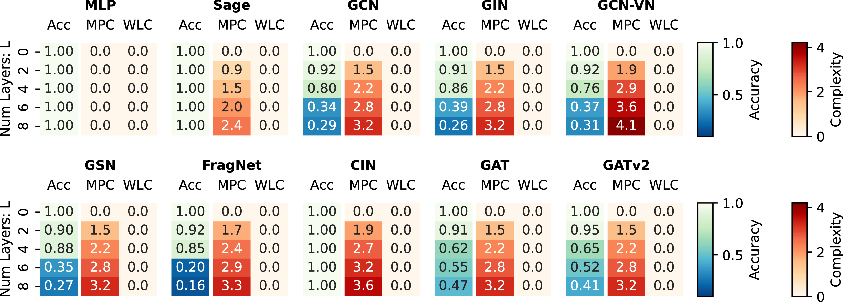
Figure 1: Test accuracy for retaining initial node features compared with complexity measures and WLC for all models. Simulated MPC matches empirical accuracy trends, capturing increasing difficulty with depth.

Information Propagation and Long-range Dependencies

For the task $f_v(G) = x_u$ where $u$ is at distance $D$ from $v$ , MPC increases with $D$ for standard MPNNs, reflecting the empirical failure to propagate information over long distances. Architectures with virtual nodes exhibit dramatically lower MPC, explaining their superior performance despite unchanged expressivity.

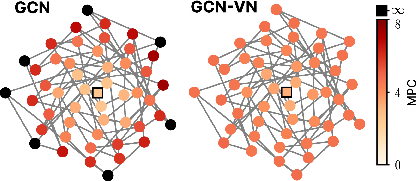
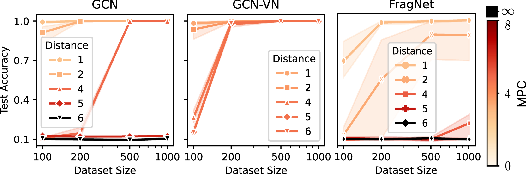
Figure 2: Simulated complexities for propagating features from source nodes $u$ to target node $v$ . Despite identical iso expressivity, MPC reveals the significant advantage virtual nodes offer for long-range dependencies.

Figure 3: Test accuracy by training data size for the information propagation task $f_v(G) = x_u$ for different distances $D$ . Higher MPC values reflect greater task difficulty and increased sample complexity.

Topological Feature Extraction and Cycle Detection

For tasks requiring cycle detection (e.g., identifying all nodes in a cycle containing $v$ ), MPC captures the advantage of architectures with cycle-oriented inductive biases (e.g., CIN, FragNet, GSN), which achieve logarithmic complexity scaling with cycle size, in contrast to the linear scaling for standard MPNNs. This explains empirical performance differences on both synthetic and real-world molecular datasets.

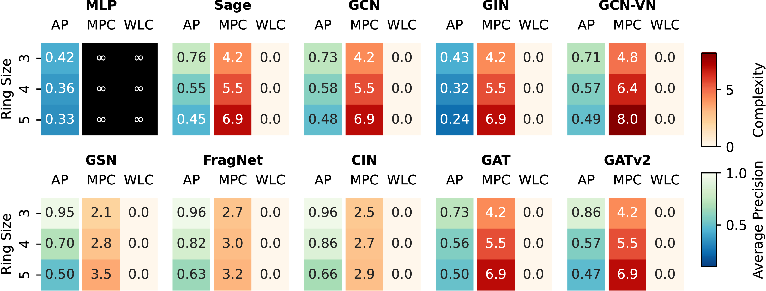
Figure 4: Test average precision for the ring transfer task compared with complexity measures and WLC across all models. MPC aligns with empirical accuracy trends, capturing both the increasing difficulty with ring size and the superior performance of cycle-oriented models.

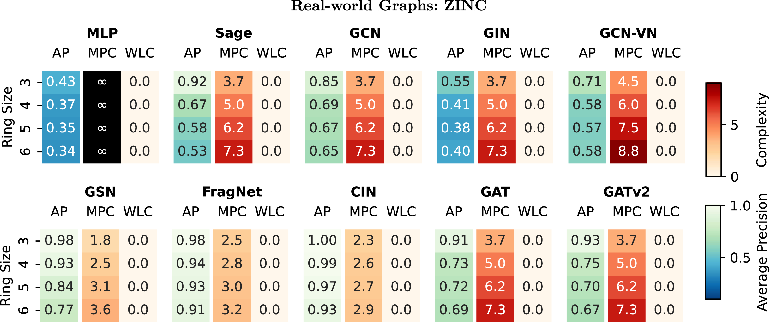
Figure 5: Test average precision compared with complexity measures and WLC for the ring transfer task for real-world graphs from the ZINC dataset. MPC accounts for performance differences that classical expressivity theory misses.

Implementation and Application

Computing MPC

MPC can be estimated via Monte Carlo simulation of the lossyWL process. For a given task and architecture, simulate message passing with probabilistic message loss according to the architecture's message passing graph and edge probabilities. For each trial, check if the output at the target node suffices to deduce the task output. The negative log of the empirical success probability yields the MPC estimate.

import numpy as np

def simulate_mpc(graph, source, target, L, edge_probs, num_trials, task_fn):
    success = 0
    for _ in range(num_trials):
        active = {source}
        for _ in range(L):
            new_active = set()
            for v in active:
                for u in graph.neighbors(v):
                    if np.random.rand() < edge_probs[(v, u)]:
                        new_active.add(u)
            active = new_active
        if target in active and task_fn(graph, source, target):
            success += 1
    return -np.log(success / num_trials)

Architectural Design Guidance

MPC provides actionable guidance for architecture selection and design:

Task-specific Optimization: Rather than maximizing global expressivity, design architectures to minimize MPC for the target task (e.g., add virtual nodes for long-range tasks, use cycle-aware modules for molecular graphs).
Benchmarking and Model Selection: Use MPC to predict which architectures will perform best on a given dataset and task, even when expressivity theory is uninformative.
Proxy Task Analysis: When the exact target function is unknown, analyze proxy tasks (e.g., information retention, cycle detection) to infer architectural suitability.

Scaling and Limitations

Computational Cost: Exact MPC computation is intractable for large graphs and complex tasks; Monte Carlo estimation is practical and sufficient for comparative analysis.
Abstraction Level: MPC abstracts away from parameterization and optimization details, focusing on architectural and topological factors.
Extension to Attention and Feature Noise: The framework can be extended to attention-based models and to incorporate feature noise by modifying the message survival probabilities.

Implications and Future Directions

MPC fundamentally shifts the focus of GNN analysis from maximizing expressivity to minimizing task-specific complexity. This perspective has several implications:

Theoretical: Provides a unified framework that subsumes expressivity theory and incorporates practical limitations, enabling a more nuanced understanding of GNN capabilities.
Practical: Offers a principled basis for architectural innovation, model selection, and benchmarking, directly aligned with empirical performance.
Research Directions: Future work can extend MPC to more complex architectures (e.g., attention, heterogeneous graphs), incorporate additional sources of difficulty (e.g., feature noise), and develop efficient algorithms for MPC estimation in large-scale settings.

Conclusion

Message Passing Complexity (MPC) provides a continuous, task-specific measure of the practical difficulty of solving a given task with a given GNN architecture. By modeling lossy information propagation, MPC captures both theoretical impossibility and practical limitations such as over-squashing and under-reaching, offering a more complete and predictive framework than classical expressivity theory. Empirical validation demonstrates that MPC aligns with observed performance across a range of tasks and architectures, providing actionable insights for GNN design and analysis. This framework encourages a shift from maximizing expressivity to strategically minimizing complexity for domain-relevant tasks, with significant implications for both theory and practice in graph representation learning.