An Introduction to Gravitational Wave Theory (2508.21817v1)

Abstract: Introduction to the theoretical foundations of gravitational waves: from general relativity to detection and binary system waveforms. Lecture notes prepared for the MaNiTou summer school on gravitational waves. Draft chapter for the CNRS contemporary Encyclopaedia Sciences to be published by ISTE.

• The paper presents a rigorous derivation of gravitational wave theory from general relativity, emphasizing gauge structures and observable effects.
• It employs linearized gravity, tensor decompositions, and multipole expansions to isolate the physical degrees of freedom of gravitational waves.
• The study connects theoretical models with astrophysical observations, addressing standard sirens, waveform modeling, and GW memory effects.

An Expert Overview of "An Introduction to Gravitational Wave Theory" (2508.21817)

Introduction and Scope

"An Introduction to Gravitational Wave Theory" provides a comprehensive and technically rigorous exposition of the theoretical underpinnings of gravitational waves (GWs), from their emergence in general relativity (GR) to their detection and astrophysical implications. The text systematically develops the subject, beginning with the conceptual and mathematical structure of GR, progressing through the linearized theory and gauge structure, and culminating in the detailed modeling of GW sources, propagation, and detection. The treatment is notable for its explicit attention to gauge subtleties, the role of symmetries, and the connection between theoretical constructs and experimental observables.

General Covariance, Gauge Structure, and Noether Charges

The paper begins by emphasizing the foundational role of general covariance in GR, highlighting the distinction between proper and gauge symmetries via Noether's theorem. The analysis of the Einstein-Hilbert action and its invariance under diffeomorphisms is used to clarify the status of coordinate transformations as gauge redundancies, except in the presence of isometries, where nontrivial Noether charges (e.g., Komar charges) arise. The discussion of asymptotic symmetries, including the BMS group at null infinity, is particularly relevant for the nonperturbative understanding of GW energy and memory effects.

Linearized Gravity and Physical Degrees of Freedom

The weak-field (linearized) approximation is developed in detail, with a careful decomposition of the metric perturbation $h_{\mu\nu}$ into irreducible spin and helicity components under the Lorentz group. The analysis demonstrates that, after gauge fixing (notably in the transverse-traceless (TT) gauge), only two physical, gauge-invariant degrees of freedom remain, corresponding to the two GW polarizations with helicity $\pm2$. The explicit construction of the TT projector and the identification of the physical content of the metric perturbation are presented with full tensorial rigor.

The gauge structure is further elucidated by contrasting the De Donder (harmonic) gauge, temporal gauge, and Coulomb gauge, and by showing how the residual gauge freedom is handled in the presence of sources. The treatment of the gauge-invariant potentials (e.g., $\Phi$, $\Psi$) and their relation to the Newtonian and post-Newtonian limits is precise and connects directly to observable effects.

Generation and Propagation of Gravitational Waves

The derivation of the quadrupole formula for GW emission is presented via a systematic multipole expansion, with explicit expressions for the leading and subleading contributions. The absence of monopole and dipole radiation is shown to follow from conservation laws, and the explicit dependence of the GW amplitude on the source's quadrupole moment and its derivatives is given. The scaling of the GW amplitude and the detection horizon for various source classes (BNS, BBH, MBHB) are quantitatively established.

The propagation of GWs in curved backgrounds, particularly in cosmological (FRLW) spacetimes, is treated using the WKB approximation. The analysis demonstrates the redshifting of GW frequencies and the $1/a$ damping of amplitudes, leading to the identification of the luminosity distance as the relevant observable for GW standard sirens. The degeneracy between redshifted and source-frame masses in GW observations is highlighted, with implications for cosmological parameter inference.

Detection Principles and Experimental Realizations

The physical effect of GWs on test masses is derived from the geodesic deviation equation, with a clear distinction between coordinate and physical displacements. The response of laser interferometers is computed in the long-wavelength approximation, and the detector pattern functions for the two GW polarizations are given explicitly. The necessity of multiple detectors for polarization disentanglement and source localization is emphasized.

Figure 1: The tidal deformation of a ring of test masses under the action of the two GW polarizations, $h_+$ and $h_\times$, illustrating the quadrupolar nature of the interaction.

Astrophysical Sources: Compact Binaries and Memory Effects

The modeling of compact binary coalescences (CBCs) is developed from Newtonian dynamics through the post-Newtonian regime, with explicit analytic expressions for the GW waveforms in both circular and eccentric orbits. The secular evolution of orbital elements under GW backreaction is derived, including the classic Peters-Mathews formula for eccentricity damping. The frequency content of GW signals from eccentric binaries is analyzed via Fourier decomposition, revealing the distribution of power among harmonics.

The treatment of unbound (hyperbolic) encounters is notable for its explicit calculation of the linear GW memory effect, with analytic expressions for the permanent displacement induced in a GW detector. The connection between the low-frequency limit of the GW spectrum and the memory effect is made explicit.

Geometric Aspects: Source-Observer Geometry

The transformation between the source frame and the observer frame is handled via explicit rotations, with the orientation of the binary's orbital plane relative to the line of sight parameterized by inclination and node angles.

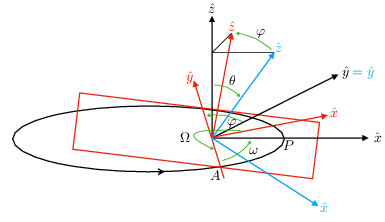
Figure 2: The sequence of rotations relating the binary's orbital plane to the observer's frame, defining the inclination and node angles relevant for waveform modeling.

Conservation Laws and Energy Flux

The derivation of the GW energy and angular momentum fluxes is performed using the Isaacson stress-energy tensor, with careful attention to gauge invariance and the limitations imposed by the equivalence principle. The global conservation laws are connected to the asymptotic structure of spacetime, and the role of averaging procedures in defining meaningful energy densities is discussed.

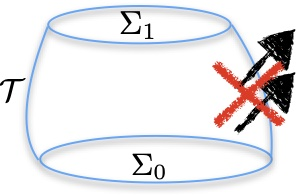
Figure 3: Schematic of a spacetime region bounded by spacelike and timelike hypersurfaces, illustrating the application of conservation laws and the role of boundary terms in the presence of Killing symmetries.

Cosmological Implications and Standard Sirens

The propagation of GWs over cosmological distances is analyzed, with the explicit demonstration that GW observations provide direct measurements of the luminosity distance, independent of the cosmic distance ladder. The degeneracy between redshift and source-frame masses is shown to be a fundamental limitation for GW-only cosmology, unless electromagnetic counterparts or additional waveform features (e.g., tidal effects in BNS) are available. The use of GW standard sirens for $H_0$ inference is discussed, with reference to the GW170817 event and the prospects for future population-based constraints.

Theoretical and Practical Implications

The text provides a robust foundation for both theoretical investigations and practical data analysis in GW astrophysics. The explicit treatment of gauge issues, the connection between symmetries and observables, and the detailed modeling of source dynamics are all essential for the interpretation of GW signals and the extraction of physical parameters. The discussion of memory effects and their detectability with current and future detectors points to ongoing and future research directions, including the exploitation of GW observations for fundamental tests of gravity and cosmology.

Conclusion

"An Introduction to Gravitational Wave Theory" offers a technically complete and conceptually clear account of the theory of GWs, suitable for advanced researchers seeking a rigorous understanding of both foundational and applied aspects. The explicit attention to gauge structure, symmetries, and the connection between theory and experiment ensures the utility of the text for both theoretical development and the interpretation of observational data. The inclusion of detailed derivations, analytic results, and geometric visualizations (as in Figures 4, 5, and 7) enhances the pedagogical and practical value of the work. The framework established here is directly relevant for ongoing developments in GW astronomy, including the modeling of complex sources, the analysis of memory effects, and the use of GWs as cosmological probes.