QR-LoRA: QR-Based Low-Rank Adaptation for Efficient Fine-Tuning of Large Language Models (2508.21810v1)

Abstract: The growing scale of LLMs has necessitated the development of parameter-efficient fine-tuning techniques. Low-Rank Adaptation (LoRA) has emerged as a promising approach, reducing the number of trainable parameters by applying low-rank updates to pretrained weights. While standard LoRA learns both update factors directly, several recent variants first initialize those matrices via an SVD of the pretrained weights -- an operation that can be expensive on large models and yields singular vectors that are not always easy to interpret. In this work, we extract an orthonormal basis from the pretrained weight matrix using QR decomposition with column pivoting, and then express the LoRA update as a linear combination of these basis vectors -- training only the scalar coefficients, which imposes clear structure on adaptation and drastically reduces parameter count. Experiments across GLUE tasks show that QR-LoRA matches or exceeds the performance of full fine-tuning, standard LoRA, and SVD-LoRA (LoRA with update matrices initialized via singular value decomposition) with as few as 601 parameters -- a reduction of over 1000x compared to full fine-tuning and 77x fewer than typical LoRA setups.

• The paper introduces a QR-based low-rank adaptation method that uses pivoted QR decomposition to extract an interpretable orthonormal basis for efficient LLM fine-tuning.
• It demonstrates that QR-LoRA achieves competitive performance on benchmark tasks with 77×–153× fewer parameters than full fine-tuning.
• The approach offers improved numerical stability and regularization, making it well-suited for resource-constrained deployments and large-scale adaptation.

QR-LoRA: QR-Based Low-Rank Adaptation for Efficient Fine-Tuning of LLMs

Introduction and Motivation

The QR-LoRA method addresses the challenge of parameter-efficient fine-tuning for LLMs, where updating the full parameter set is computationally prohibitive. Existing adapter-based approaches, such as LoRA, reduce the number of trainable parameters by learning low-rank updates to frozen weights. However, variants that rely on SVD initialization incur significant computational cost and lack interpretability in the basis selection. QR-LoRA introduces a pivoted QR decomposition to extract an orthonormal basis from pretrained weights, enabling highly structured and interpretable adaptation with minimal trainable parameters.

Methodology: QR-Based Low-Rank Adaptation

QR-LoRA modifies the standard LoRA update by leveraging the QR decomposition with column pivoting. For a given pretrained weight matrix $W_0 \in \mathbb{R}^{L \times M}$, the pivoted QR decomposition yields $W_0 = Q R$, where $Q$ is orthonormal and $R$ is upper triangular with diagonal entries ordered by magnitude. The update is parameterized as:

$\Delta W = \sum_{i=1}^{r} \lambda_i Q_i R_i^T$

where $Q_i$ is the $i$-th column of $Q$, $R_i^T$ is the transposed $i$-th row of $R$, and $\lambda_i$ are trainable scalars. The rank $r$ is selected to capture a specified fraction $\tau$ of the cumulative energy in $R$'s diagonal, typically $90$–$95\%$. This approach fixes the adaptation subspace and only tunes the scalar coefficients, drastically reducing the number of trainable parameters.

The orthonormality of $Q$ ensures non-redundant, independent update directions, improving numerical stability and regularization. The pivoted QR decomposition provides a natural importance ordering, facilitating principled rank selection and interpretability. Compared to SVD-based methods, QR decomposition is computationally efficient and scalable to large matrices.

Experimental Results

QR-LoRA was evaluated on eight GLUE benchmark tasks using RoBERTa-base as the backbone. The method was compared against full fine-tuning, standard LoRA, and SVD-LoRA. QR-LoRA configurations varied the threshold $\tau$, the number of layers adapted, and the set of projection matrices ($W_q$, $W_v$, $W_o$) targeted.

Across MNLI and MRPC, QR-LoRA achieved matched and mismatched accuracies of up to $82.07\%$ and $82.29\%$ on MNLI, and an F1 score of $92.15\%$ on MRPC, with as few as $614$ trainable parameters. These results are within $0.1$–$0.3$ percentage points of, and in some cases surpass, the full fine-tuning baseline (125M parameters). QR-LoRA consistently outperformed SVD-LoRA and matched or exceeded standard LoRA, despite using $77\times$–$153\times$ fewer parameters.

The parameter-performance trade-off is visualized in the following figure, which demonstrates that QR-LoRA occupies the optimal region of high accuracy and low parameter count.

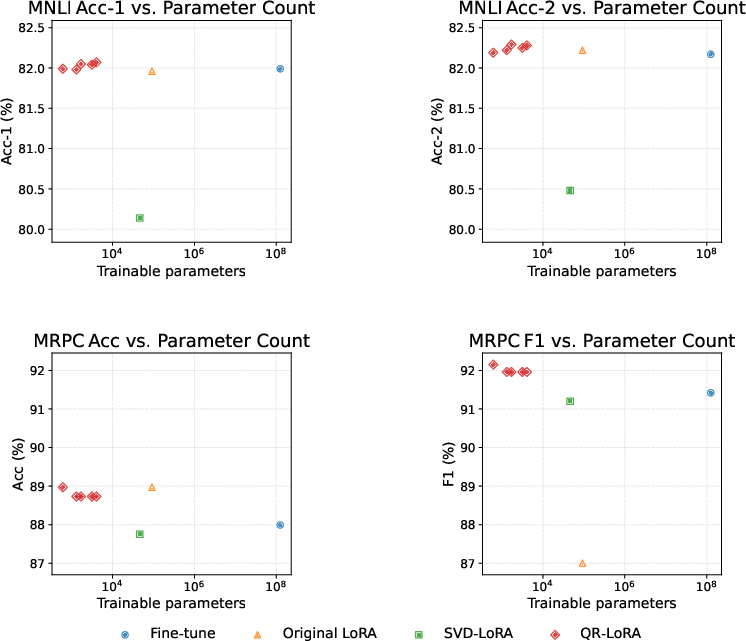
Figure 1: Effect of trainable parameter count on downstream performance. Top row: MNLI matched (left) and mismatched (right) accuracy; bottom row: MRPC accuracy (left) and F1 (right), for Fine-tune, Original LoRA, SVD-LoRA and QR-LoRA variants.

Ablation studies on training set size revealed that QR-LoRA is most advantageous in moderate- to high-resource regimes. With small datasets (e.g., 2,000 examples), full fine-tuning outperformed QR-LoRA, but as the dataset size increased, QR-LoRA matched or exceeded full fine-tuning performance. This suggests that the strong regularization induced by the fixed orthonormal subspace is beneficial when sufficient data is available.

On the RTE task, QR-LoRA and other adapter methods underperformed relative to full fine-tuning, likely due to the small dataset size and the need for more flexible adaptation in low-resource, out-of-distribution settings.

Implementation Considerations

Implementing QR-LoRA requires only a single pivoted QR decomposition per weight matrix, which is computationally efficient and can be performed with standard linear algebra libraries (e.g., LAPACK, SciPy). The selection of the threshold $\tau$ directly controls the rank and thus the number of trainable parameters. The method is robust to hyperparameter choices, with marginal performance differences observed across variations in $\tau$, layer selection, and projection matrices adapted.

For practical deployment, QR-LoRA is well-suited to resource-constrained environments, such as on-device personalization, where minimizing storage and compute is critical. The fixed adaptation subspace also facilitates interpretability and analysis of the learned directions.

Theoretical Implications

QR-LoRA connects to the literature on intrinsic dimension in neural network fine-tuning, where restricting updates to low-dimensional subspaces improves generalization. The use of an orthonormal basis aligns with principles from numerical linear algebra, ensuring stable optimization and efficient representation. The method provides a structured framework for parameter-efficient adaptation, with clear theoretical motivation and practical benefits.

Future Directions

Potential extensions of QR-LoRA include:

• Application to other layer types (e.g., feed-forward networks, embeddings, output heads).
• Evaluation on more challenging benchmarks (e.g., SuperGLUE, generation tasks).
• Adaptation to decoder-only architectures and multimodal models.
• Integration with dynamic rank selection or adaptive thresholding for further efficiency gains.

Exploring the limits of QR-LoRA in extreme low-resource and distribution-shifted settings remains an open question.

Conclusion

QR-LoRA introduces a principled, efficient approach to low-rank adaptation for LLM fine-tuning, leveraging pivoted QR decomposition to extract an interpretable, orthonormal basis for updates. The method achieves competitive or superior performance to full fine-tuning and existing adapter methods with orders of magnitude fewer trainable parameters. QR-LoRA is robust, scalable, and well-motivated both theoretically and practically, representing a significant advance in parameter-efficient model adaptation.