A-MHA*: Anytime Multi-Heuristic A* (2508.21637v1)

Abstract: Designing good heuristic functions for graph search requires adequate domain knowledge. It is often easy to design heuristics that perform well and correlate with the underlying true cost-to-go values in certain parts of the search space but these may not be admissible throughout the domain thereby affecting the optimality guarantees of the search. Bounded suboptimal search using several such partially good but inadmissible heuristics was developed in Multi-Heuristic A* (MHA*). Although MHA* leverages multiple inadmissible heuristics to potentially generate a faster suboptimal solution, the original version does not improve the solution over time. It is a one shot algorithm that requires careful setting of inflation factors to obtain a desired one time solution. In this work, we tackle this issue by extending MHA* to an anytime version that finds a feasible suboptimal solution quickly and continually improves it until time runs out. Our work is inspired from the Anytime Repairing A* (ARA*) algorithm. We prove that our precise adaptation of ARA* concepts in the MHA* framework preserves the original suboptimal and completeness guarantees and enhances MHA* to perform in an anytime fashion. Furthermore, we report the performance of A-MHA* in 3-D path planning domain and sliding tiles puzzle and compare against MHA* and other anytime algorithms.

• The paper introduces A-MHA*, an anytime extension of MHA* that integrates iterative improvement to provide rapid, bounded suboptimal solutions.
• It employs multiple priority queues with dual inflation factors to balance the speed of initial solution discovery with continuous, monotonic refinement.
• Empirical evaluations on 3D path planning and sliding tile puzzles show superior initial performance and convergence compared to traditional methods.

Anytime Multi-Heuristic A*: An Anytime Extension of MHA*

Introduction

The paper introduces A-MHA*, an anytime extension of the Multi-Heuristic A* (MHA*) algorithm, designed to address the limitations of one-shot bounded suboptimal search in high-dimensional planning domains. MHA* leverages multiple heuristics—one admissible and several potentially inadmissible—to accelerate search, but requires a priori specification of suboptimality bounds and does not improve solutions over time. A-MHA* integrates the iterative improvement paradigm of Anytime Repairing A* (ARA*) into the MHA* framework, enabling rapid initial solution generation followed by continuous refinement, while maintaining theoretical guarantees on completeness and suboptimality.

Algorithmic Framework

A-MHA* operates over a discrete state space $\mathcal{S}$, searching for a path from $s_{start}$ to $s_{goal}$. The algorithm maintains $N+1$ priority queues: one for the anchor (admissible) heuristic and $N$ for the inadmissible heuristics. Each queue orders states by a key function $key(s, i) = g(s) + w_1 h_i(s)$, where $g(s)$ is the current cost-to-come, $h_i(s)$ is the $i$-th heuristic, and $w_1$ is the inflation factor for the anchor search. Inadmissible searches are further prioritized by a secondary inflation factor $w_2$.

The core of A-MHA* is an outer loop that iteratively calls an \textproc{ImprovePath()} routine, each time with reduced inflation factors, thereby tightening the suboptimality bound. The algorithm maintains two closed lists (for anchor and inadmissible searches) and a single inconsistent list (INCONS) to track states whose $g$-values have improved after expansion, following the local inconsistency propagation strategy of ARA*.

The expansion policy ensures that, within each \textproc{ImprovePath()} call, a state is expanded at most twice—once by the anchor search and once by an inadmissible search. After each improvement iteration, all inconsistent states are reinserted into the open lists, and the inflation factors are decremented, guaranteeing monotonic improvement of the solution.

Theoretical Properties

A-MHA* preserves the key theoretical properties of both MHA* and ARA*:

• Bounded Suboptimality: At the end of each \textproc{ImprovePath()} call, the solution cost is guaranteed to be at most $w_1 w_2$ times the optimal cost. This is achieved by restricting expansions in the inadmissible searches to states whose priority does not exceed $w_2$ times the minimum anchor key.
• Completeness: The algorithm is complete for finite graphs, as it systematically explores all reachable states under the given heuristics.
• Expansion Bound: Each state is expanded at most twice per improvement iteration, ensuring efficient use of computational resources.

Experimental Evaluation

A-MHA* is empirically evaluated on two domains: 3D path planning for a nonholonomic robot and large sliding tile puzzles. In both cases, the algorithm is compared against MHA*, ARA*, and ANA*.

3D Path Planning

In the 3D planning domain, the robot operates in a planar environment with $(x, y, \theta)$ state space and minimum turning radius constraints. The anchor heuristic is Euclidean distance, while inadmissible heuristics include Dijkstra-based estimates with varying map modifications.

A-MHA* demonstrates rapid initial solution generation and continuous improvement, outperforming other algorithms in early solution quality and convergence rate.

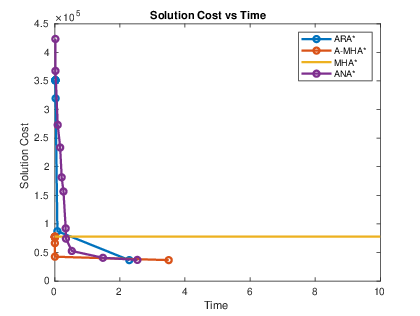
Figure 1: Solution cost as a function of time for 3D planning, showing A-MHA

's rapid initial solution and subsequent improvement.*

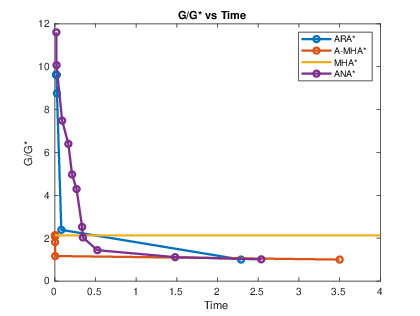
Figure 2: Suboptimality of the solution versus time for 3D planning, illustrating the monotonic reduction in suboptimality by A-MHA

compared to baselines.*

The results indicate that A-MHA* produces high-quality solutions significantly faster than ARA* and ANA*, with the caveat that the use of inadmissible heuristics can delay convergence to true optimality.

Sliding Tile Puzzle

For the 48- and 63-tile sliding puzzle, the anchor heuristic is the sum of Manhattan Distance and Linear Conflict, while inadmissible heuristics are weighted combinations of standard puzzle heuristics with randomized weights.

A-MHA* achieves the highest success rate and fastest initial solution times for the 63-tile puzzle, with final suboptimality bounds superior to ARA* and ANA*. For the 48-tile puzzle, A-MHA* and ARA* perform comparably, suggesting that the benefit of multiple heuristics is more pronounced in larger, more complex state spaces.

Practical and Theoretical Implications

A-MHA* provides a principled approach for integrating multiple heuristics—regardless of admissibility—into an anytime search framework. This is particularly valuable in domains where designing globally admissible heuristics is infeasible, but informative local heuristics are available. The algorithm's ability to rapidly produce feasible solutions and iteratively improve them is well-suited for real-time robotic planning, high-dimensional motion planning, and combinatorial puzzles.

The main trade-off is that while inadmissible heuristics accelerate initial solution discovery, they can slow convergence to optimality. The need to tune two inflation parameters ($w_1$, $w_2$) introduces additional complexity, though the authors suggest future work on nonparametric adaptation.

Future Directions

Potential avenues for further research include:

• Adaptive Inflation Scheduling: Automatically adjusting $w_1$ and $w_2$ based on observed search progress or solution quality, reducing the need for manual parameter tuning.
• Heuristic Selection: Dynamic selection or weighting of heuristics during search to maximize informativeness and minimize overhead.
• Parallelization: Exploiting the independence of multiple heuristic searches for parallel or distributed implementations.
• Application to Continuous Domains: Extending A-MHA* to kinodynamic or continuous state spaces, where heuristic design is even more challenging.

Conclusion

A-MHA* successfully extends the MHA* framework to the anytime setting, combining the strengths of multi-heuristic search and iterative solution improvement. The algorithm maintains strong theoretical guarantees and demonstrates superior empirical performance in complex planning domains. Its design is particularly advantageous in scenarios where multiple informative but inadmissible heuristics are available, and rapid, progressively improving solutions are required.