PVPO: Pre-Estimated Value-Based Policy Optimization for Agentic Reasoning (2508.21104v1)

Abstract: Critic-free reinforcement learning methods, particularly group policies, have attracted considerable attention for their efficiency in complex tasks. However, these methods rely heavily on multiple sampling and comparisons within the policy to estimate advantage, which may cause the policy to fall into local optimum and increase computational cost. To address these issues, we propose PVPO, an efficient reinforcement learning method enhanced by an advantage reference anchor and data pre-sampling. Specifically, we use the reference model to rollout in advance and employ the calculated reward score as a reference anchor. Our approach effectively corrects the cumulative bias introduced by intra-group comparisons and significantly reduces reliance on the number of rollouts. Meanwhile, the reference model can assess sample difficulty during data pre-sampling, enabling effective selection of high-gain data to improve training efficiency. Experiments conducted on nine datasets across two domains demonstrate that PVPO achieves State-Of-The-Art (SOTA) performance. Our approach not only demonstrates robust generalization across multiple tasks, but also exhibits scalable performance across models of varying scales.

• The paper presents PVPO, a critic-free RL method that decouples dynamic Q and static V estimates to deliver stable, low-variance policy updates.
• It employs a group sampling strategy to filter training data, thereby accelerating convergence and reducing computational cost by up to 2.5×.
• Empirical results on multi-hop QA and mathematical reasoning tasks demonstrate significant performance gains over methods like GRPO.

PVPO: Pre-Estimated Value-Based Policy Optimization for Agentic Reasoning

Introduction and Motivation

The PVPO framework introduces a novel critic-free reinforcement learning (RL) algorithm tailored for agentic reasoning tasks, particularly those characterized by sparse rewards and complex multi-step trajectories. Traditional actor-critic methods, such as PPO, rely on a critic network to estimate state values, which incurs substantial computational overhead and instability in large-scale LLM training. Critic-free group policy methods, e.g., GRPO, mitigate resource consumption by estimating advantage via intra-group reward comparisons, but suffer from local optima and require extensive sampling to stabilize training. PVPO addresses these limitations by introducing a static reference anchor for advantage estimation and a group sampling strategy for efficient data selection.

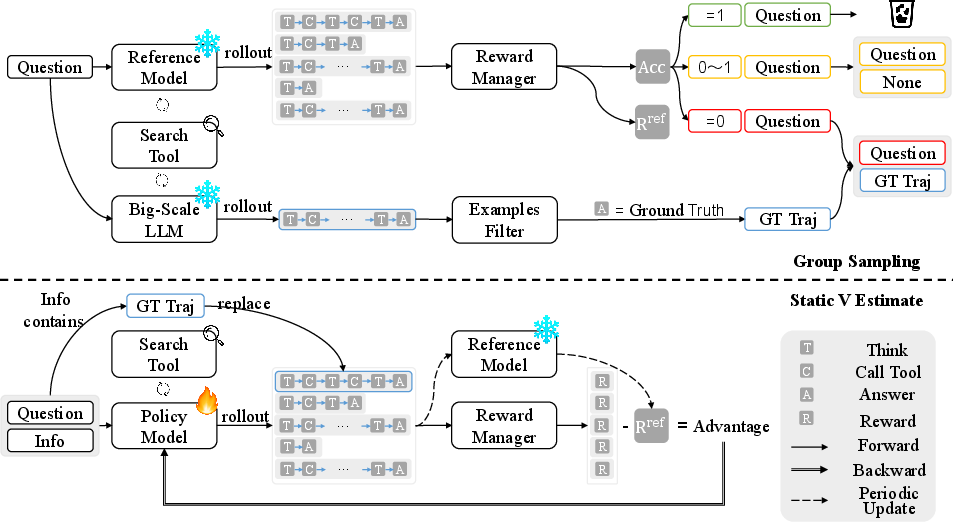
Figure 1: The architecture of PVPO. Reference model updates $R^{\text{ref}}$ at fixed steps, maintaining value stability and improving the performance lower bound.

Methodology

Static V Estimate and Advantage Calculation

PVPO decouples the advantage function into a dynamic $Q$ (on-policy reward) and a static $V$ (reference anchor), where the static $V$ is computed by rolling out a fixed reference model $\pi_{\text{ref}}$ on the training data. This reference anchor is periodically updated and provides a stable, low-variance baseline for advantage calculation, independent of the current policy. The advantage for each trajectory $\tau_i$ is given by:

$$\hat{A}^{\text{PVPO}}(\tau_i, s_0) = r_i - \text{mean}(\mathbf{r}^{\text{ref}})$$

where $r_i$ is the reward from the current policy and $\mathbf{r}^{\text{ref}}$ are rewards from the reference model. This formulation ensures that policy updates are guided by a consistent external baseline, mitigating error accumulation and policy drift.

Group Sampling Strategy

PVPO employs a group sampling mechanism to filter training data based on rollout accuracy. Samples with mean accuracy of 1 (trivial) are excluded, those with accuracy strictly between 0 and 1 are retained, and samples with mean accuracy 0 are further evaluated using a larger LLM to generate ground-truth trajectories (GT Traj). These GT Traj are injected into training batches to provide explicit demonstrations for hard cases, alleviating the sparse reward problem and accelerating learning.

Experimental Results

Multi-Hop Question Answering

PVPO was evaluated on four multi-step retrieval datasets (Musique, 2WikiMultiHopQA, HotpotQA, Bamboogle) using Qwen2.5-7B-Instruct as the base model. PVPO achieved substantial improvements over both zero-shot LLM baselines and agentic retrieval methods trained with GRPO. Specifically, PVPO outperformed GRPO by more than 5 percentage points on average and exceeded the best-performing general LLMs on in-domain datasets.

Mathematical Reasoning

On five mathematical reasoning datasets (MATH500, AMC23, Olympiad, AIME-2024, AIME-2025), PVPO consistently outperformed GRPO across both 7B and 14B model scales, with gains of 1.89 and 1.24 percentage points in average accuracy, respectively. This demonstrates PVPO's robust generalization across domains and model sizes.

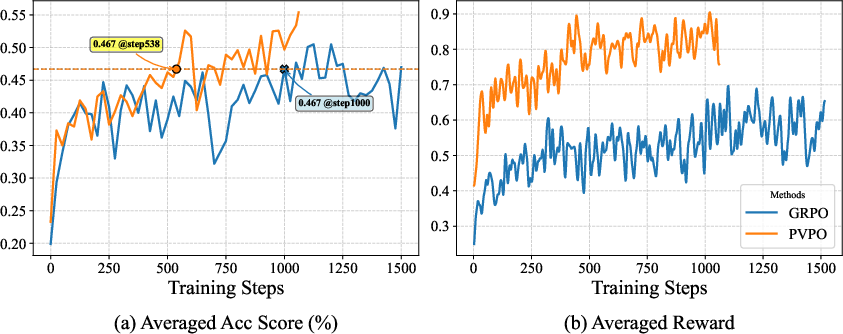
Figure 2: Training efficiency paper of PVPO on mathematical reasoning datasets.

Training Efficiency and Resource Consumption

PVPO converges significantly faster than GRPO, reaching target accuracy in half the training steps. Group sampling filters out 40–60% of the dataset, resulting in a 1.7–2.5$\times$ increase in training speed without sacrificing performance. The static advantage baseline enables efficient policy updates with fewer rollouts, reducing computational cost.

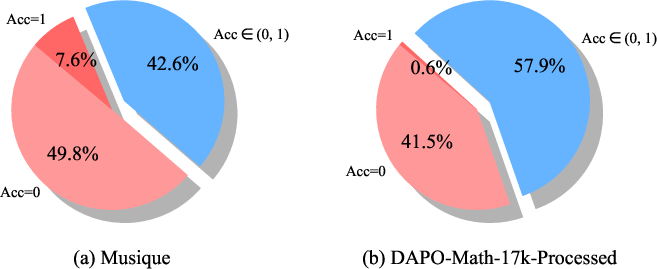
Figure 3: Group Sampling paper on datasets from different fields. The Acc is the mean of the answer accuracies from M trajectories rolled out by the reference model. M=5 in Figure (a) and M=16 in Figure (b).

Training Stability

PVPO exhibits superior training stability, maintaining higher average rewards, lower advantage variance, and greater policy entropy under similar KL constraints compared to GRPO. This results in more reliable gradient directions and prevents premature convergence to suboptimal policies.

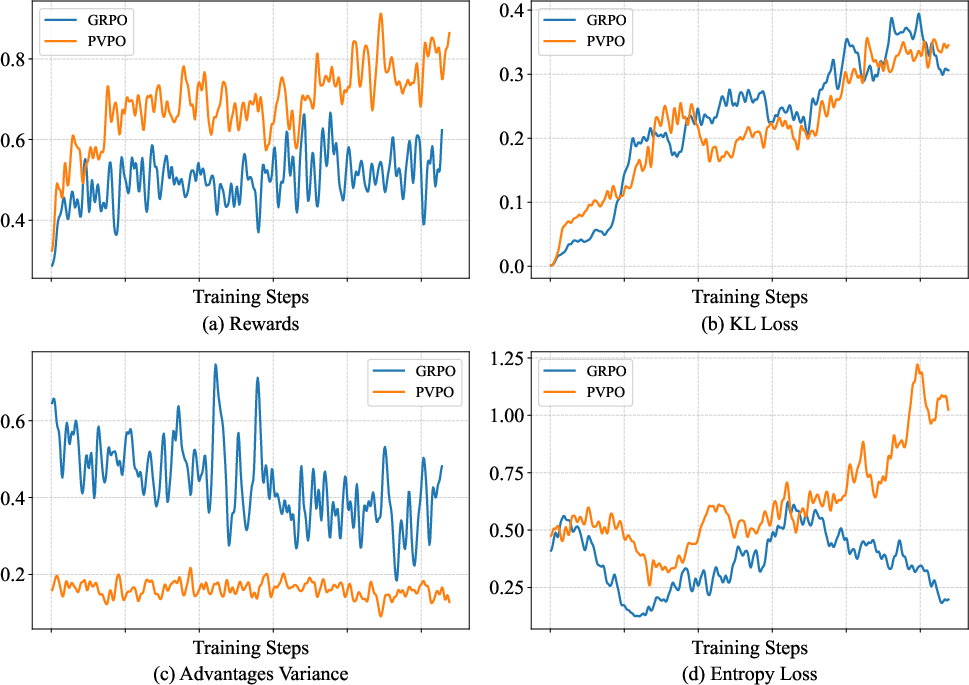
Figure 4: Training stability paper of PVPO on multi-step retrieval datasets.

Low Sampling Budget Case Study

PVPO maintains competitive performance under reduced rollout budgets, achieving 97% of GRPO's accuracy with less than 40% of the computational cost. This strong sample efficiency is attributed to the high-quality, low-variance training signals provided by the static reference anchor.

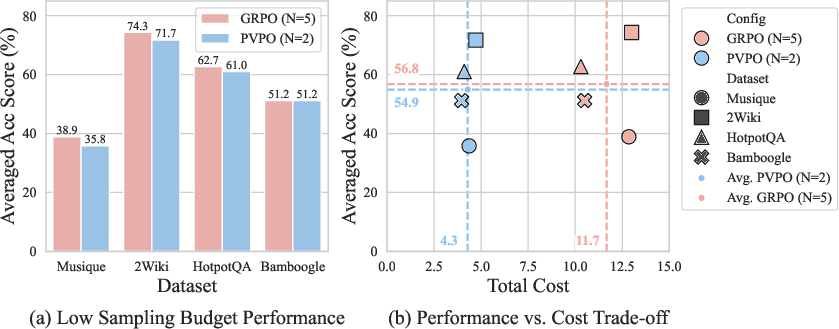
Figure 5: Low sampling budget paper of PVPO on multi-step retrieval datasets. The N denotes the number of trajectories in each single rollout. N=5 is the full budget and N=2 is the low budget.

Implementation Considerations

PVPO is compatible with mainstream RL frameworks for LLMs, such as ReSearch and veRL. The reference model can be any fixed policy, typically the initial checkpoint, and is updated at fixed intervals (e.g., every 500 steps). The number of reference rollouts $M$ should match the policy rollouts $N$ for consistent baseline estimation. Group sampling requires a single offline inference pass, incurring minimal overhead relative to training. PVPO is particularly effective in sparse-reward settings and scales efficiently to larger models and datasets.

Implications and Future Directions

PVPO's critic-free architecture and static advantage baseline offer a principled solution to the instability and resource demands of RL for LLMs. The method is broadly applicable to agentic reasoning, multi-hop retrieval, and mathematical problem solving, and is well-suited for deployment in resource-constrained environments. Future work may explore adaptive reference model selection, integration with offline RL datasets, and extension to multi-agent or hierarchical policy optimization scenarios. The group sampling strategy could be further refined to incorporate curriculum learning or active data selection.

Conclusion

PVPO presents an efficient and generalizable RL algorithm for agentic reasoning, leveraging a static reference anchor and group sampling to deliver stable, low-variance training signals and accelerated convergence. Extensive empirical results demonstrate state-of-the-art performance and strong generalization across diverse tasks and model scales. PVPO's design principles and empirical strengths position it as a robust foundation for future research and practical deployment in RL-driven LLM applications.