Spectral density characteristics of self-organized structuring in phase-synchronized oscillator ensembles (2508.21012v1)

Abstract: Self-organized turbulence represents a way for structuring in nature to arise through sheer complexity rather than through linear instability theory. Simulating ensembles of oscillators that undergo phase synchronization through a propagating Kuramoto-interaction field, we present the spectral characteristics of spontaneous, self-organized structures of locally coupled oscillators. We demonstrate that the spectral density of emergent structures can exhibit universal scaling laws, in line with expectations from nature, indicating that observed statistical outcomes of complex physical interactions can be achieved through a more general principle of self-organization. We suggest that spontaneously generated structures may provide nuance to the reigning reductionist explanations for the observed structure in coupled systems of astrophysical and geophysical plasmas.

• The paper demonstrates that universal spectral density scaling laws emerge in locally coupled oscillator ensembles through self-organization and phase synchronization.
• Simulations reveal that spectral indices stabilize between -2.32 and -2.67, indicating robust turbulent energy transfer in both fast and slow natural frequency modes.
• Results suggest that macroscopic structuring in complex systems may originate from generic self-organization, mirroring turbulent patterns observed in astrophysical plasmas.

Spectral Density and Self-Organization in Phase-Synchronized Oscillator Ensembles

Introduction

This paper investigates the emergence of universal spectral density scaling laws in ensembles of locally coupled oscillators subject to phase synchronization via a propagating Kuramoto field. The paper is motivated by the need to understand the origin of macroscopic structuring in turbulent systems, particularly in astrophysical and geophysical plasmas, where reductionist approaches often fail to account for observed universal statistical outcomes. The work builds on the theoretical foundation of locally coupled Kuramoto models and explores the role of self-organization in generating dissipative structures with characteristic spectral indices.

Simulation Framework and Methodology

The simulation models $N=30,000$ oscillators in a two-dimensional periodic domain, each characterized by a position vector $\mathbf{x}_k$ and an internal phase $\phi_k$. The velocity of each oscillator is determined by its phase, and the initial conditions are maximally entropic, with positions and phases drawn from uniform random distributions. Natural frequencies $\omega_k$ are sampled from multi-slope power-law distributions to represent a broad spectrum of physical modes.

Phase evolution is governed by a discretized, driven, stochastic Kuramoto-like equation:

$$\phi_k(t+\Delta t) = \phi_k(t) + \left[ \omega_k - A_0H(t) A_{\text{local}}(t) \sin(\phi_k(t) - \Psi_{\text{local}}(t)) + \xi_k(t) \right] \Delta t$$

where $A_0$ is the base coupling strength, $H(t)$ is a Heaviside step function controlling the onset of coupling, $A_{\text{local}}(t)$ and $\Psi_{\text{local}}(t)$ are the amplitude and phase of the local mean field, and $\xi_k(t)$ is Gaussian white noise. The local mean field is computed via a 2D convolution with a pill-box kernel, modeling sharp, local interactions.

Spatial clustering and phase synchronization are amplified through velocity alignment, creating a non-linear feedback loop that drives the formation of large-scale coherent structures. The system is open and non-equilibrium, with coupling strength abruptly increased to trigger phase transitions.

Emergence of Structure and Spectral Analysis

The simulation demonstrates the spontaneous emergence of vortices and filamentary structures from initially chaotic states, as shown in the temporal evolution of the oscillator ensemble.

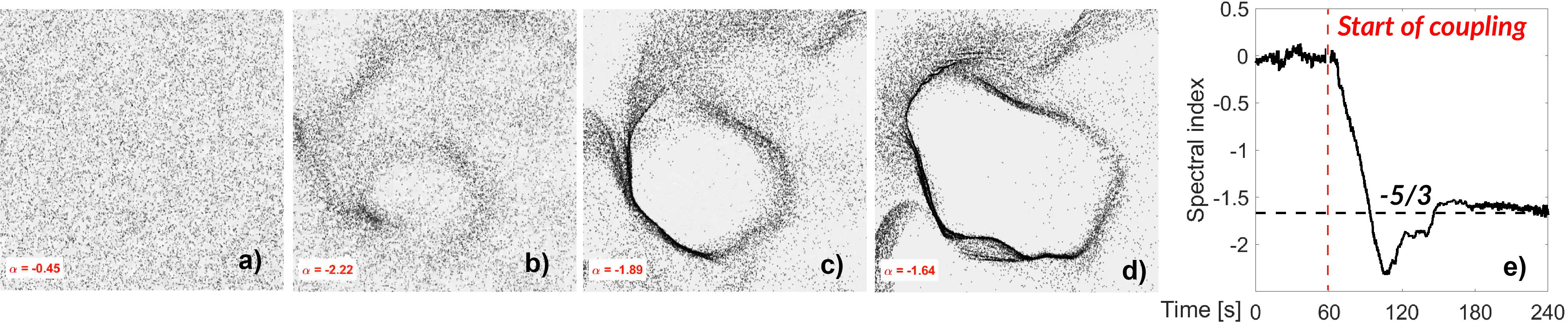
Figure 1: Simulation frames showing the emergence of a vortex and the temporal development of the spectral index $\alpha$ following the onset of coupling.

Spectral analysis is performed by binning oscillator positions onto a $64\times64$ grid and computing the 2D FFT, followed by azimuthal averaging to obtain the 1D spatial power spectrum $P(k)$. The log-log slope of $P(k)$, denoted as the spectral index $\alpha$, quantifies the geometry and energy transfer characteristics of the emergent turbulence.

Results: Universal Scaling Laws

Simulations with different natural frequency distributions ("fast" and "slow" modes) reveal distinct spatial organizations and phase evolution patterns.

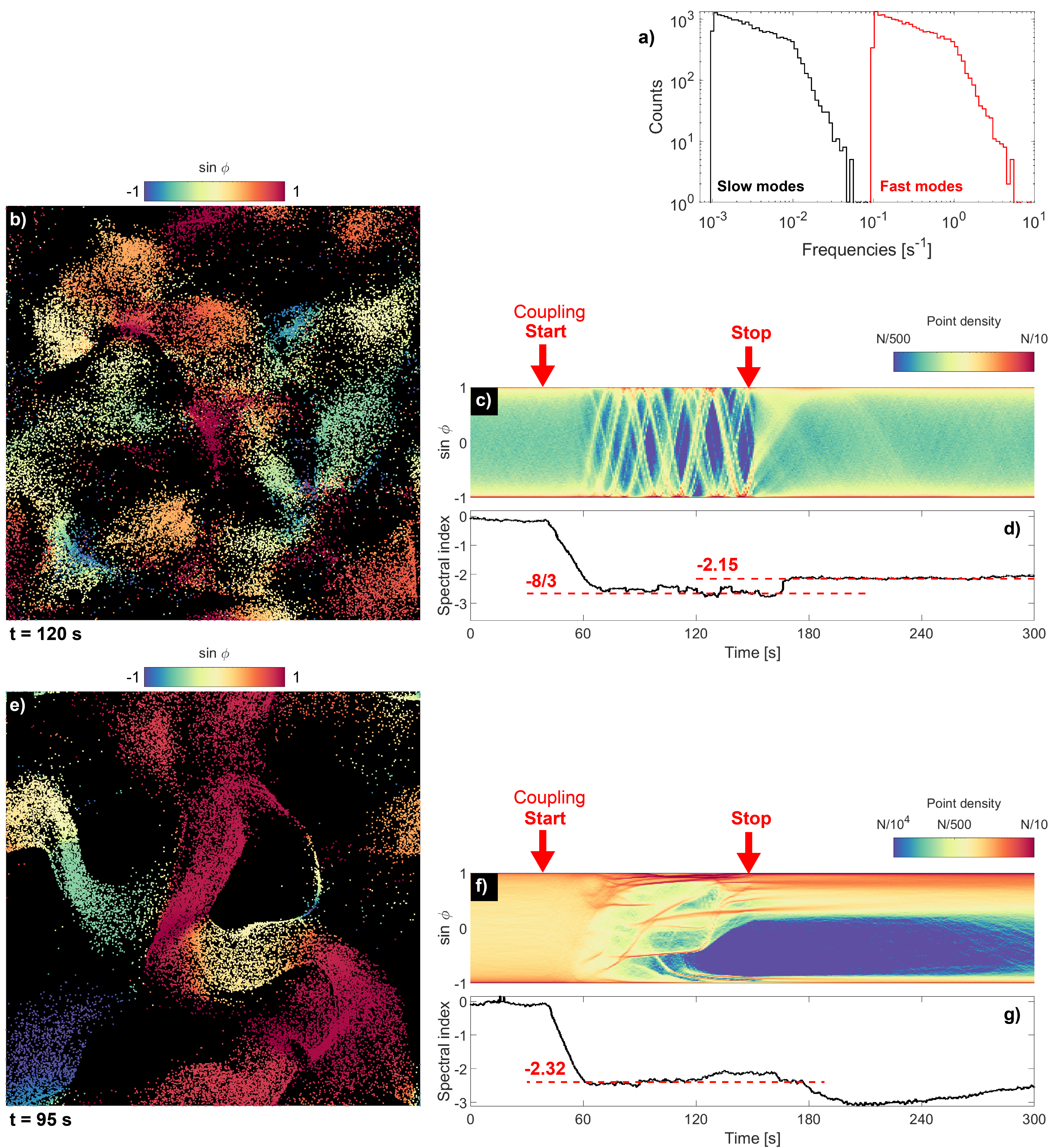
Figure 2: Distributions of natural frequencies, spatial organization snapshots, time-phase-density diagrams, and timeseries of measured spectral slopes for fast and slow modes.

The spectral index steepens with the breaking of initial chaotic symmetry and stabilizes during external driving at values between -2.32 and -2.67, depending on the mode. Fast modes yield shallower spectra post-driving, while slow modes maintain steeper indices. Superposed epoch analyses across Monte Carlo ensembles confirm the robustness of these trends, with median spectral indices stabilizing around -2.5 during coupling and relaxing to -2 in the absence of coupling.

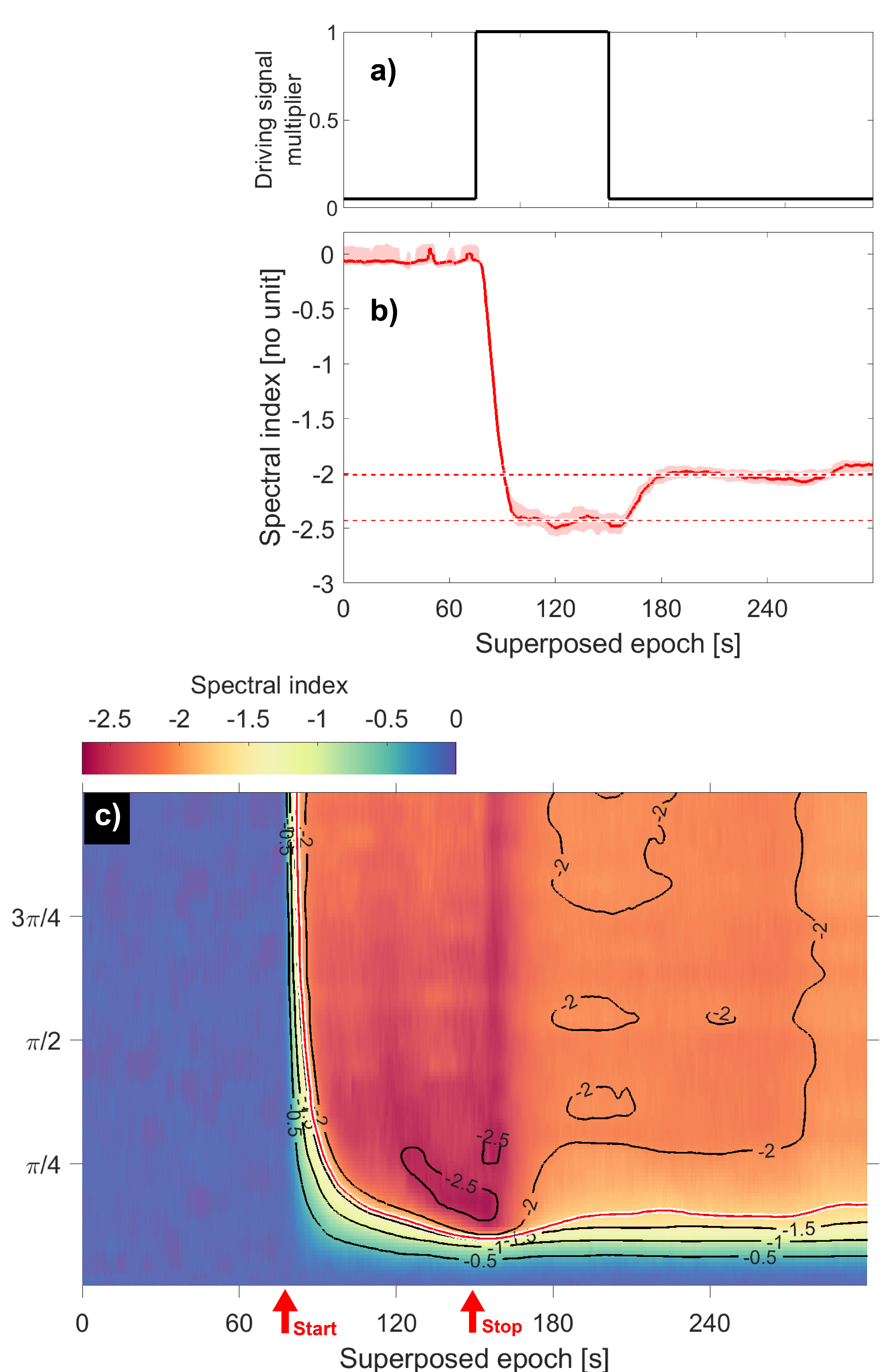
Figure 3: End-state snapshots and superposed epoch analyses of spectral index across Monte Carlo iterations, demonstrating stability and universality of emergent spectral indices.

Further Monte Carlo analyses with persistent external driving show that the spectral index quickly stabilizes, exhibiting weak dependence on coupling strength and moderate dependence on the mode spectrum. Fast modes consistently produce steeper spectra than slow modes.

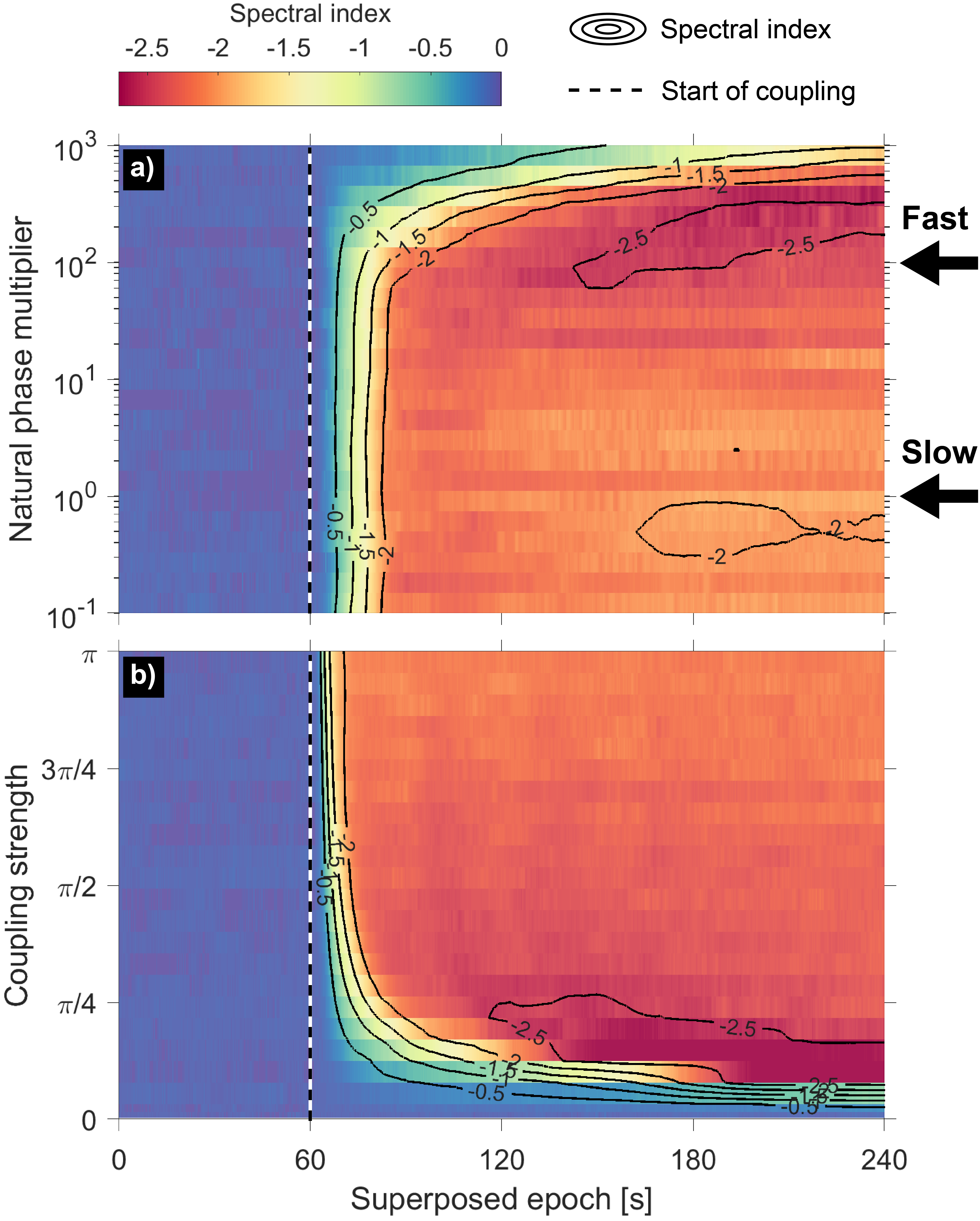
Figure 4: Monte Carlo estimation of average spectral indices as functions of natural phase multiplier and base coupling strength, showing rapid stabilization and universality.

Discussion and Implications

The principal finding is the apparent universality of steep, dissipative spectral indices ($\alpha \approx -2$ to $-3$) in self-organized, phase-synchronized oscillator ensembles. These values are consistent with those observed in plasma turbulence, particularly in kinetic-scale magnetohydrodynamic turbulence, where indices near -8/3 are prevalent. The results suggest that macroscopic structuring in many-body systems may arise from self-organization driven by dimensionality and interaction topology, rather than specific physical processes.

The synthetic nature of the simulations, while not directly modeling real plasma systems, provides a versatile framework for exploring the statistical mechanics of emergence. The findings support the hypothesis that universal scaling laws in spectral density can be reproduced by generic self-organized systems, independent of the governing equations of motion (e.g., Vlasov or MHD).

The velocity alignment mechanism underlying phase synchronization is fundamental to a wide range of systems, including biological collectives and space plasmas. The demonstrated ability to reproduce turbulent spectral characteristics through oscillator-based self-organization has direct implications for understanding the origin of structure in the auroral ionosphere and other plasma environments.

Conclusion

This paper provides compelling evidence that universal spectral density scaling laws can emerge from self-organized structuring in locally coupled oscillator ensembles. The observed spectral indices are robust, steep, and consistent with those found in turbulent plasma systems, suggesting that self-organization may play a fundamental role in the macroscopic structuring of complex systems. Future work should extend these simulations to incorporate more realistic physical interactions and explore the applicability of these principles to specific astrophysical and geophysical contexts.