There must be an error here! Experimental evidence on coding errors' biases (2508.20069v1)

Abstract: Quantitative research relies heavily on coding, and coding errors are relatively common even in published research. In this paper, we examine whether individuals are more or less likely to check their code depending on the results they obtain. We test this hypothesis in a randomized experiment embedded in the recruitment process for research positions at a large international economic organization. In a coding task designed to assess candidates' programming abilities, we randomize whether participants obtain an expected or unexpected result if they commit a simple coding error. We find that individuals are 20% more likely to detect coding errors when they lead to unexpected results. This asymmetry in error detection depending on the results they generate suggests that coding errors may lead to biased findings in scientific research.

• The paper demonstrates that candidates are 20% more likely to detect coding errors when outputs defy prior expectations, exposing inherent bias in error recognition.
• It employs a randomized experiment with manipulated coding tasks among research candidates to classify error detection behaviors systematically.
• The study highlights that mandatory code reviews and transparency reforms can mitigate systematic bias, reinforcing the need for robust research practices.

Experimental Evidence on Coding Errors' Biases in Quantitative Research

Introduction and Motivation

This paper investigates a critical behavioral mechanism underlying the reproducibility crisis in empirical research: the conditional probability of detecting coding errors as a function of whether the resulting output aligns with prior expectations. The authors embed a randomized experiment within the recruitment process for research positions at the World Bank, leveraging a coding task to systematically manipulate whether a simple coding error produces expected or unexpected results. The central hypothesis is that individuals are more likely to debug and detect errors when the output is surprising, potentially introducing systematic bias into published findings.

Experimental Design and Identification Strategy

The experiment utilizes a data task inspired by RCTs in education, where missing values in the outcome variable are coded as 99—a common real-world scenario. Candidates are randomized into two groups: in one, failing to handle missing values yields an unexpected negative effect in the first regression (Q3), while in the other, it yields an expected positive effect. The design enables identification of four latent types of error detection behavior: Always-spot (AS), Never-spot (NS), Complier I (CI, spot only when result is unexpected), and Complier II (CII, spot only when results are conflicting).

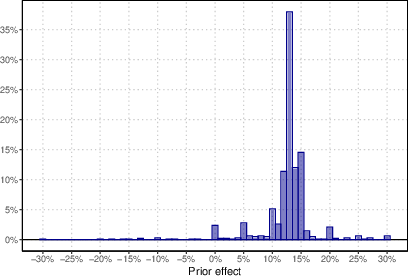
Figure 1: Histogram of prior effect, showing the distribution of candidates' prior beliefs about the expected treatment effect.

The identification strategy exploits the random assignment of dataset versions and the sequential structure of the task. By comparing the proportion of candidates who spot the error in Q3 between treatment and control, the authors estimate the prevalence of CI types. A complementary approach uses Q4 to identify those who spot the error only after observing conflicting results, further refining the estimate.

Sample Characteristics and Task Structure

The sample comprises 1,065 candidates across two recruitment waves, with 805 qualifying as proficient in OLS regression. Demographic and skill variables (gender, education, econometrics coursework, programming language) are balanced across treatment arms, ensuring internal validity.

Figure 2: Demographic breakdown of task takers, including gender and education level.

Figure 3: Distribution of computational languages used by candidates (Stata, R, Python, Other).

The task sequence includes: (1) demographic survey, (2) literature review anchoring priors, (3) elicitation of prior beliefs, (4) data analysis questions (Q1–Q4), and (5) opportunity to revise answers. The critical manipulation occurs in Q3 and Q4, where the coding error's impact is randomized.

Figure 4: Literature review interface, presenting prior RCT results to anchor candidate expectations.

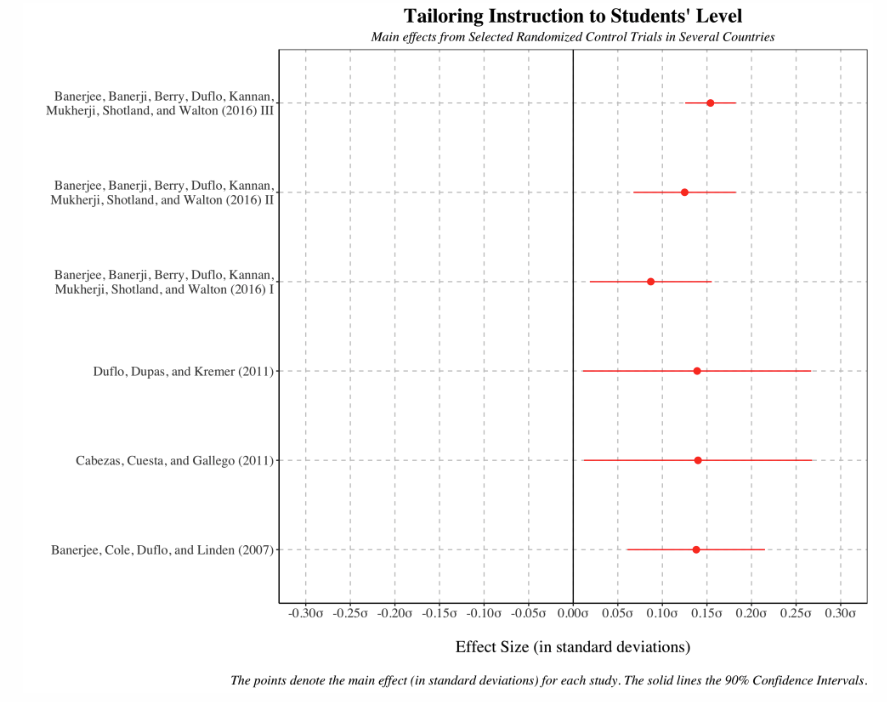
Figure 5: Literature review continuation, reinforcing the expectation of positive treatment effects.

Figure 6: Example scenario and instructions for the hypothetical RCT data analysis.

Figure 7: Elicitation of prior beliefs about the expected treatment effect.

Figure 8: Data interface for the coding task, including the data dictionary highlighting the 99 code for missing values.

Empirical Results

The main finding is that candidates are 20% more likely to detect coding errors when those errors produce unexpected results. In the qualified sample, the baseline probability of spotting the error is 7.6%, increasing by 1.38 percentage points (pp) when the error yields an unexpected outcome. This effect is robust across alternative samples and estimation strategies (OLS, combined estimator, GMM), with p-values consistently below conventional significance thresholds.

Figure 9: Interface for Question 1, assessing basic data manipulation skills.

Figure 10: Interface for Question 2, assessing OLS regression proficiency.

Figure 11: Interface for Question 3, where the coding error's impact is randomized.

Figure 12: Interface for Question 4, mirroring Q3 with the alternate dataset.

Heterogeneity analysis reveals that the effect is present across gender, programming language, and coding proficiency. Notably, more skilled candidates (higher initial scores, correct clustering of standard errors) have higher baseline detection rates but are not less susceptible to the bias; in fact, point estimates of the treatment effect are larger in these subgroups.

Theoretical and Practical Implications

The results demonstrate that error detection is not a neutral process but is conditional on the alignment of results with prior beliefs. This introduces a behavioral channel for systematic bias in empirical research, even absent intentional misconduct. The findings have direct implications for the interpretation of placebo tests and robustness checks, where expected or favorable results may be less scrutinized, increasing the risk of undetected errors.

Figure 13: Interface for revising answers, allowing candidates to correct earlier mistakes before final submission.

Institutional practices such as mandatory code disclosure, pre-publication code review, and increased transparency can mitigate this bias by altering researchers' incentives and increasing anticipated scrutiny. The evidence supports the expansion of such policies to reduce both excess dispersion and systematic bias in published estimates.

Conclusion

This paper provides experimental evidence that the probability of detecting coding errors is significantly higher when those errors yield unexpected results. The implication is that coding errors can introduce not only excess variance but also bias into empirical findings, challenging the assumption that such errors are random noise. The results reinforce the necessity of institutional reforms to promote transparency and rigorous error detection in quantitative research. Future work should explore the generalizability of these findings across disciplines and error types, as well as the effectiveness of different policy interventions in reducing bias from undetected coding errors.