SLIM: Subtrajectory-Level Elimination for More Effective Reasoning (2508.19502v1)

Abstract: In recent months, substantial progress has been made in complex reasoning of LLMs, particularly through the application of test-time scaling. Notable examples include o1/o3/o4 series and DeepSeek-R1. When responding to a query, these models generate an extended reasoning trajectory, during which the model explores, reflects, backtracks, and self-verifies before arriving at a conclusion. However, fine-tuning models with such reasoning trajectories may not always be optimal. Our findings indicate that not all components within these reasoning trajectories contribute positively to the reasoning process; in fact, some components may affect the overall performance negatively. In this study, we divide a reasoning trajectory into individual subtrajectories and develop a "5+2" framework to: (1) systematically identify suboptimal subtrajectories within the reasoning trajectory based on five human-established criteria; (2) assess the independence of the suboptimal subtrajectories identified in (1) from the subsequent content, ensuring that their elimination does not compromise overall flow and coherence of the reasoning process. Additionally, a sampling algorithm, built upon the "5+2" framework, is employed to select data whose reasoning process is free from suboptimal subtrajectories to the highest degree. Experimental results demonstrate that our method can reduce the number of suboptimal subtrajectories by 25.9\% during the inference. Furthermore, our method achieves an average accuracy of 58.92\% on highly challenging math benchmarks with only two thirds of training data, surpassing the average accuracy of 58.06\% achieved with the entire data, and outperforming open-source datasets, when fine-tuning Qwen2.5-Math-7B. Finally, We validated our method under resource constraints and observed improved performance across various inference token limits.

• The paper introduces SLIM, a framework that systematically removes inefficient subtrajectories in multi-step reasoning to improve model accuracy.
• It employs a novel '5+2' evaluation and token-weighted aggregation to balance reasoning quality with diversity.
• Empirical results demonstrate a ~26% reduction in suboptimal reasoning steps and higher accuracy with reduced training data.

Subtrajectory-Level Elimination for More Effective Reasoning in LLMs

Introduction

The paper introduces SLIM, a data curation and sampling framework designed to enhance the reasoning efficacy of LLMs by systematically identifying and eliminating suboptimal subtrajectories within multi-step reasoning outputs. The motivation stems from the observation that RL-finetuned LLMs, while capable of generating extended and exploratory reasoning trajectories, often include inefficient or counterproductive reasoning steps. These suboptimal subtrajectories, if used for supervised fine-tuning (SFT), can degrade both model accuracy and the quality of generated reasoning. SLIM addresses this by introducing a "5+2" framework for subtrajectory assessment and elimination, coupled with a sampling algorithm that balances data quality and diversity in reasoning structure.

The "5+2" Framework: Subtrajectory Assessment and Elimination

SLIM decomposes each reasoning trajectory into subtrajectories, each representing a distinct approach or step in the problem-solving process. The framework applies five human-defined criteria to each subtrajectory:

1. Effort: The subtrajectory must not only propose a method but also attempt its application in context.
2. Effectiveness: The approach should advance the solution, simplify the problem, or clarify limitations.
3. Coherence: Logical continuity must be maintained, with no unjustified leaps.
4. Preliminary Conclusion: Each subtrajectory should reach an intermediate or final conclusion before transitioning.
5. Valid Verification: Redundant or repeated verifications are penalized.

Subtrajectories failing any criterion are flagged as suboptimal. However, elimination is contingent on independence: if a suboptimal subtrajectory introduces variables or results used later, it is retained to preserve logical flow. Otherwise, it is excised.

This two-stage process—identification and independence assessment—constitutes the "5+2" framework. The result is a refined reasoning trajectory with minimized inefficiency and preserved coherence.

Quality Scoring and Token-Weighted Aggregation

Each subtrajectory is scored on the five criteria, and these scores are aggregated into a quality score for the entire reasoning process. Crucially, SLIM introduces token-count-based weighting: longer subtrajectories contribute more to the overall score, and longer suboptimal subtrajectories incur greater penalties. This approach is empirically shown to outperform equal-weighted aggregation.

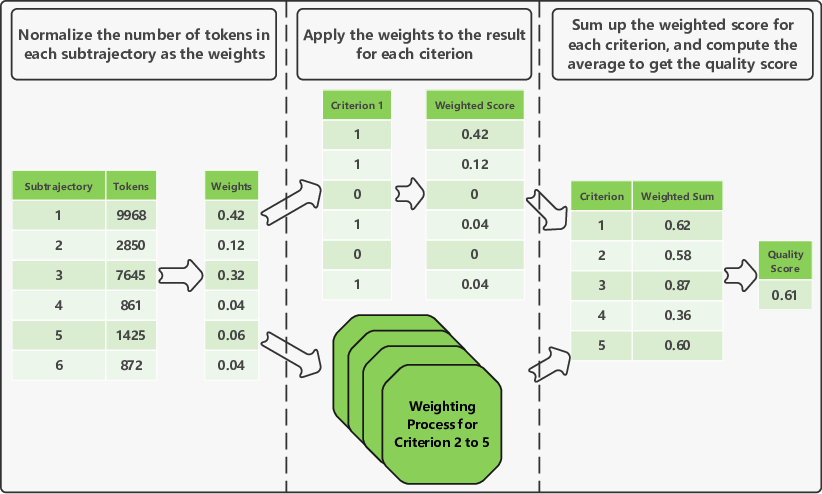
Figure 1: Demonstration of varied weights based on token counts, emphasizing the impact of longer subtrajectories on overall quality.

Sampling Algorithm: Balancing Quality and Reasoning Diversity

After scoring, SLIM samples QA pairs for SFT based on both quality and the distribution of subtrajectory counts. The sampling algorithm penalizes deviations in the number of subtrajectories between the sampled and full datasets using KL divergence, ensuring that the SFT data does not overrepresent shallow or deep reasoning patterns. This prevents the model from overfitting to either overly concise or excessively verbose reasoning styles, maintaining the model's exploratory capacity.

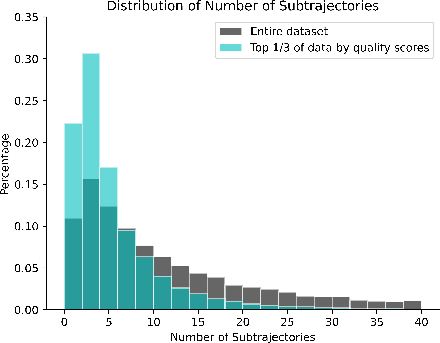
Figure 2: Number of subtrajectories within QA pairs selected by quality scores, illustrating the shift toward fewer subtrajectories after quality filtering.

Experimental Results and Ablation Studies

Main Results

SLIM is evaluated by fine-tuning Qwen2.5-Math-7B on curated datasets (OpenSourceR1-Hard and DeepMath-Hard) and benchmarking on AIME24, AIME25, AMC24, and MATH500. The framework achieves an average accuracy of 58.92% on these challenging benchmarks using only two-thirds of the training data, surpassing the 58.06% accuracy obtained with the full dataset. Notably, SLIM outperforms all compared open-source datasets, including much larger ones, when controlling for model and training configuration.

Suboptimal Subtrajectory Reduction

SLIM reduces the number of suboptimal subtrajectories during inference by 25.9% (OpenSourceR1-Hard) and 26.4% (DeepMath-Hard), indicating a substantial improvement in the quality and efficiency of generated reasoning.

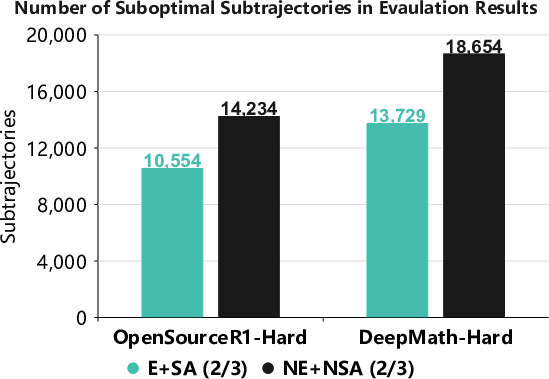
Figure 3: Average number of suboptimal subtrajectories, demonstrating a significant reduction after applying SLIM.

Thinking Efficacy and Underthinking Mitigation

SLIM increases the average number of tokens per subtrajectory while reducing the total number of subtrajectories, indicating deeper, more focused reasoning and less frequent switching between approaches. This directly addresses the "underthinking" phenomenon, where models prematurely abandon reasoning paths.

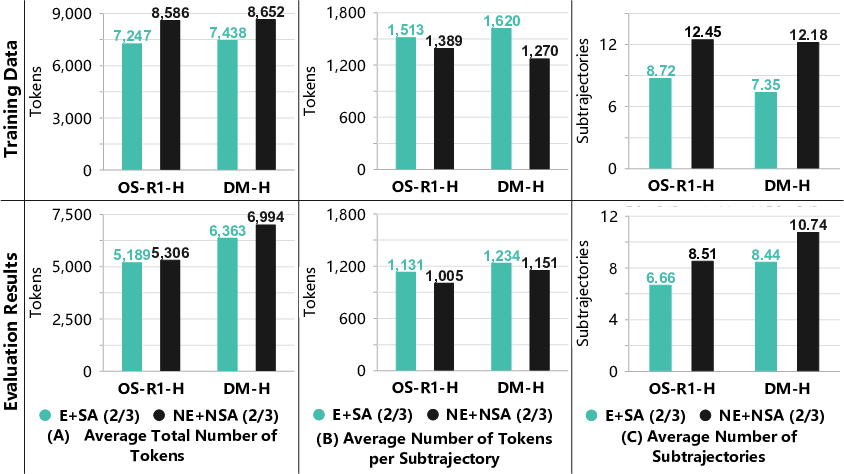
Figure 4: Comparison of metrics for thinking efficacy between training data and evaluation results, showing reduced total tokens, increased tokens per subtrajectory, and fewer subtrajectories after SLIM.

Robustness to Thinking Budget

SLIM maintains superior accuracy across a range of inference token budgets (2k–16k), demonstrating robustness to resource constraints.

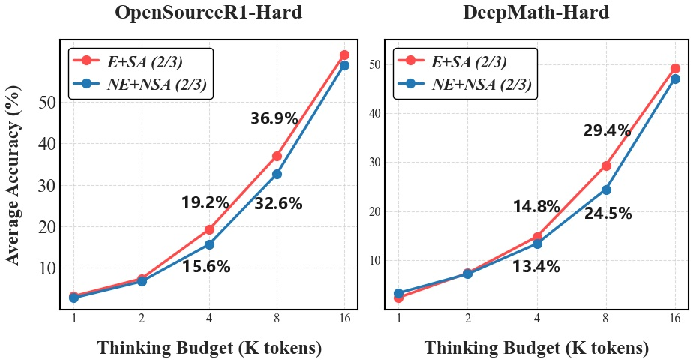
Figure 5: Accuracy of E+SA and NE+NSA with respect to the thinking budget, showing consistent gains for SLIM across budgets.

Ablation Studies

• Token-weighted vs. Equal-weighted Scoring: Token-weighted aggregation yields higher accuracy (58.92% vs. 56.74% on OpenSourceR1-Hard).
• Sampling Algorithm Impact: Incorporating the sampling algorithm further improves performance (58.92% with vs. 58.60% without on OpenSourceR1-Hard).

Implementation Considerations

Data Pipeline

• Subtrajectory Segmentation: Requires robust parsing of model outputs to delineate subtrajectories, typically using cue phrases ("Alternatively", "Another method", etc.).
• Automated Evaluation: Prompts a strong LLM (e.g., QwQ-32B) to assess each subtrajectory against the five criteria and independence.
• Tokenization: Accurate token counting is essential for weighted aggregation.
• Sampling: KL divergence computation and iterative sampling are used to match subtrajectory count distributions.

Resource Requirements

• Training: Full-parameter SFT on Qwen2.5-Math-7B, consuming 576 Ascend 910B4 NPU hours per run.
• Inference: Evaluation uses pass@1 under zero-shot CoT, with up to 16k output tokens.

Limitations

• Domain Specificity: The framework is tailored to domains with multi-step reasoning and may require adaptation for fields with different reasoning paradigms.
• Diversity vs. Quality: Aggressive quality filtering may reduce data diversity, potentially impacting generalization.

Practical and Theoretical Implications

SLIM demonstrates that fine-grained, subtrajectory-level data curation can yield measurable improvements in both accuracy and reasoning quality for LLMs, even with reduced data volume. The approach is particularly effective in mathematical domains where reasoning trajectories are long and complex. Theoretically, SLIM provides a principled method for aligning SFT data with desired reasoning behaviors, mitigating both overthinking and underthinking phenomena.

Future Directions

• Domain Generalization: Extending the "5+2" framework to other domains (e.g., physics, code generation) will require domain-specific criteria and segmentation strategies.
• Scaling to Larger Models: Applying SLIM to models with >32B parameters may yield further gains, especially as model capacity increases.
• Automated Subtrajectory Assessment: Improving the automation and reliability of subtrajectory evaluation, possibly via dedicated reward models or self-supervised signals.

Conclusion

SLIM provides a systematic, scalable approach to improving LLM reasoning by eliminating suboptimal subtrajectories and balancing data quality with reasoning diversity. The empirical results substantiate the claim that careful curation at the subtrajectory level can yield both higher accuracy and more effective, efficient reasoning, setting a new standard for SFT data preparation in complex reasoning domains.