Bit Threads: From Entanglement to Geometric Entropies (2508.18941v1)
Abstract: In this work, we attempt to construct bit threads configurations for various backgrounds using expressions from CPS formalism. We find that when the Ryu-Takayanagi surface is same as horizon, such expressions are sufficient. In other cases, it differs by gradient of a harmonic function. We explore its relation to Wald and differential entropy, and re-express the first law of entanglement entropy in terms of bit threads. Inclusion of quantum effects imposes some constraints on the bulk entanglement via the dominant energy condition. We also apply our method to ascertain bit thread configuration in certain dynamical spacetime.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Bit Threads: From Entanglement to Geometric Entropies — A Simple Guide
Overview
This paper studies a new way to picture and calculate how parts of a quantum system are connected, using something called bit threads. Think of bit threads like thin strings that represent how much two regions are “entangled” (quantumly linked). The authors show how to build these threads using a general, symmetry-based method from physics called the covariant phase space (CPS) formalism. They also connect this picture to other types of entropy (a measure of “information content”), like black hole entropy and differential entropy, and discuss what changes when quantum effects are included or when spacetime is changing with time.
What questions does the paper ask?
- Can we construct bit threads in a systematic, symmetry-driven way (using CPS), instead of guessing them case by case?
- When does this CPS method work “out of the box,” and when do we need to tweak the threads?
- Can the same flow-of-threads idea explain black hole entropy and differential entropy?
- How do “first laws” (small changes in entropy) look in the bit-thread language?
- What limits do quantum effects place on these flows?
How did the researchers approach the problem?
To make the paper’s ideas more familiar, here’s a simple picture for each main step:
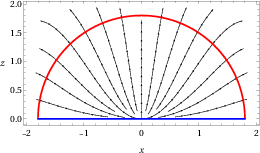
- Bit threads as flows: Imagine a landscape where water flows from one side to another. The total amount of water that can squeeze through the narrowest pass (the “bottleneck”) tells you how strongly the two sides are connected. In holography (a theory linking gravity and quantum systems), that bottleneck is a special surface in the bulk called the Ryu–Takayanagi (RT) surface, and the total “flow” equals the entanglement entropy.
- Using CPS (symmetries → conserved flows): CPS is a toolkit that turns spacetime symmetries (like time shifts or rotations) into conserved quantities. In the water analogy, a symmetry gives you a particular way the water can flow without piling up or draining away—this is called “divergence-free,” meaning no sources or sinks. The authors turn CPS “currents” into vector fields (flows) that can serve as candidate bit threads.
- The fine-tuning step (a gentle nudge): A valid bit-thread flow must follow two rules: it must be divergence-free (no sources or sinks) and must obey a “speed limit” (a maximum strength everywhere), plus it must “saturate” on the bottleneck (align with the RT surface at the bound). CPS naturally gives divergence-free flows, but they don’t always hit the exact bound at the RT surface. The fix: add the gradient of a “harmonic function” (think of a smooth, gentle height map) to nudge the flow, without changing its overall counting. This is a harmless adjustment that keeps the flow divergence-free.
- Testing in examples:
- In Poincaré AdS3 (a standard curved spacetime used in holography), the raw CPS flow is not enough; the authors add the “gentle nudge” (harmonic adjustment) so the flow hits the RT surface perfectly.
- In Rindler AdS3 (a wedge-shaped view adapted to an accelerating observer), the RT surface matches a horizon (an edge of no return), and the CPS flow already works with no adjustment needed.
- They also show you can transform a working flow in Rindler coordinates into a good flow in Poincaré coordinates using coordinate changes alone—no extra guessing required.
- Extending beyond entanglement:
- Black hole (Wald) entropy: Using the same CPS-based flows, the “flux” through the black hole’s horizon equals the black hole’s entropy.
- Differential entropy: For spacetimes with holes, summing up many overlapping boundary regions leads to a “differential entropy,” which the authors also express as a flux of the right CPS-derived flow.
- First laws and quantum effects:
- First laws: Small changes in entropy (for entanglement, black holes, and differential entropy) can all be written as small changes in the corresponding flows—giving a unified, geometric language.
- Quantum corrections: Including quantum effects adds limits based on energy conditions (like the “dominant energy condition,” which, roughly speaking, says energy doesn’t move faster than light). These conditions restrict how much extra “quantum” entanglement the threads can represent.
What did they find, and why does it matter?
- A symmetry-based construction of threads: CPS naturally produces divergence-free flows (good candidates for bit threads). This gives a principled way to build thread configurations instead of relying on special tricks or heavy calculations.
- When the RT surface is a horizon, no extra fix is needed: In Rindler-AdS (and similar settings where the RT surface equals a horizon), the CPS flow already satisfies all the thread rules. This makes those cases especially clean.
- In other cases, add a harmonic “nudge”: When the RT surface is not a horizon (like in Poincaré AdS), you can add a gradient of a harmonic function to make the CPS flow satisfy the bit thread bounds and match the RT surface exactly. This adjustment doesn’t change the overall counting (it’s like re-routing without changing how much water passes through).
- Coordinate transformations can carry flows across frames: A correct flow in one coordinate system (Rindler) can be turned into a correct flow in another (Poincaré) by changing coordinates, avoiding the need to find the RT surface by hand.
- Unifying different entropies: The same flow idea captures black hole entropy (Wald entropy) and differential entropy as fluxes, creating one geometric picture for several types of entropy.
- First laws become flow statements: Small changes in entropy follow from small changes in the CPS-derived flows, offering a simple, unified language for thermodynamics-like relations in gravity.
- Quantum limits from energy conditions: When you include quantum effects, energy conditions in the bulk limit how large the “quantum” part of the entropy can be. That means the geometry and energy content of spacetime put real constraints on entanglement.
These results matter because they strengthen the bridge between geometry (curved spacetime) and quantum information (entanglement). They also provide new tools to paper time-dependent situations like thermalization or black hole evaporation, where tracking entanglement is especially important.
What’s the impact and where could this go?
- A general recipe: The CPS-based method offers a recipe for constructing bit threads that’s tied to symmetries, not guesswork. This could make it easier to paper complicated spacetimes.
- One language for many entropies: Writing entanglement entropy, black hole entropy, and differential entropy as fluxes of related flows suggests these different ideas are really faces of the same underlying structure.
- Better tools for dynamics: Extending these threads to fully time-dependent (covariant) cases could help us understand real processes—how systems thermalize, how information escapes or gets scrambled near black holes, and how quantum geometry evolves.
- Quantum gravity insights: Because the method ties together symmetry, geometry, and information, it might help us uncover deeper rules of quantum gravity, including limits set by energy conditions and quantum corrections.
In short, the paper shows how to build and use “flows of entanglement” in a clean, symmetry-driven way, connects them to key entropy concepts in gravity, and sets the stage for studying more realistic, time-dependent, and quantum-corrected spacetimes.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, focused list of gaps and unresolved questions that emerge from the paper. Each item is framed to enable concrete follow-up by future researchers.
- Precise criteria for when CPS-derived flows are sufficient: Identify geometric and symmetry conditions under which the CPS flow
v_cps^aautomatically satisfies the bit-thread norm bound and RT-surface saturation without requiring the additional divergence-free termv_d^a(e.g., classification beyond cases where RT surface coincides with a horizon). - Systematic construction of the correction term: Develop a general, algorithmic method to construct the harmonic function
φ(with∇^2 φ = 0) that yieldsv_d^a = ∇^a φ, including uniqueness, boundary conditions, and regularity; extend to higher dimensions and arbitrary boundary regions. - Non-simply connected manifolds and cohomology: Provide a practical prescription for choosing the co-exact, divergence-free correction
v_d^awhen the domain is not simply connected (wherev_d^acannot be written as a gradient), including a classification by de Rham cohomology classes and constraints from topology and homology. - Robustness against CPS ambiguities and boundary terms: Quantify the impact of CPS residual ambiguities (e.g.,
Θ → Θ − dB) and CPSB boundary contributions (C,ℓ) on the resulting bit-thread field and flux; propose a gauge-fixing or canonical choice that ensures uniqueness and physical interpretability of the flow. - General validity beyond exact symmetries: The construction relies on exact symmetries (Killing vectors). Develop methods to construct canonical bit threads in spacetimes with approximate or no exact symmetries (e.g., generic, inhomogeneous, or chaotic geometries).
- Extension to time-dependent (covariant) settings: Provide explicit constructions of covariant CPS-based bit threads in dynamical spacetimes, demonstrate consistency with HRT extremal surfaces, and address causality, existence/uniqueness, and flux maximization in Lorentzian signature.
- Proof of norm bound saturation: Give general, non-perturbative conditions or proofs showing that CPS flows (with or without
v_d^a) saturate the norm bound on the extremal/minimal surface and thus realize max-flow/min-cut in diverse geometries. - Higher-dimensional and generic boundary regions: Extend explicit constructions (currently shown for AdS3 and intervals) to higher-dimensional AdS and arbitrary-shaped boundary subregions, including practical algorithms for computing
v_d^aand enforcing boundary anchoring. - Factor normalization and dimensional consistency: Clarify and systematize the appearance of dimensionful factors (e.g., the
1/(4 G_N L)prefactor obtained after coordinate transformations), and ensure consistency between flux normalization and entropy units across coordinate frames. - Relation to geodesic-based flows: Establish a general correspondence (or conditions for equivalence) between CPS-derived flows and geodesic-constructed symmetric flows; explain when coordinate transformations from Rindler-AdS to Poincaré intrinsically reproduce geodesic flows.
- Black hole entropy flows beyond simple cases: Complete explicit CPS-based thread constructions for rotating BTZ and higher-dimensional black holes, including extremal/near-extremal cases (where bifurcation surfaces may be absent) and non-AdS asymptotics.
- Wald entropy in higher-curvature gravity: Demonstrate that CPS-derived bit threads reproduce the appropriate generalized entropy (Dong–Camps–Wald prescriptions) in higher-curvature/modified gravity theories; provide explicit examples and discuss corrections to the norm bound.
- Differential entropy via CPS flows: Construct explicit CPS-derived flows that compute differential entropy in spacetimes with holes (both holographic and non-holographic), and clarify uniqueness, boundary anchoring, and conditions ensuring that the flux equals differential entropy.
- First-law formulations beyond linear variations: Extend CPS/bit-thread-based first-law derivations beyond linear order and parametric variations, include matter fields explicitly, and verify for higher-curvature theories and mixed states.
- Integration of quantum effects: Provide a concrete scheme for including bulk entanglement in CPS-derived flows (quantum extremal surfaces, FLM/Engelhardt–Wall corrections), and replace/augment DEC constraints with appropriate quantum energy conditions (e.g., QNEC, averaged null energy) to ensure validity.
- Physical meaning and fixing of gauge freedom: Clarify the physical interpretation of the “gauge” component
v_d^a(e.g., longitudinal thread rearrangements that preserve total flux) and propose principles (symmetry, minimal norm, regularity) to fix this freedom uniquely. - Numerical and algorithmic implementations: Develop PDE-based or optimization algorithms (e.g., method of characteristics, convex optimization) to compute CPS flows and the corrective
φin complex geometries without closed-form solutions; provide benchmarks and error analysis. - Multi-region and multipartite entanglement: Explore whether CPS-based canonical threads can systematically capture mutual information, monogamy constraints, entanglement of purification, and multipartite entanglement measures, and specify how to construct flows for multiple regions simultaneously.
- Matter couplings and non-gravitational fields: Generalize the CPS-based construction to include gauge fields and other matter contributions within the codim-2 current, and determine how these affect the bit-thread constraints and resulting entropic fluxes.
- Mapping to arbitrary CFT regions via isometries: Formalize the use of bulk isometries (beyond simple boosts) to map canonical flows between coordinate systems and boundary regions; characterize limits of this approach when such isometries or foliation structures are absent.
- Regularity and boundary behavior: Prove existence, regularity, and boundary behavior of
φand the composed flow near the boundary (z → 0) and around extremal surfaces; specify admissible singularities and ensure numerical stability. - Entanglement wedge and minimal cuts: Provide a general method to ensure that CPS-derived flows respect entanglement wedge boundaries and homologous minimal cuts, including criteria for identifying the correct bottleneck surface without prior knowledge.
- Empirical validation and benchmarks: Supply numerical tests comparing CPS-based thread fluxes to RT/HRT areas across diverse spacetimes (including perturbed and random geometries), quantify deviations, and assess sensitivity to CPS ambiguities and boundary conditions.
Practical Applications
Immediate Applications
These applications can be implemented now using the methods, examples, and workflows developed in the paper.
- Canonical bit-thread construction for static AdS backgrounds
- Sector: academia, software
- Use case: Compute holographic entanglement entropy (HEE) without explicitly determining RT surfaces in cases where the RT surface coincides with a horizon (e.g., AdS-Rindler), and in Poincaré AdS via coordinate transformations.
- Potential tool/workflow: “Canonical Bit-Thread Solver” that takes a metric and a Killing vector, computes the CPS codimension-2 current
j_ξ, maps it via Hodge dual to a divergenceless vector fieldv_cps, and adds a harmonic correction∇φto satisfy norm and saturation constraints; supports Rindler-to-Poincaré mapping to produce flows equivalent to geodesic constructions. - Assumptions/dependencies: Exact symmetries (Killing vectors), simply connected domains (to express co-exact correction as
∇φ), valid AdS/CFT setting, reliable PDE solver for Laplace’s equation. Tools:xAct/Mathematica, SageManifolds, SymPy, FEniCS.
- Entropy-by-flow for Wald and differential entropy in symmetric spacetimes
- Sector: academia, software
- Use case: Compute Wald entropy of black hole horizons and differential entropy of spacetimes with “holes” as fluxes of CPS-derived flows; cross-check known results and unify entropy notions via a flow paradigm.
- Potential tool/workflow: “Flow Entropy Calculator” with modules for horizon flux (Wald entropy) and hole geometries (differential entropy) using
j_ξassociated with relevant Killing vectors; integrates with symbolic geometry engines and mesh-based integrators. - Assumptions/dependencies: Stationary spacetimes with well-defined bifurcation surfaces, validity of the Iyer–Wald formalism, appropriate boundary conditions at horizons and asymptotic boundaries.
- Coordinate-transformation workflow to bypass RT surface identification
- Sector: academia, software
- Use case: Generate valid bit threads in Poincaré AdS by transforming flows constructed in AdS-Rindler (where RT coincides with the horizon), reproducing symmetric flows without prior geodesic/RT search.
- Potential tool/workflow: “Flow Transformer” that applies analytic coordinate maps (including boosts) from AdS-Rindler to Poincaré patches, outputting
vfields that saturate bounds on target RT surfaces. - Assumptions/dependencies: Availability of analytic coordinate maps, numerical stability of transformed fields, adherence to flow constraints in new coordinates.
- First-law checks via CPS flows
- Sector: academia
- Use case: Re-express and verify the first law of entanglement entropy, black hole entropy, and differential entropy as variations of CPS-derived fluxes; perform consistency checks for small deformations.
- Potential tool/workflow: “First-Law Validator” that computes
δH_ξvia∫∂Σ k_ξand compares to flux variations across relevant codimension-2 surfaces; integrates with perturbative solvers. - Assumptions/dependencies: Linearized variations within CPS, availability of symplectic potentials and
k_ξexpressions, clean boundary terms.
- Interactive visualization for education and outreach
- Sector: education, daily life (STEM outreach)
- Use case: Visualize bit-thread lines, entanglement regions, and horizons to teach entanglement geometry, HEE, and black hole entropy.
- Potential tool/workflow: Web-based visual engine (e.g., Python + Plotly/WebGL) that renders flows from
v(z,x)and highlights RT surfaces and saturation; includes sliders for interval size and boosts. - Assumptions/dependencies: Precomputed or runtime flow fields; accuracy of geometry-to-visualization mapping.
- Entropy inequality testing in toy holographic models
- Sector: academia
- Use case: Use CPS-based flows to test monogamy of mutual information and related inequalities under controlled deformations.
- Potential tool/workflow: “Inequality Tester” that takes boundary partitions, constructs candidate flows, and numerically verifies inequality saturation/violation scenarios.
- Assumptions/dependencies: Validity of the bit-thread max-flow/min-cut duality in the model regime; control over boundary partitions and bulk geometry.
- PDE-based boundary condition enforcement for flows
- Sector: academia, software
- Use case: Systematize the addition of harmonic corrections
∇φto CPS flows to satisfy the unit-norm bound and saturation at RT/horizon surfaces. - Potential tool/workflow: “Harmonic Corrector” solving
∇²φ=0with boundary conditions derived from RT/horizon normals, feeding corrections back intov=v_cps+∇φ. - Assumptions/dependencies: Well-posedness of Laplace problems on chosen slices, adequate meshing near boundaries/horizons.
Long-Term Applications
These applications will require further research, scaling, or development, especially to generalize beyond static, highly symmetric cases and to incorporate quantum and dynamical effects.
- Covariant bit threads for dynamical spacetimes (thermalization, quenches, evaporation)
- Sector: academia, software
- Use case: Model time-dependent entanglement dynamics (HRT setting) using families of CPS-consistent flows; paper thermalization profiles, quench dynamics, and aspects of black hole evaporation.
- Potential tool/product: “Covariant Thread Simulator” supporting foliations, dynamical HRT surfaces, and time-dependent
k_ξ/j_ξconstruction. - Assumptions/dependencies: Robust covariant generalization of CPS flows to non-static settings, numerical stability in evolving geometries, integration with Hubeny–Rangamani–Takayanagi extremal surfaces.
- Quantum-corrected bit threads and energy-condition informed bounds
- Sector: academia, quantum information
- Use case: Incorporate bulk quantum effects into flows via constraints from the dominant energy condition (DEC) and related semiclassical inputs to bound bulk entanglement and generalized entropy.
- Potential tool/product: “Quantum Flow Constraint Checker” that applies energy-condition bounds to candidate flows, informing viable semiclassical states and holographic code constructions.
- Assumptions/dependencies: Precise formulation of quantum bit threads, validity of DEC or its quantum refinements, availability of quantum stress-energy inputs.
- Generalized entropy in higher-curvature gravities via canonical flows
- Sector: academia, software
- Use case: Extend canonical flow construction to higher-curvature theories (e.g., Gauss–Bonnet, Lovelock) to compute generalized entropies (Wald-like) and entanglement measures.
- Potential tool/product: “Higher-Curvature Entropy Suite” with CPS modules adapted to modified Lagrangians and boundary terms.
- Assumptions/dependencies: Availability of consistent
k_ξ/j_ξin modified theories, resolution of ambiguity in symplectic potentials and boundary conditions.
- Entanglement routing and capacity planning in quantum networks (flow-inspired heuristics)
- Sector: telecommunications, quantum computing
- Use case: Adapt capacity-limited flow intuitions (max-flow/min-cut) from bit threads to design entanglement distribution and routing policies across quantum repeaters and network topologies.
- Potential tool/product: “Entanglement Routing Optimizer” that models entanglement resources as threads with capacity constraints and optimizes multi-party distribution.
- Assumptions/dependencies: Mapping from geometric flow heuristics to discrete quantum network graphs, integration with practical constraints (noise, fidelity, decoherence), empirical validation.
- Automated discovery of extremal surfaces via global flow saturation
- Sector: academia, software
- Use case: Find RT/HRT surfaces by globally optimizing flows to saturate norm bounds; replace geodesic search with variational flow methods.
- Potential tool/product: “Extremal Surface Finder” using flow saturation principles and PDE-constrained optimization.
- Assumptions/dependencies: Convergence of global optimization in complex geometries, accurate handling of cohomology classes and gauge freedoms in
j_ξ.
- Machine learning surrogates for entanglement via flow fields
- Sector: software, academia
- Use case: Train ML models on CPS-derived flow datasets to predict entanglement entropy, differential entropy, or horizon entropy across families of geometries.
- Potential tool/product: “FlowNet-HEE” delivering fast surrogate predictions for geometry-to-entropy mappings.
- Assumptions/dependencies: Availability of labeled datasets (geometry, flow, entropy), generalization beyond training geometries, interpretability for physics use.
- Cross-checking semiclassical gravity proposals and code-based holography
- Sector: academia
- Use case: Use CPS-thread first-law formulations to test consistency of new semiclassical gravity models, including holographic codes and bulk reconstruction protocols.
- Potential tool/product: “Semiclassical Consistency Suite” incorporating first-law and flux-based checks against code-based constructions.
- Assumptions/dependencies: Mature integration of CPS with holographic codes, controlled approximations for bulk reconstruction, careful treatment of quantum corrections.
Collections
Sign up for free to add this paper to one or more collections.