Attention Layers Add Into Low-Dimensional Residual Subspaces (2508.16929v1)

Abstract: While transformer models are widely believed to operate in high-dimensional hidden spaces, we show that attention outputs are confined to a surprisingly low-dimensional subspace, where about 60\% of the directions account for 99\% of the variance--a phenomenon that is induced by the attention output projection matrix and consistently observed across diverse model families and datasets. Critically, we find this low-rank structure as a fundamental cause of the prevalent dead feature problem in sparse dictionary learning, where it creates a mismatch between randomly initialized features and the intrinsic geometry of the activation space. Building on this insight, we propose a subspace-constrained training method for sparse autoencoders (SAEs), initializing feature directions into the active subspace of activations. Our approach reduces dead features from 87\% to below 1\% in Attention Output SAEs with 1M features, and can further extend to other sparse dictionary learning methods. Our findings provide both new insights into the geometry of attention and practical tools for improving sparse dictionary learning in LLMs.

• The paper reveals that attention outputs in Transformer models are confined to a low-dimensional subspace primarily induced by the output projection matrix.
• By using singular value decomposition, the study quantifies how a reduced number of principal components efficiently recovers most of the downstream loss.
• Active Subspace Initialization is introduced to align SAE features with the active subspace, dramatically reducing dead features and improving reconstruction error.

Attention Output Layers Operate in Low-Dimensional Residual Subspaces

Introduction and Motivation

The paper "Attention Layers Add Into Low-Dimensional Residual Subspaces" (2508.16929) provides a comprehensive empirical and theoretical analysis of the geometric structure of attention outputs in Transformer models. Contrary to the common assumption that attention mechanisms operate in high-dimensional spaces, the authors demonstrate that the outputs of attention layers are confined to surprisingly low-dimensional subspaces. This low-rank structure is shown to be a universal property across model families, layers, and datasets, and is primarily induced by the anisotropy of the output projection matrix $W^O$.

The work further establishes a direct link between this low-rank structure and the prevalence of dead features in sparse dictionary learning methods, such as sparse autoencoders (SAEs). The authors propose Active Subspace Initialization (ASI), a principled initialization scheme that aligns SAE features with the active subspace of activations, dramatically reducing dead features and improving reconstruction quality. The implications of these findings are significant for both mechanistic interpretability and the efficient scaling of sparse dictionary learning in LLMs.

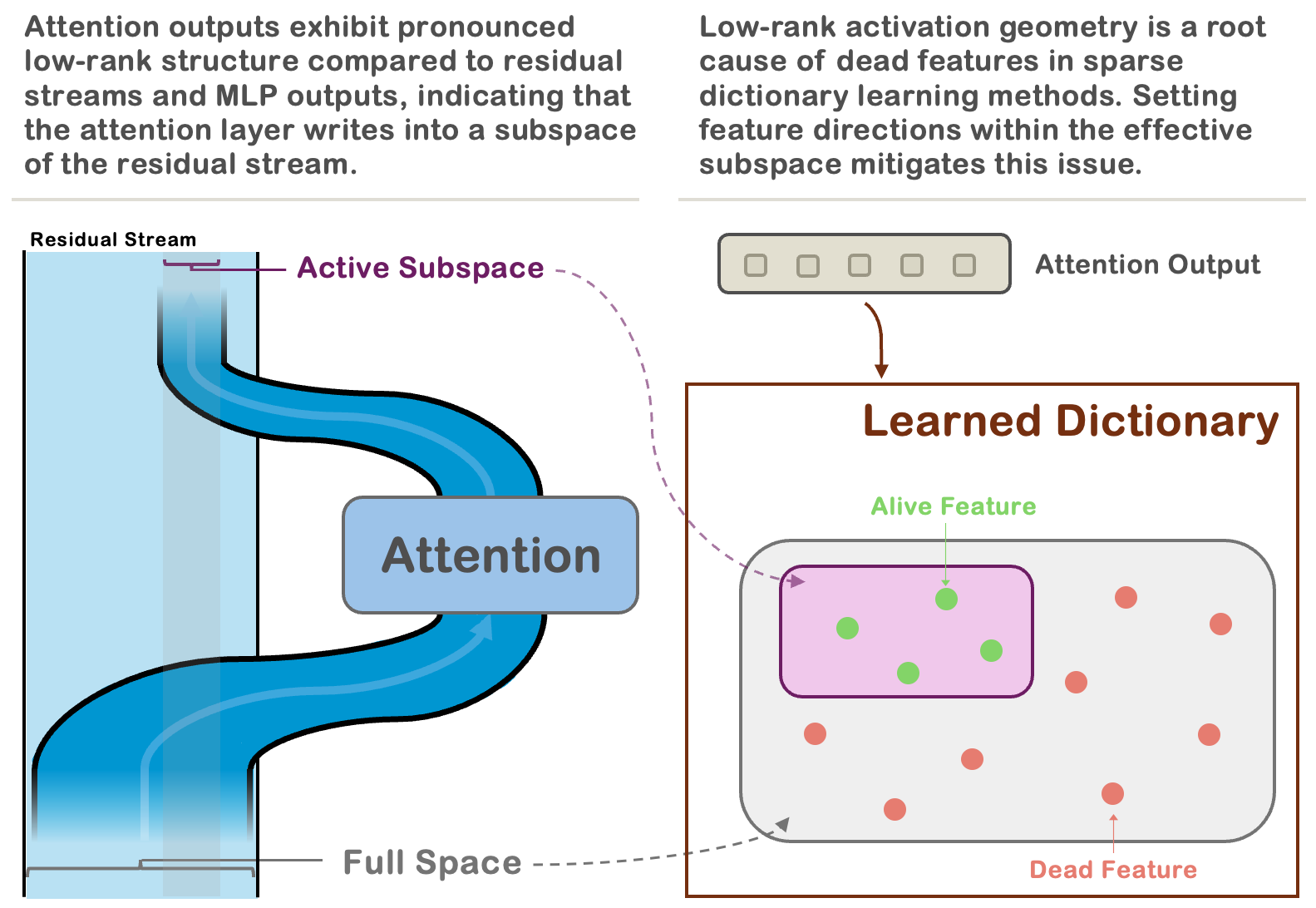
Figure 1: Schematic illustration of the low-rank structure in attention outputs and their relationship to the residual stream.

Empirical Characterization of Low-Rank Attention Outputs

Intrinsic Dimension and Spectral Decay

The central empirical finding is that attention outputs exhibit a much lower intrinsic dimension than both MLP outputs and the residual stream. Quantitatively, approximately 60% of the principal directions account for 99% of the variance in attention outputs, whereas MLP and residual activations require over 90% of directions to reach the same threshold. This is robustly observed across layers, model families (e.g., Llama-3.1-8B, Qwen3-8B, Gemma-2-9B), and datasets (SlimPajama, RedPajamaGithub, CCI3-Data).

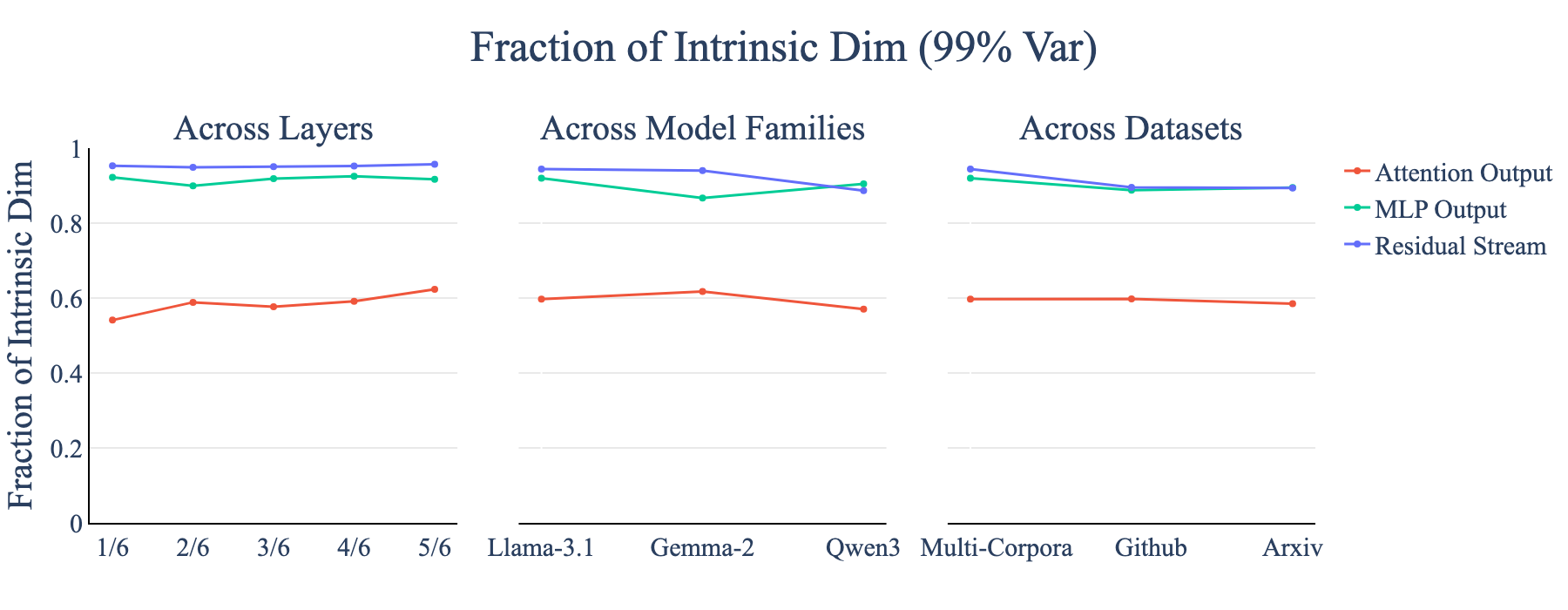
Figure 2: Across layers, model families, and datasets, attention outputs (red) consistently exhibit lower intrinsic dimension than residual streams (blue) and MLP outputs (green).

Singular value decomposition (SVD) of the activation matrices reveals a rapid spectral decay for attention outputs, with a small number of singular values capturing the majority of the variance. This low-rankness is not an artifact of specific data or model choices but a universal property of Transformer attention mechanisms.

Downstream Task Efficiency

The low-dimensionality of attention outputs translates into efficient downstream loss recovery: only 25% of the principal components are needed to recover 95% of the downstream loss, compared to 78% and 86% for MLP and residual outputs, respectively. This demonstrates that the information content of attention outputs is highly concentrated.

Mechanistic Origin: The Role of the Output Projection Matrix

The low-rank structure is traced to the output projection matrix $W^O$. While the concatenated multi-head outputs $Z$ are high-dimensional, $W^O$ projects these into a much lower-dimensional subspace. Decomposition of the variance along principal directions shows that the anisotropy of $W^O$ is the dominant factor in compressing the output space.

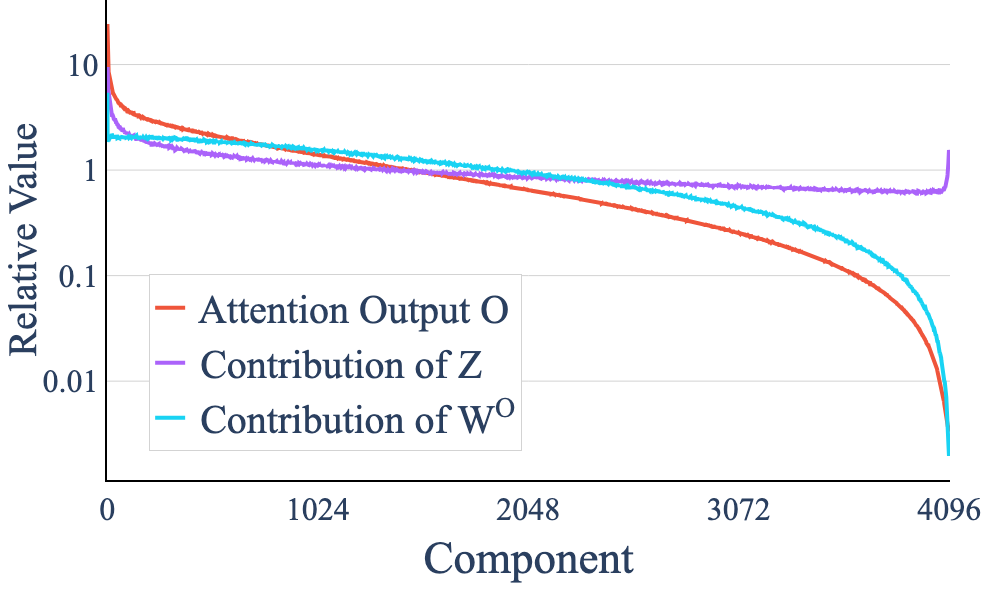
Figure 3: Decomposition of variance in attention output $O$; the low-rank structure is primarily due to the output projection matrix $W^O$.

This finding has implications for both model compression and interpretability, as it suggests that the effective capacity of attention layers is much lower than their parameter count would suggest.

Dead Features in Sparse Dictionary Learning

Empirical Correlation

A strong empirical correlation is established between the intrinsic dimension of activations and the number of dead features in SAEs. Layers with lower intrinsic dimension consistently exhibit a higher proportion of dead features, indicating a mismatch between the randomly initialized SAE weights and the geometry of the activation space.

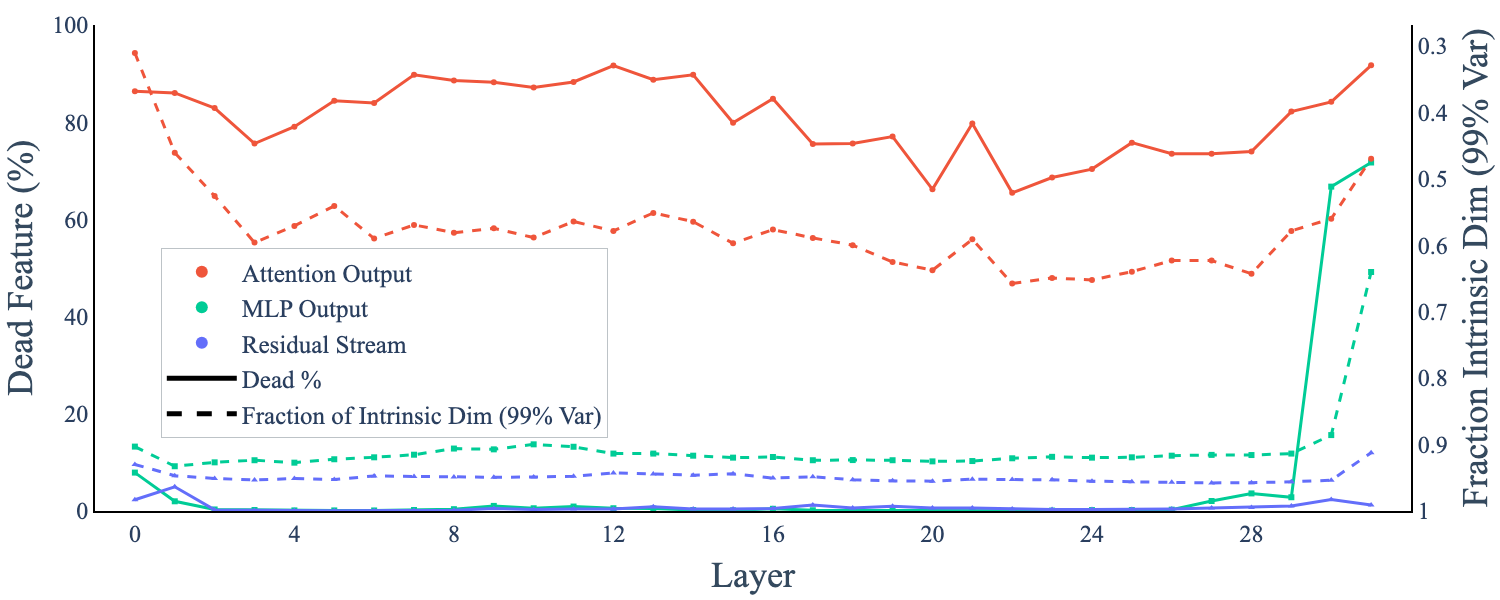
Figure 4: The number of dead features and the intrinsic dimension of each layer in Llama-3.1-8B; lower intrinsic dimension correlates with more dead features.

Active Subspace Initialization

To address this, the authors introduce Active Subspace Initialization (ASI). The method computes the top $d_{\text{init}}$ right singular vectors of the activation matrix and initializes SAE weights within this active subspace. This alignment ensures that SAE features are well-matched to the geometry of the data, dramatically reducing dead features (from 87% to below 1% in large-scale experiments) and improving reconstruction error.

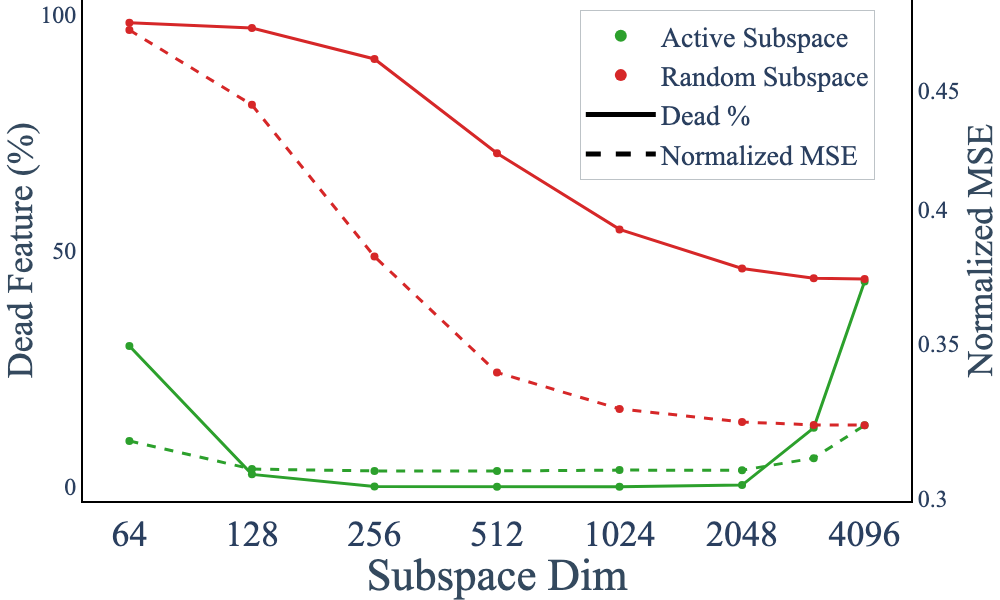
Figure 5: Proportion of dead features and normalized MSE across different subspace dimensions; only initialization with the active subspace yields substantial improvement.

ASI is computationally lightweight, requires no additional loss terms or resampling strategies, and generalizes across architectures and activation types.

Scaling Laws and Optimizer Considerations

Scaling Behavior

ASI demonstrates optimal scaling characteristics: as the number of SAE features increases, reconstruction error decays smoothly, and the number of dead features remains low. At very large scales, some dead features persist, but these do not impact reconstruction quality, indicating that revived features in alternative methods contribute little to actual performance.

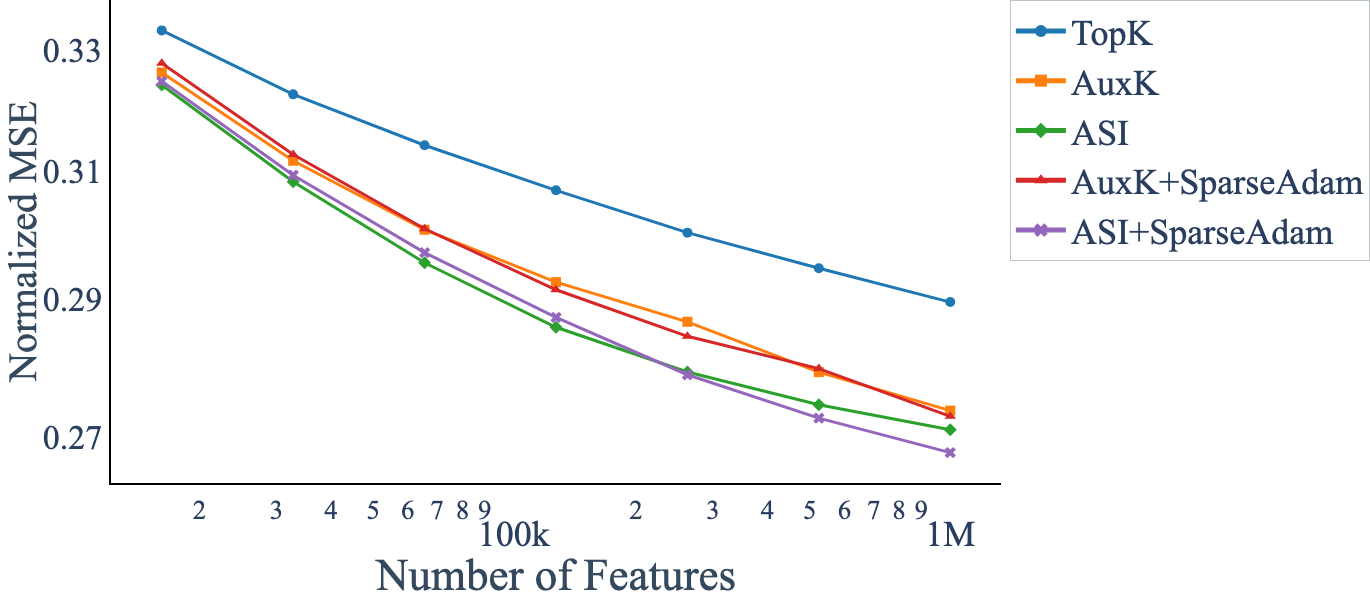
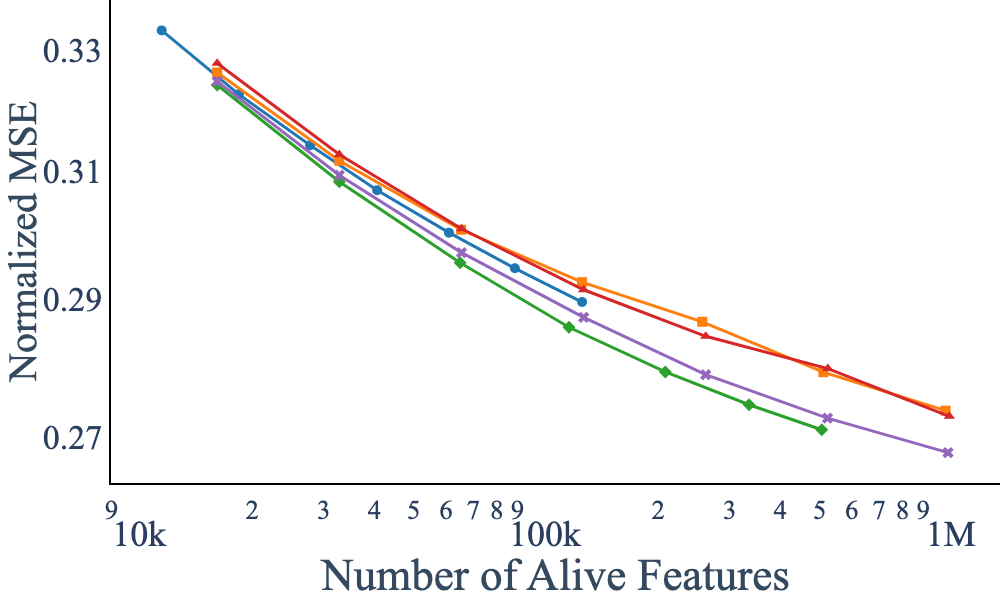
Figure 6: Loss vs. number of parameters; Active Subspace Init consistently achieves lower reconstruction error than baselines.

SparseAdam and Stale Momentum

The paper also identifies stale momentum in optimizers as a secondary cause of dead features. By employing SparseAdam, which updates only active parameters, the formation of dead features is further mitigated, especially at large scales. The combination of ASI and SparseAdam yields the best empirical results.

Generalization to Sparse Replacement Models

The ASI method is shown to generalize to sparse replacement models such as Lorsa, reducing dead parameters and improving reconstruction error. However, complete elimination of dead features in these models may require additional mechanisms, such as tied initialization between encoder and decoder weights.

Implications and Future Directions

Theoretical Implications

The discovery that attention outputs are confined to low-dimensional subspaces challenges prevailing assumptions about the representational capacity of Transformer attention layers. This has implications for the linear representation hypothesis and the design of interpretability tools, suggesting that much of the apparent complexity in attention outputs is illusory.

Practical Implications

For practitioners, the results provide actionable guidance for scaling sparse dictionary learning methods. ASI offers a principled, efficient, and generalizable approach to initializing large SAEs, enabling the extraction of interpretable features at scale without the computational waste associated with dead features. The findings also motivate further exploration of low-rank parameterizations and compression techniques for attention layers.

Future Developments

Future work may investigate the universality of low-rank attention outputs in other modalities and architectures, the interplay between low-rankness and model generalization, and the development of new sparse modeling techniques that explicitly exploit the low-dimensional geometry of attention activations.

Conclusion

This paper establishes that attention outputs in Transformer models are universally low-rank, a property induced by the output projection matrix and consistent across architectures and datasets. This low-rankness is a primary cause of dead features in sparse dictionary learning, which can be effectively addressed by Active Subspace Initialization. The results have significant implications for interpretability, model compression, and the efficient scaling of sparse feature extraction methods in LLMs.