Lorentz-Equivariance without Limitations (2508.14898v2)

Abstract: Lorentz Local Canonicalization (LLoCa) ensures exact Lorentz-equivariance for arbitrary neural networks with minimal computational overhead. For the LHC, it equivariantly predicts local reference frames for each particle and propagates any-order tensorial information between them. We apply it to graph networks and transformers. We showcase its cutting-edge performance on amplitude regression, end-to-end event generation, and jet tagging. For jet tagging, we introduce a large top tagging dataset to benchmark LLoCa versions of a range of established benchmark architectures and highlight the importance of symmetry breaking.

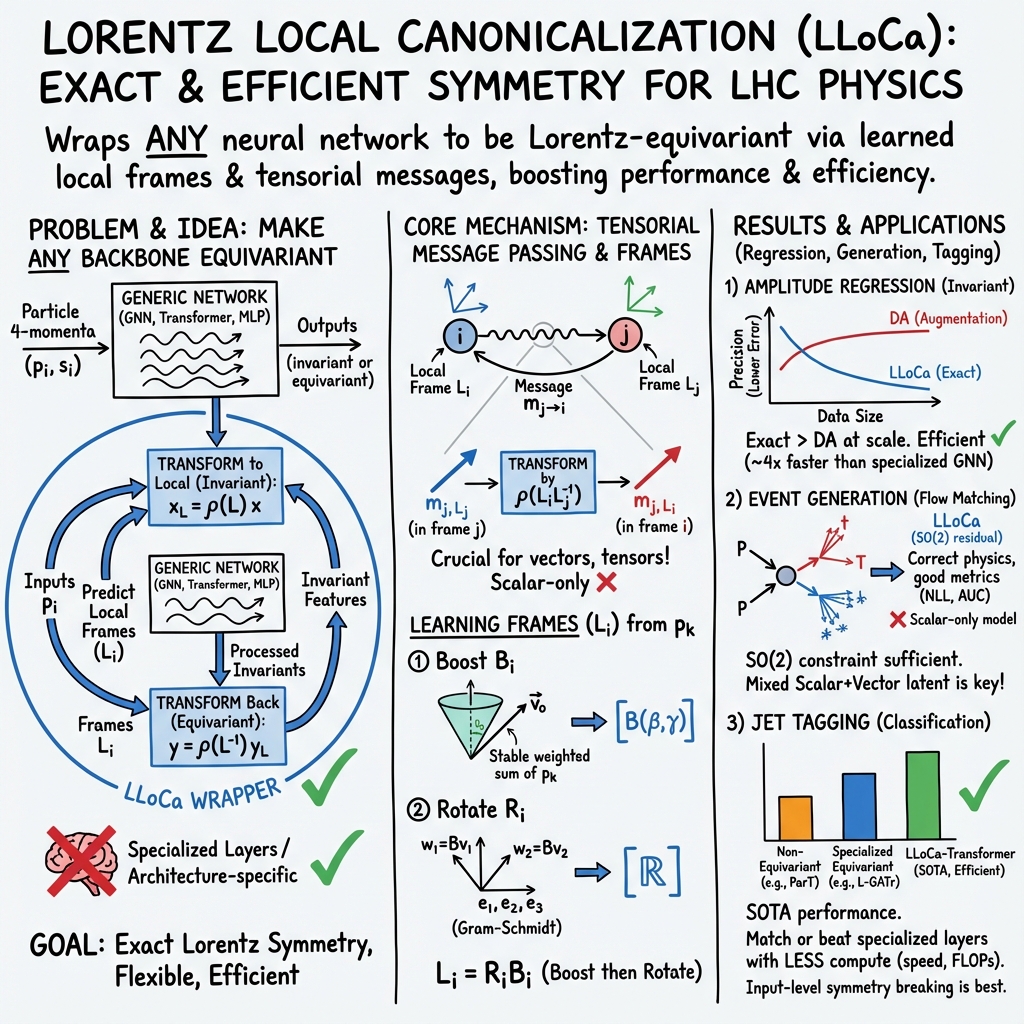
• The paper presents Lorentz Local Canonicalization (LLoCa) as its main contribution, converting various neural network architectures into Lorentz-equivariant models for high-energy physics tasks.
• It demonstrates improved precision in amplitude regression with reduced FLOPs and training times, validated on high-multiplicity events at the LHC.
• The framework also enhances event generation and jet tagging by enabling precise tensorial message passing and adaptable symmetry breaking in models like transformers.

Lorentz-Equivariance without Limitations

Introduction

The paper "Lorentz-Equivariance without Limitations" (2508.14898) introduces an advanced framework for ensuring Lorentz-equivariance in arbitrary neural networks, presenting the Lorentz Local Canonicalization (LLoCa) methodology. This approach is particularly significant for applications at the Large Hadron Collider (LHC), where it enables equivariant predictions of local reference frames for each particle and facilitates tensorial information propagation under Lorentz symmetry. The framework is designed to be computationally efficient and applicable to a wide range of ML architectures, including GNNs and transformers, with minimal overhead, proving its efficacy in amplitude regression, event generation, and jet tagging.

Lorentz Local Canonicalization

The fundamental concept of LLoCa lies in its ability to transform any network architecture into a Lorentz-equivariant version by predicting learnable local reference frames for each particle. These frames are utilized to establish invariance of particle features through tensorial message passing, which is crucial for geometric representation across frames. A pivotal aspect of LLoCa is its independence from specialized layers that are typical in other Lorentz-equivariant architectures, allowing it to maintain the backbone architecture while still achieving exact Lorentz-equivariance. This feature is demonstrated to enhance performance across multiple multiplicity levels and scale efficiently with training data size.

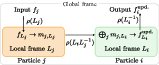
Figure 1: Tensorial message passing in LLoCa. All symbols are described in the text. This figure is also included in Ref.~\cite{Spinner:2025prg.

Amplitude Regression

LLoCa's application in amplitude regression improves the precision of amplitude surrogates, essential for expediting event generation processes in high-energy physics. Benchmarks on processes such as $q\bar{q} \rightarrow Z + ng$ demonstrate the superior precision of LLoCa networks compared to standard architectures like MLP-I and L-GATr. In this context, LLoCa-Transformer outperforms its non-equivariant counterparts, bolstered by fewer FLOPs and decreased training times while retaining a high degree of precision.

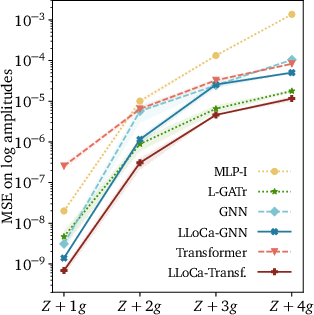
Figure 2: Left: scaling of the prediction error with the multiplicity for all amplitude surrogates. Right: training cost on $Z+4g$ amplitudes.

Event Generation

The paper extends the utility of LLoCa to event generation tasks, where generative networks learn the phase space density efficiently. Utilizing conditional flow matching and embracing the LLoCa-Transformer's capacity for symmetry breaking, event generation is robustly achieved under the influence of $\mathrm{SO}(2)$ symmetry pertinent to LHC detector geometries. The ability to handle high-multiplicity events with accuracy and computational efficiency is highlighted.

Figure 3: Overview of marginal distributions for $t\bar{t}+1,2,3,4$ jets.

Jet Tagging

In jet tagging, LLoCa versions of established architectures like ParticleNet and ParT illustrate the framework's flexibility and scalability. LLoCa taggers achieve state-of-the-art performance on both small and large datasets, adapting symmetry configurations to maximize efficacy. Detailed comparison shows the computational efficiency and improved categorization metrics, with LLoCa-Transformer risings as a prodigious performer amidst rigorous benchmarks.

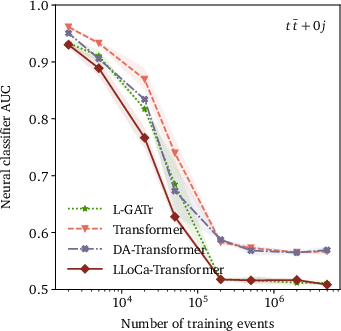
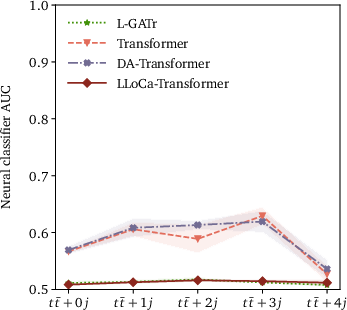
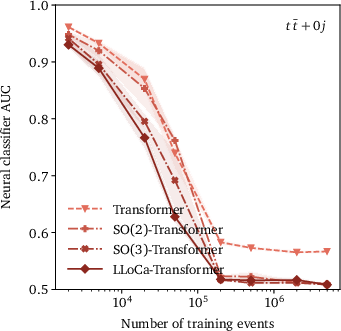
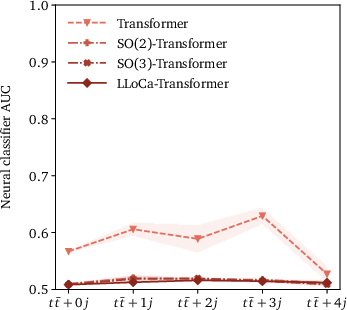
Figure 4: Upper panels: Classifier AUC of the LLoCa-Transformer compared with a non-equivariant transformer, a transformer trained with data augmentation, and L-GATr for event generation. Lower panels: Impact of explicit symmetry breaking on event generation, measured by classifier AUC.

Conclusion

Lorentz Local Canonicalization (LLoCa) showcases a transformative approach for embedding Lorentz invariance in machine learning architectures, catering to challenging tasks in high-energy physics with unprecedented flexibility and performance. LLoCa effectively balances computational efficiency with the demand for symmetry-induced precision, establishing itself as a robust framework capable of revolutionizing scientific inquiries in collider-based particle physics. Its adaptability to symmetry breaking further expands LLoCa’s applicability, paving the way for future explorations in AI-driven physics research.