The C-index Multiverse (2508.14821v1)

Abstract: Quantifying out-of-sample discrimination performance for time-to-event outcomes is a fundamental step for model evaluation and selection in the context of predictive modelling. The concordance index, or C-index, is a widely used metric for this purpose, particularly with the growing development of machine learning methods. Beyond differences between proposed C-index estimators (e.g. Harrell's, Uno's and Antolini's), we demonstrate the existence of a C-index multiverse among available R and python software, where seemingly equal implementations can yield different results. This can undermine reproducibility and complicate fair comparisons across models and studies. Key variation sources include tie handling and adjustment to censoring. Additionally, the absence of a standardised approach to summarise risk from survival distributions, result in another source of variation dependent on input types. We demonstrate the consequences of the C-index multiverse when quantifying predictive performance for several survival models (from Cox proportional hazards to recent deep learning approaches) on publicly available breast cancer data, and semi-synthetic examples. Our work emphasises the need for better reporting to improve transparency and reproducibility. This article aims to be a useful guideline, helping analysts when navigating the multiverse, providing unified documentation and highlighting potential pitfalls of existing software. All code is publicly available at: www.github.com/BBolosSierra/CindexMultiverse.

• The paper reveals that different C-index implementations yield varying model evaluations due to discrepancies in tie handling, censoring adjustments, and risk transformations.
• The analysis combines empirical studies on the METABRIC dataset with simulation experiments to demonstrate sensitivity in model ranking and the bias-variance trade-off of IPCW methods.
• The study underscores the necessity for standardized reporting and transparent methods to ensure reproducible and fair comparisons in survival analysis.

The C-index Multiverse: Discrepancies and Implications in Survival Model Evaluation

Introduction

This paper provides a comprehensive analysis of the concordance index (C-index) as a metric for discrimination in time-to-event (survival) models, focusing on the substantial variability introduced by different software implementations and estimator definitions. The authors systematically dissect the conceptual and practical sources of variation in C-index estimation, including tie handling, censoring adjustment, and risk summarization from survival distributions. The work is motivated by the observation that seemingly equivalent C-index implementations can yield divergent results, undermining reproducibility and complicating fair model comparisons.

Conceptual Framework and C-index Variants

The C-index quantifies a model's ability to correctly rank individuals by risk, given observed time-to-event outcomes. The canonical definition, as proposed by Harrell, is $$C = P(M(\mathbf{x}_i) > M(\mathbf{x}_j) | T_i < T_j)$$, where $M(\cdot)$ is a risk score derived from covariates. However, time-to-event data introduces ambiguity due to censoring and ties in event times or predictions. Several C-index variants have been developed to address these issues:

• Harrell's C-index: Time-independent, based on a risk score; sensitive to censoring and ties.
• Uno's C-index ($C_\tau$): Incorporates time truncation and inverse probability of censoring weights (IPCW) to mitigate bias from censoring.
• Antolini's C-index ($C_{td}$): Directly ranks individuals using the entire survival distribution, bypassing the need for risk score summarization.

The paper highlights that these definitions differ not only in their mathematical formulation but also in their practical implementation, especially regarding the treatment of ties and censoring.

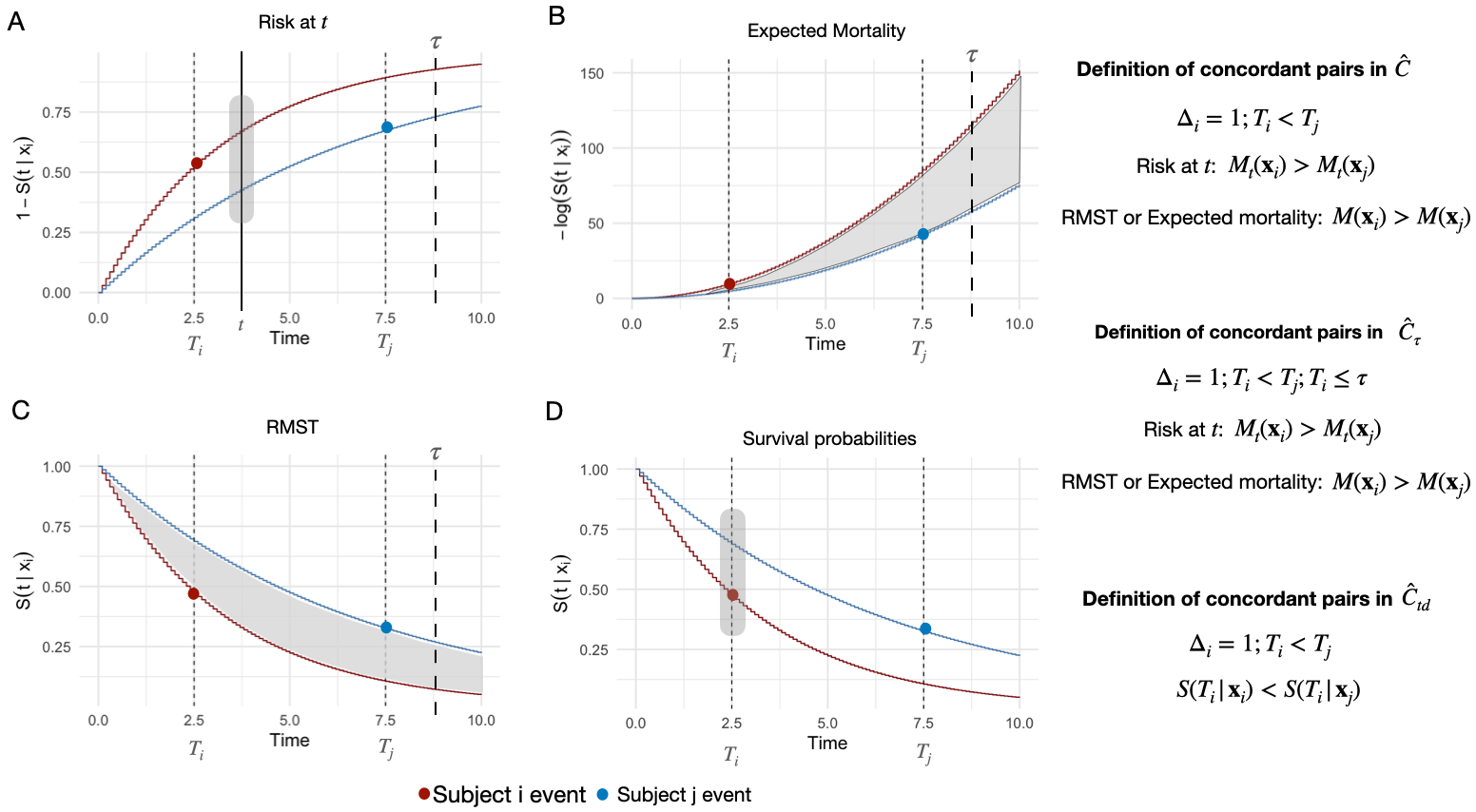
Figure 1: Schematic representation of information used by different C-index estimators when ranking two individuals, illustrating the conceptual differences between $C$, $C_\tau$, and $C_{td}$.

Software Implementation Discrepancies

A central contribution of the paper is the systematic review of C-index implementations in R and Python. The authors demonstrate that even for the same estimator (e.g., Uno's), different packages can produce distinct results due to subtle choices in tie handling, censoring adjustment, and input formatting. For example, some implementations count tied times as comparable only under specific censoring scenarios, while others allow user-defined options for tie inclusion. IPCW calculation methods also vary, with some packages estimating the censoring distribution from the training set and others from the test set, affecting stability and bias.

The lack of standardized documentation and reporting exacerbates these discrepancies, making it difficult for analysts to interpret results or reproduce analyses. The authors provide unified documentation and recommendations for navigating this "C-index multiverse."

Figure 2: Comparison of C-index implementations in the first fold during hold-out cross-validation and bootstrap on the METABRIC dataset, categorized by definition and transformation.

Risk Summarization and Transformation

For estimators requiring a scalar risk score, the transformation of the survival distribution is non-trivial. Common approaches include:

• Time-dependent predictions: $M_t(\mathbf{x}_i) = 1 - S(t|\mathbf{x}_i)$, sensitive to the choice of $t$ and not proper for non-PH models.
• Expected mortality: Aggregates cumulative hazard, but can be numerically unstable for high-risk individuals due to unbounded log terms.
• Restricted Mean Survival Time (RMST): Proposed by the authors as a robust alternative, RMST is always well-defined and interpretable, representing the area under the survival curve up to a clinically relevant time horizon.

The choice of transformation can substantially affect model ranking and discrimination estimates, especially for non-PH and deep learning models.

Empirical Analysis: METABRIC Case Study

Using the METABRIC breast cancer dataset, the authors evaluate several survival models (CPH, RSF, DeepSurv, Cox-Time, DeepHit) across multiple C-index implementations and transformations. Key findings include:

• Model ranking is highly sensitive to the choice of C-index definition and transformation. DeepHit, for example, is ranked highest by $C_{td}$ but lowest by $C$ and $C_\tau$, reflecting its optimization for distributional ranking.
• IPCW adjustment introduces a bias-variance trade-off. While IPCW reduces bias in the presence of censoring, it can inflate variance, especially when time truncation is not properly applied.
• Tie handling has negligible impact in datasets with few ties, but can be significant in others. Sensitivity analyses with artificially increased ties confirm the importance of explicit tie handling options.

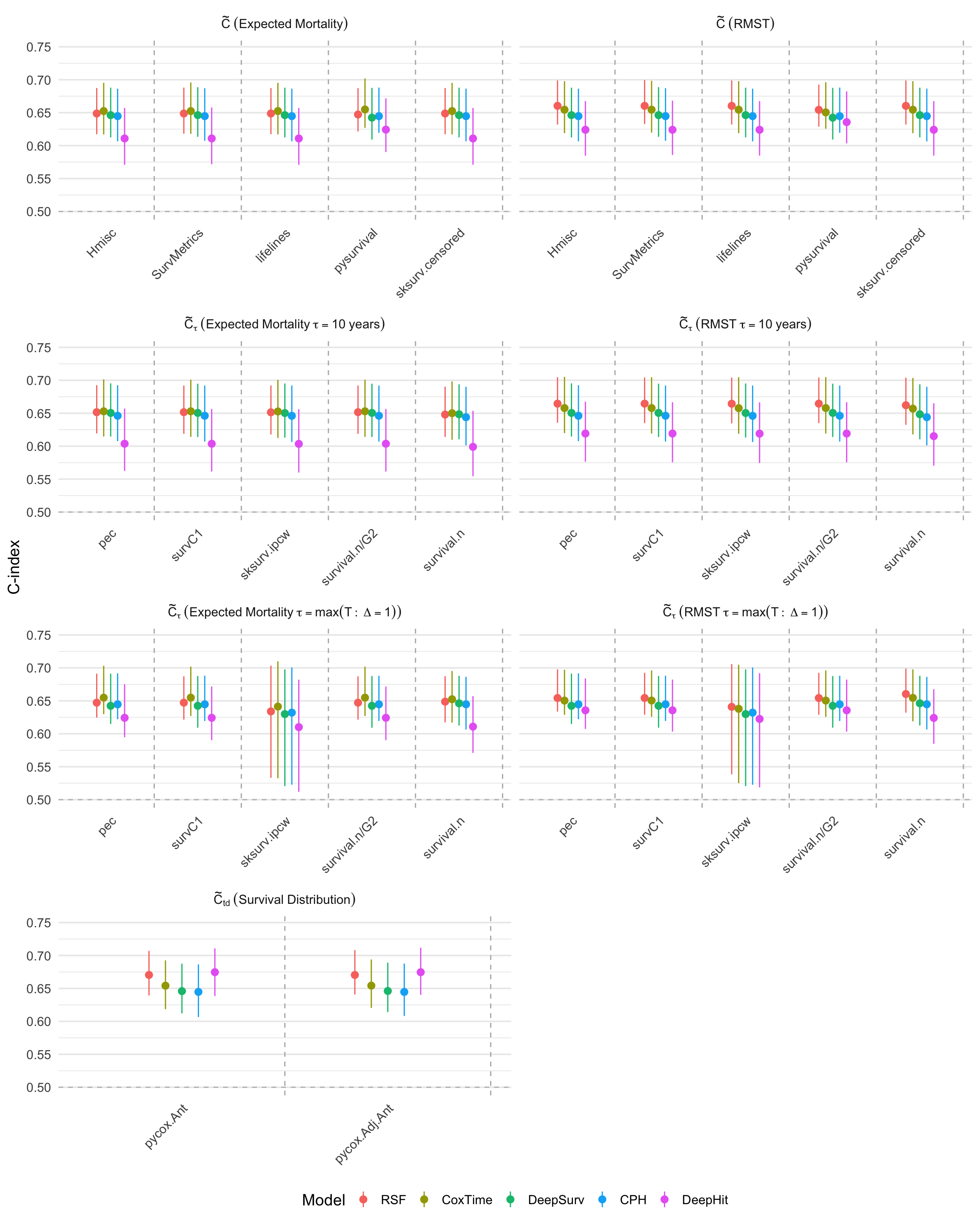
  Figure 3: Comparison of C-index estimates calculated by different implementations on the METABRIC first CV fold, grouped by concordance probability definition and transformation.

  

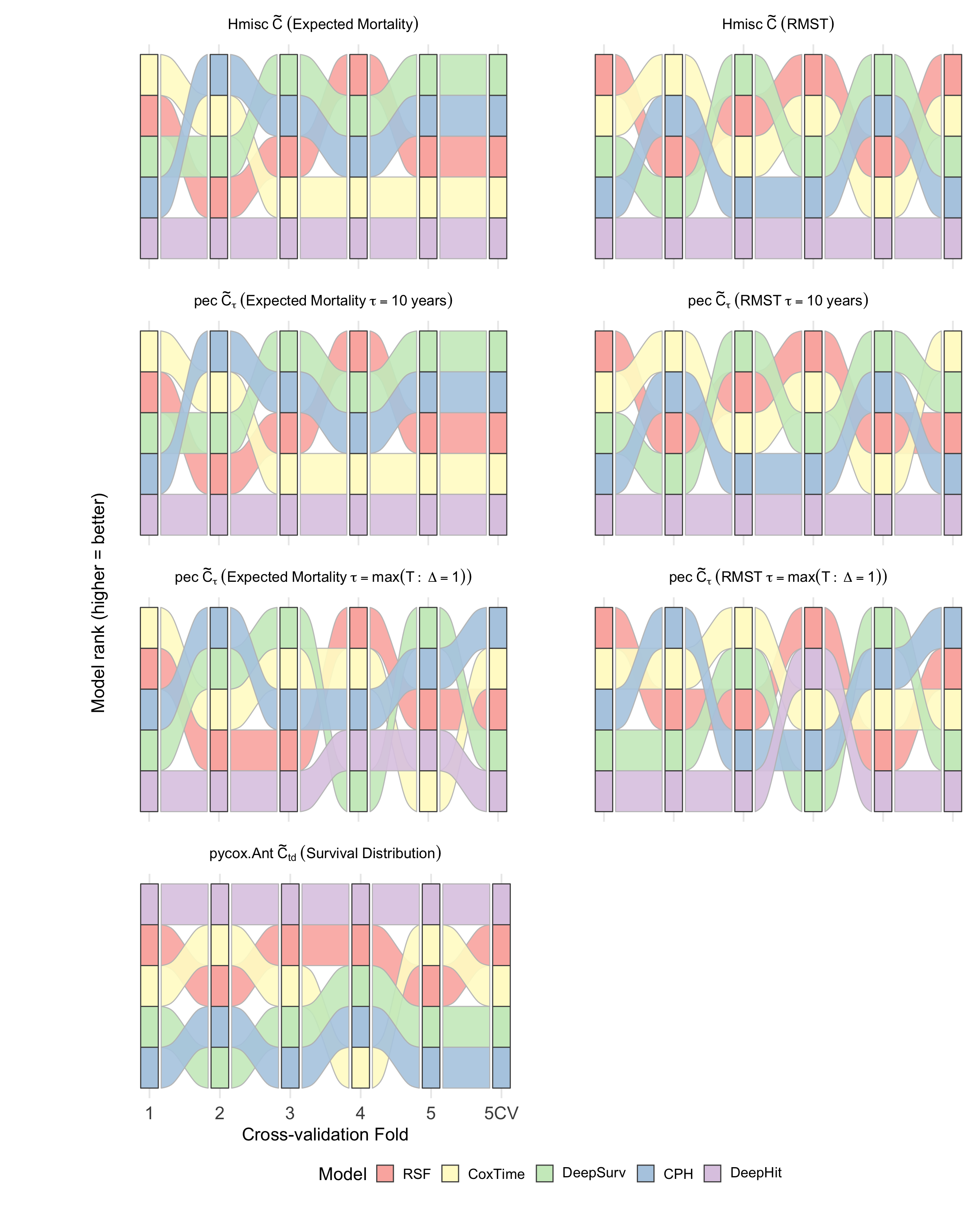
  Figure 4: Model ranking across CV folds based on different C-index estimates, illustrating the instability of rankings under different definitions and transformations.

Simulation Studies: Censoring Effects

The authors conduct semi-synthetic simulations to assess the impact of censoring and IPCW adjustment. Results show that:

• Without IPCW, the number of comparable pairs declines rapidly with increasing censoring, leading to biased estimates.
• IPCW stabilizes estimates but can be dominated by a few high-weight pairs if time truncation is not enforced.
• RMST-based transformations yield more stable and interpretable discrimination metrics compared to expected mortality.

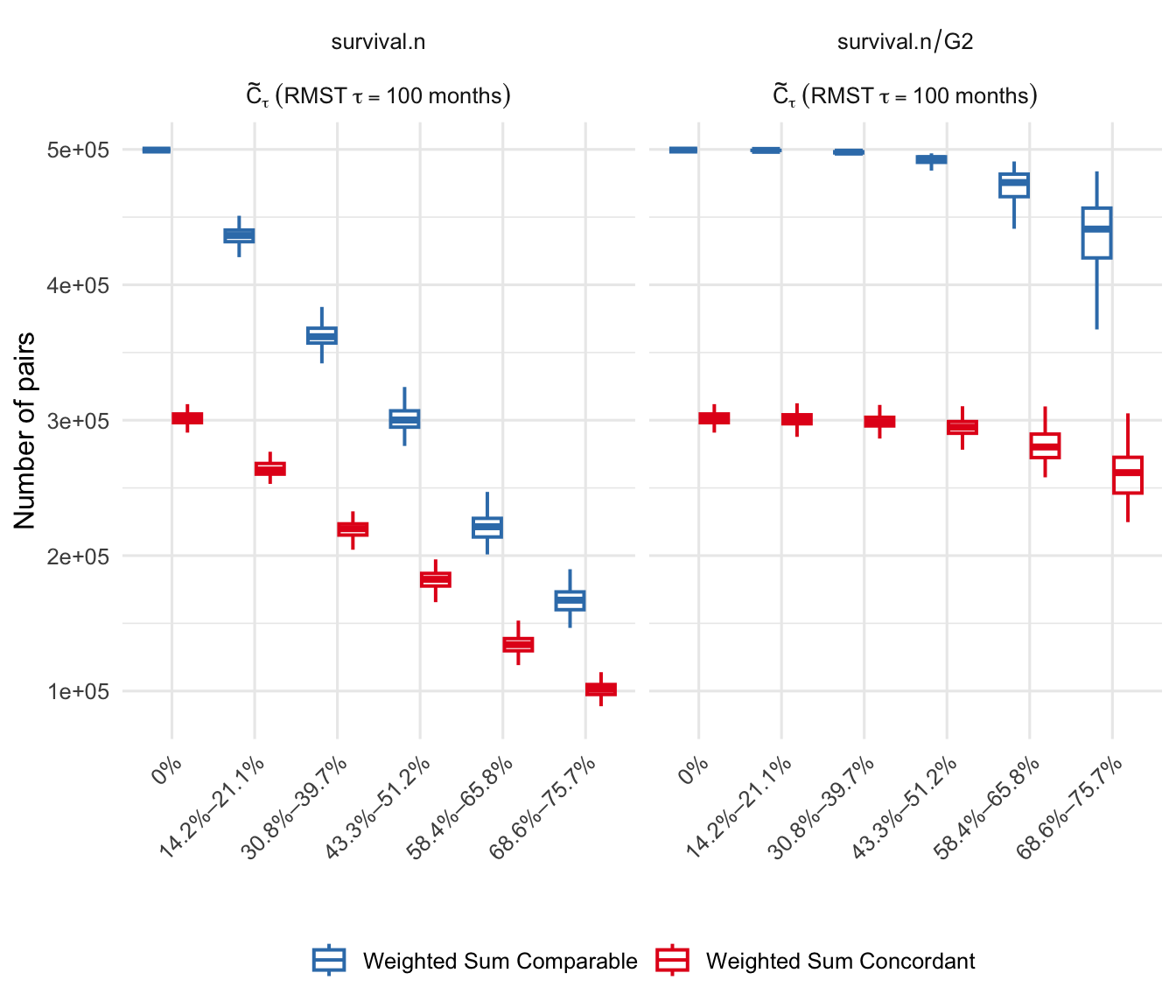
  Figure 5: Weighted sum of concordant and comparable pairs across increasing censoring levels, demonstrating the stabilizing effect of IPCW.

  

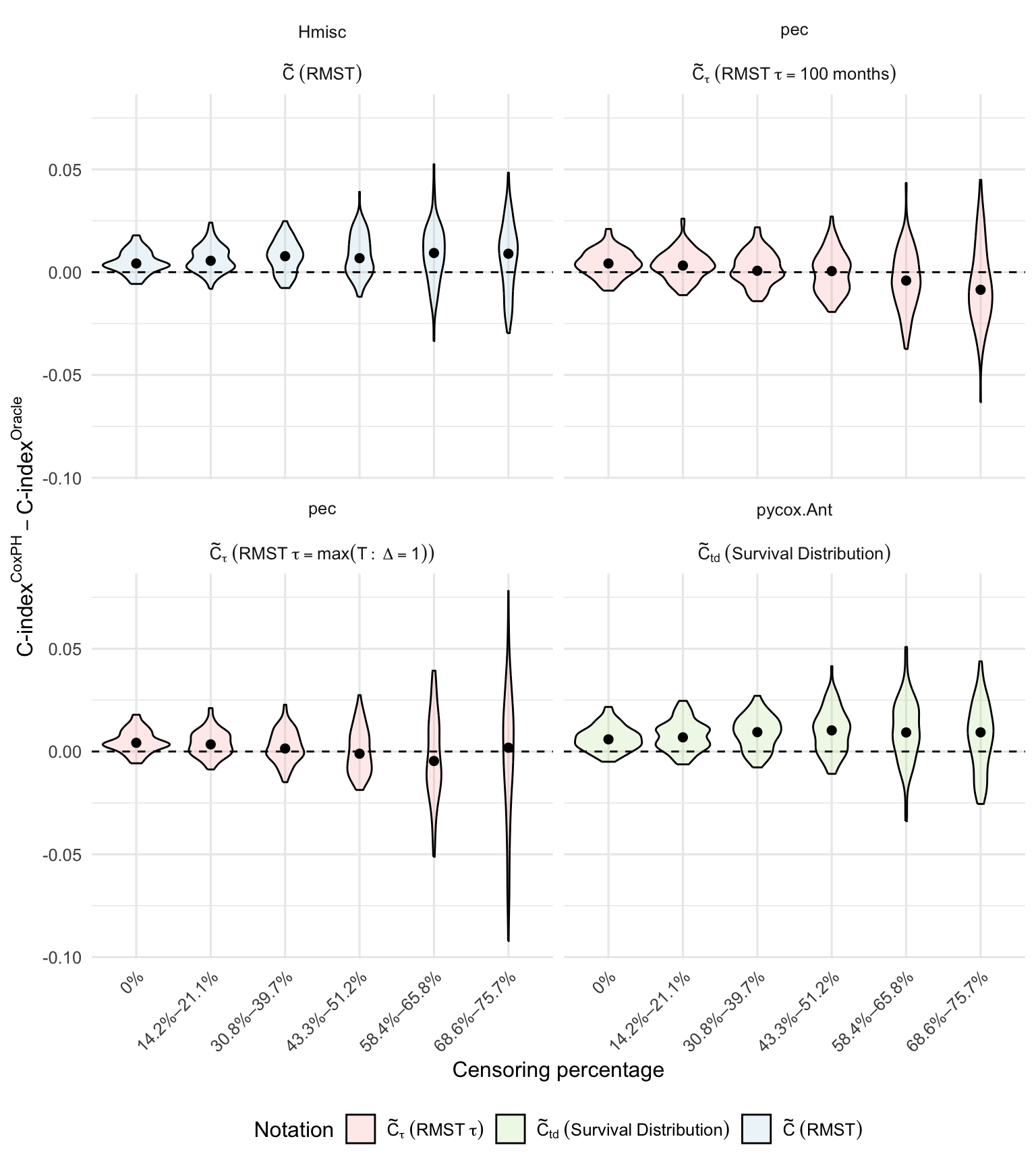
  Figure 6: Difference between C-index estimates and oracle values across increasing censoring, highlighting the bias-variance trade-off introduced by IPCW.

Practical and Theoretical Implications

The findings have several important implications:

• Reproducibility and transparency: Analysts must report not only the C-index value but also the estimator definition, software implementation, tie handling, censoring adjustment, and risk transformation used.
• Model selection and benchmarking: The choice of C-index variant and transformation can alter model rankings, potentially leading to "C-hacking" if selectively reported.
• Meta-analysis and external validation: Aggregating C-index values across studies without harmonizing implementations can yield invalid conclusions.
• Metric limitations: The C-index, regardless of implementation, does not capture calibration or the magnitude of risk differences, necessitating complementary metrics for clinical utility.

Future Directions

The paper suggests several avenues for future research:

• Development of standardized, well-documented C-index implementations with explicit options for tie handling, censoring adjustment, and risk transformation.
• Extension of the C-index multiverse analysis to competing risks and multi-state models.
• Investigation of alternative discrimination and calibration metrics, such as time-dependent AUC and proper scoring rules, especially for non-PH and deep learning models.
• Integration of calibration and clinical utility assessment into survival model evaluation pipelines.

Conclusion

This work rigorously demonstrates that the C-index is not a monolithic metric but a multiverse of definitions and implementations, each with distinct implications for model evaluation and selection. The authors provide unified documentation and practical guidelines for navigating this landscape, emphasizing the necessity of transparent reporting and harmonized benchmarking. The results underscore that stating "we calculated the C-index" is insufficient; detailed specification of the estimator, implementation, and transformation is essential for reproducibility and fair comparison.