Mathematical Computation and Reasoning Errors by Large Language Models (2508.09932v2)

Abstract: LLMs are increasingly utilized in AI-driven educational instruction and assessment, particularly within mathematics education. The capability of LLMs to generate accurate answers and detailed solutions for math problem-solving tasks is foundational for ensuring reliable and precise feedback and assessment in math education practices. Our study focuses on evaluating the accuracy of four LLMs (OpenAI GPT-4o and o1, DeepSeek-V3 and DeepSeek-R1) solving three categories of math tasks, including arithmetic, algebra, and number theory, and identifies step-level reasoning errors within their solutions. Instead of relying on standard benchmarks, we intentionally build math tasks (via item models) that are challenging for LLMs and prone to errors. The accuracy of final answers and the presence of errors in individual solution steps were systematically analyzed and coded. Both single-agent and dual-agent configurations were tested. It is observed that the reasoning-enhanced OpenAI o1 model consistently achieved higher or nearly perfect accuracy across all three math task categories. Analysis of errors revealed that procedural slips were the most frequent and significantly impacted overall performance, while conceptual misunderstandings were less frequent. Deploying dual-agent configurations substantially improved overall performance. These findings offer actionable insights into enhancing LLM performance and underscore effective strategies for integrating LLMs into mathematics education, thereby advancing AI-driven instructional practices and assessment precision.

• The paper demonstrates that LLMs exhibit distinct procedural and conceptual errors when solving math problems through detailed step-level analysis.
• It compares four models across arithmetic, algebra, and number theory tasks using both single-agent and dual-agent setups to highlight performance differences.
• Dual-agent collaboration significantly improves accuracy, suggesting effective strategies for enhancing AI reliability in educational assessments.

Mathematical Computation and Reasoning Errors by LLMs

Introduction

This paper presents a systematic evaluation of four LLMs—OpenAI GPT-4o, OpenAI o1, DeepSeek-V3, and DeepSeek-R1—on three categories of mathematical problem-solving tasks: arithmetic (multiplying two 5-digit numbers), algebra (solving quadratic word problems), and number theory (solving Diophantine equations). The paper emphasizes step-level reasoning errors, moving beyond standard benchmarks by constructing item models specifically designed to elicit LLM mistakes. Both single-agent and dual-agent (collaborative) configurations are analyzed, with solutions decomposed and labeled using a structured rubric to distinguish procedural, conceptual, and impasse errors. The findings provide actionable insights for improving LLM reliability in educational contexts, particularly for formative assessment and instructional feedback.

Experimental Design and Methodology

The dataset comprises three item models, each generating 10 instances per category, focusing on tasks known to challenge LLMs. The evaluation protocol involves:

• Single-agent setup: Each LLM independently solves problems step-by-step.
• Dual-agent setup: Two LLMs interact, cross-validate, and refine solutions collaboratively.

Solutions are segmented into logical steps and labeled as Conditionally Correct (CC), Procedural Error (PE), Conceptual Error (CE), or Impasse Error (IE). Labeling is performed by the o1 model and verified by human experts, with inter-rater reliability measured via Cohen’s $\kappa$.

Single-Agent Performance Analysis

Arithmetic: Multiplying Two 5-digit Numbers

The OpenAI o1 model achieves perfect accuracy across all iterations, while DeepSeek-V3 rapidly converges to perfect performance after initial errors. GPT-4o and DeepSeek-R1 lag significantly, with DeepSeek-R1 exhibiting an "overthinking" phenomenon—excessive intermediate reasoning that impedes correct solutions.

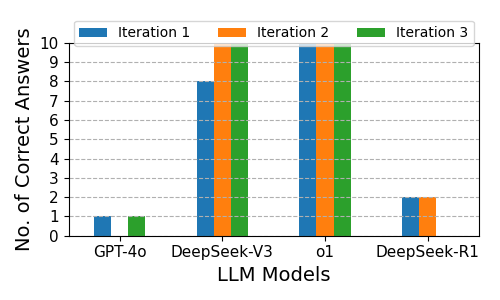
Figure 1: Correctness Across Three Iterations for the Multiplying Two 5-digit Numbers.

Algebra: Quadratic Word Problems

DeepSeek-V3, o1, and DeepSeek-R1 consistently solve all problems correctly. GPT-4o shows moderate performance, with a slight decline in the final iteration.

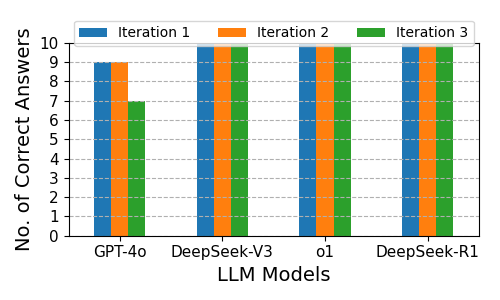
Figure 2: Correctness Across Three Iterations for Solving Algebraic Word Problems Involving Quadratic Equations.

Number Theory: Diophantine Equations

The o1 model outperforms all others, followed by DeepSeek-V3 and DeepSeek-R1. GPT-4o demonstrates the lowest accuracy.

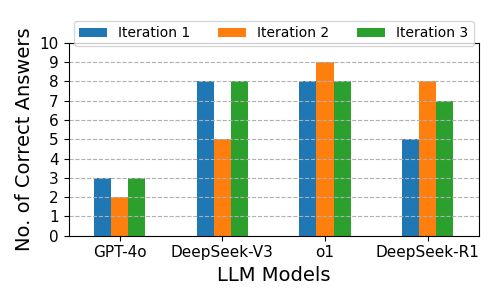
Figure 3: Correctness Across Three Iterations for Solving Diophantine equations.

Step-Level Error Analysis

Step-level labeling reveals that procedural errors (PE) are the most frequent and impactful, especially for GPT-4o and DeepSeek-R1. Conceptual errors (CE) are less common but present in DeepSeek models on number theory tasks. Notably, some incorrect final answers occur without identifiable step-level errors, highlighting the vulnerability of LLMs to subtle numerical inaccuracies due to token-based prediction rather than explicit computation.

Figure 4: Frequencies of Step Labels in Math Tasks (Where LLMs Stumble).

Cohen’s $\kappa$ for step-level annotation reliability is 0.366 for GPT-4o (fair agreement) and 0.737 for o1 (substantial agreement), indicating that models with stronger mathematical competence yield more dependable formative assessment.

Dual-Agent Collaboration

Dual-agent configurations substantially improve accuracy across all problem types. For arithmetic, GPT-4o’s correct answers increase from 2 (single-agent) to 14 (dual-agent). For algebra, both models achieve perfect accuracy. For number theory, DeepSeek-V3 reaches perfect accuracy, and GPT-4o nearly doubles its performance. These results corroborate prior findings that collaborative LLMs can replicate key benefits of human teamwork, such as cross-validation and emergent reasoning.

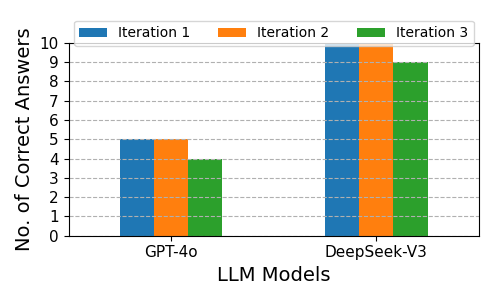
Figure 5: Dual-agent Correctness Across Three Iterations for Multiplying Two 5-digit Numbers.

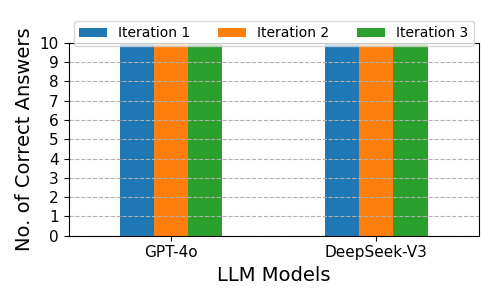
Figure 6: Dual-agent Correctness Across Three Iterations for Solving Algebraic Word Problems Involving Quadratic Equations.

Figure 7: Dual-agent Correctness Across Three Iterations for Solving Diophantine equations.

Implications and Future Directions

The paper demonstrates that reasoning-enhanced LLMs (e.g., o1) are more reliable for step-level annotation and formative assessment. Dual-agent collaboration offers a robust mechanism for error reduction and improved solution quality. The findings suggest several avenues for future research:

• Prompt engineering: Explicit step-by-step instructions may reduce procedural errors, especially in arithmetic.
• Tool integration: Delegating computation to external engines (calculators, CAS) while LLMs handle reasoning could mitigate token-based numerical inaccuracies.
• Rubric refinement: Developing more granular error taxonomies may uncover additional insights into LLM failure modes.
• Scaling datasets: Expanding item models and instances will improve generalizability and robustness of evaluation.
• Independent labeling: Future studies should compare LLM and human annotation as independent processes to further validate reliability.

Limitations

The dataset is limited to three item models and a small number of instances. The rubric is general; finer-grained categories may reveal more nuanced error patterns. Human verification of LLM labeling was not independent, and only a subset of commercial models was tested due to resource constraints.

Conclusion

This work provides a rigorous framework for evaluating LLM mathematical reasoning, highlighting the strengths of reasoning-enhanced models and collaborative agent paradigms. The publicly released dataset, coding rubric, and benchmarking protocol equip researchers and practitioners to diagnose procedural and conceptual breakdowns, informing the design of AI-driven instructional and assessment systems. Future research should focus on expanding problem coverage, refining error analysis, and integrating LLMs with computational tools to advance pedagogically sound, classroom-ready AI for mathematics education.