Combinative Matching for Geometric Shape Assembly (2508.09780v1)

Abstract: This paper introduces a new shape-matching methodology, combinative matching, to combine interlocking parts for geometric shape assembly. Previous methods for geometric assembly typically rely on aligning parts by finding identical surfaces between the parts as in conventional shape matching and registration. In contrast, we explicitly model two distinct properties of interlocking shapes: 'identical surface shape' and 'opposite volume occupancy.' Our method thus learns to establish correspondences across regions where their surface shapes appear identical but their volumes occupy the inverted space to each other. To facilitate this process, we also learn to align regions in rotation by estimating their shape orientations via equivariant neural networks. The proposed approach significantly reduces local ambiguities in matching and allows a robust combination of parts in assembly. Experimental results on geometric assembly benchmarks demonstrate the efficacy of our method, consistently outperforming the state of the art. Project page: https://nahyuklee.github.io/cmnet.

• The paper introduces combinative matching that models both identical surface shape and inverse volume occupancy to improve assembly accuracy.
• It employs equivariant neural networks for orientation alignment and transformation estimation to resolve local ambiguities in fragmented shapes.
• Empirical results show lower CRD and Chamfer Distance, demonstrating superior performance over conventional methods in challenging scenarios.

Combinative Matching for Geometric Shape Assembly

Introduction

The paper "Combinative Matching for Geometric Shape Assembly" (2508.09780) introduces a novel approach to geometric shape assembly. This method is significant in fields such as archaeology, medical imaging, robotics, and industrial manufacturing where reconstructing objects from fragmented parts is critical. The traditional reliance on identifying identical surfaces is insufficient due to issues like local ambiguities and the intrinsic properties needed for assembly rather than mere registration.

The authors propose a new shape-matching methodology, termed combinative matching, which explicitly models both 'identical surface shape' and 'opposite volume occupancy'. Unlike conventional approaches that focus solely on shape similarity, combinative matching aims to establish correspondences based on these two distinct properties. By doing so, it facilitates the learning to align regions in rotation and estimate shape orientations through equivariant neural networks, significantly reducing local ambiguities and enabling more robust combinations of parts.

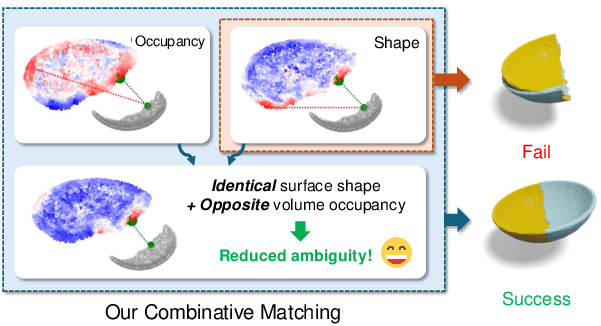
Figure 1: Combinative matching explicitly models identical surface shape and opposite volume occupancy for interlocking shapes.

Methodology

Combinative Matching

At the core of this approach is the concept of combinative matching. The methodology involves aligning orientations consistently across mating surfaces and ensuring that while surface shapes match (appear identical), the volume occupancy is inversely related to facilitate a stable interlock. This dual focus on surface resemblance and volumetric complementarity mirrors construction techniques like dovetail joints in civil engineering.

Equivariant Network Architecture: The model uses equivariant neural networks to predict and align local shape orientations. This alignment allows subsequent shape and occupancy features to be meaningfully compared, ensuring resilience against random transformations.

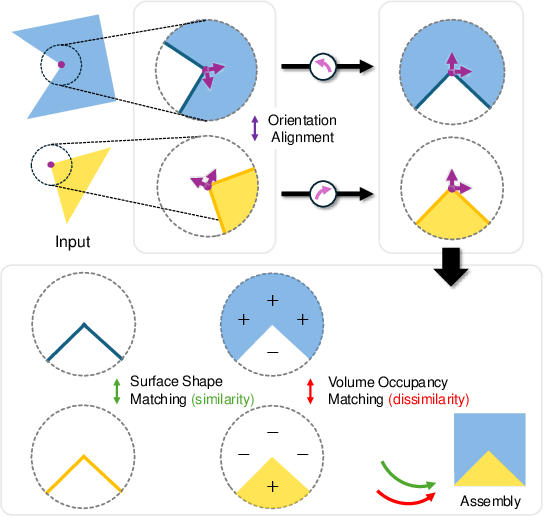
Figure 2: Main concept of combinative matching showcases complementary learning of shape and occupancy.

Network Architecture

The network architecture incorporates several components:

1. Feature Extraction and Orientation Alignment: Using VN-EdgeConvs, the network extracts rotation-equivariant features and hypothesizes local orientations. This results in shear-invariant representations required for subsequent matching tasks.
2. Surface Shape and Volume Occupancy Matching: The network contains distinct branches for processing shape and occupancy. Shape matching relies on appearance features, while occupancy matching leverages inverse volume relations to capture interlocking characteristics.
3. Transformation Estimation: By constructing a cost matrix integrating both shape and occupancy features, optimal correspondences are found using an OT layer, followed by SVD for estimating transformation parameters.

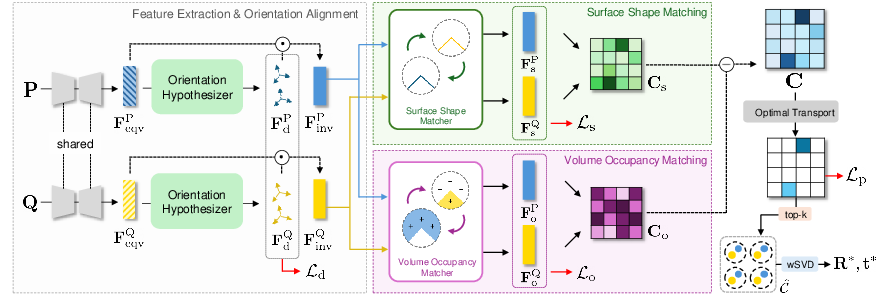
   Figure 3: Overall architecture displaying core components for feature extraction, shape matching, and transformation estimation.

Results and Analysis

The proposed approach was evaluated on a large-scale geometric assembly dataset, Breaking Bad, demonstrating its efficacy over existing baseline methods. The results highlighted significant improvements in assembly accuracy, particularly in scenarios with low surface overlap and high visual ambiguity.

Performance Metrics:

• CRD and CD: The combinative method consistently achieved lower CoRrespondence Distance (CRD) and Chamfer Distance (CD), indicative of superior assembly accuracy.
• Rotation and Translation Estimation: The method showed reduced RMSE for rotation and translation parameters, emphasizing its robustness in transforming random initial alignments to correct configurations.

In qualitative comparisons, the approach effectively resolved local ambiguities that plagued shape-based methods, as illustrated by the precise alignment of mating parts.

Figure 4: Visualization of learned orientations demonstrating efficacy in alignment across mating surfaces.

Discussion and Implications

The introduction of combinative matching offers a robust solution to geometric shape assembly by integrating surface resemblance with volumetric complementarity. This dual-model approach expands the scope of applications in AI where precise assembly from disparate parts is vital.

Future Directions:

1. Expanded Capacities: Future iterations could integrate additional properties like texture or color cues to further disambiguate complex assemblies.
2. Scalability: As AI systems increasingly move towards more complex environments, scalability in addressing larger multi-part assemblies needs exploration.
3. Generalization: While the method demonstrates promising results, extending its applicability across varied domains and data types remains an area of potential enhancement.

Conclusion

The paper presents a significant advancement in the field of geometric shape assembly. By accounting for both identical surface shape and opposite volume occupancy, combinative matching establishes a framework that improves accuracy and reliability in reconstructing fragmented structures. This methodology's robust performance across benchmarks signifies its potential as a foundational component in future AI assembly systems.