Functional Connectivity Graph Neural Networks (2508.05786v1)

Abstract: Real-world networks often benefit from capturing both local and global interactions. Inspired by multi-modal analysis in brain imaging, where structural and functional connectivity offer complementary views of network organization, we propose a graph neural network framework that generalizes this approach to other domains. Our method introduces a functional connectivity block based on persistent graph homology to capture global topological features. Combined with structural information, this forms a multi-modal architecture called Functional Connectivity Graph Neural Networks. Experiments show consistent performance gains over existing methods, demonstrating the value of brain-inspired representations for graph-level classification across diverse networks.

• The paper proposes a graph neural network framework that integrates functional connectivity via persistent graph homology to capture global topological features alongside structural data.
• The novel Functional Connectivity Block comprises connectivity and topological modules that efficiently derive functional embeddings from brain-inspired metrics.
• The framework significantly improves classification performance across diverse datasets, demonstrating the benefits of uniting neuroscience insights with GNN methodologies.

Functional Connectivity Graph Neural Networks

The paper "Functional Connectivity Graph Neural Networks" (2508.05786) introduces a novel graph neural network (GNN) framework that integrates structural and functional connectivity modalities inspired by brain imaging. This approach uses a functional connectivity block (FCB) based on persistent graph homology (PGH) to capture global topological features, complementing the traditional structural information utilized by GNNs.

Introduction

The study draws inspiration from neuroscience, where brain imaging techniques like fMRI and dMRI reveal insights into localized specialization and global integration through structural and functional connectivity. This synergy enables effective information processing and adaptability in biological networks.

Traditional GNNs emphasize local structural connectivity, relying on adjacent node interactions, which may limit their ability to capture inherent functional architectures shaping real-world networks. The integration of functional connectivity in GNNs aims to overcome these limitations by providing complementary learning signals that enhance graph-level classification.

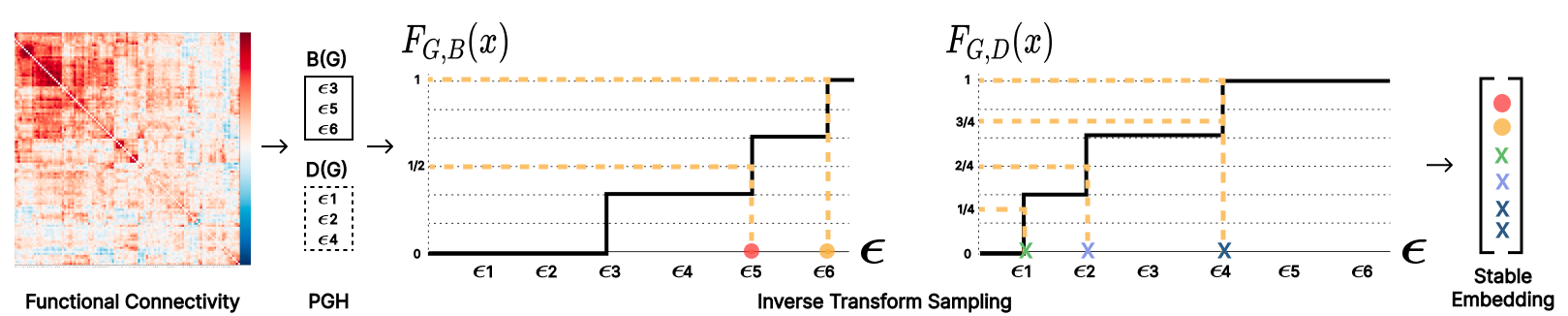
Figure 1: A schematic of the functional connectivity block illustrating the extraction of topological invariants using persistent graph homology.

Functional Connectivity Block

The functional connectivity block consists of two core modules:

1. Connectivity Feature Module: This module processes structural graphs to compute functional connectivity based on node feature correlations, using Pearson correlation due to its efficiency and interpretability.
2. Topological Feature Module: This module employs PGH to derive stable topological representations of graphs, capturing persistence diagrams that represent birth and death values of graph features across filtration values. These representations enable scalable learning from dense functional connectivity matrices.

   Figure 2: Graph filtration process illustrating the birth and death of graph features.

Functional Connectivity GNNs

The proposed FC-GNN architecture involves parallel processing pipelines for functional and structural graph representations:

• Functional Representation Learning: Using embeddings derived from PGH, topological features are processed with either a multi-layer perceptron (MLP) or a 1D convolutional neural network (1D-CNN) for effective feature extraction.
• Structural Representation Learning: Traditional GNNs leverage message-passing frameworks to capture structural connectivity, aggregating node-level features into comprehensive graph-level embeddings.
• Integration of Modalities: Functional and structural embeddings are fused using either concatenation or element-wise addition to leverage complementary signals for classification tasks.

  Figure 3: Architecture diagram of the functional connectivity graph neural networks illustrating the parallel pipelines for functional and structural features.

Applications in Graph-Level Classification

The FC-GNN framework was evaluated on various datasets spanning biological and social domains, demonstrating substantial accuracy improvements over single-modality GNNs. The incorporation of functional connectivity consistently enhanced performance across different architectures and dataset complexities, confirming the universal applicability of brain-derived connectivity principles.

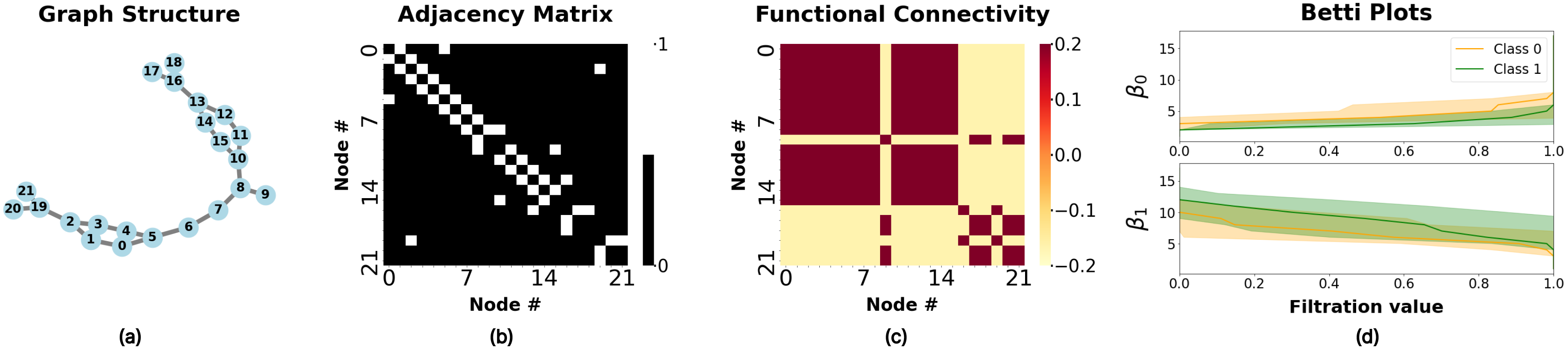
Figure 4: Visualization of MUTAG dataset representative showcasing structural and functional connectivity features.

Conclusion

This research advances graph representation learning by integrating brain-inspired functional connectivity into versatile GNN architectures. It provides an effective methodology for capturing both local and global network patterns across diverse domains, offering significant performance improvements in graph-level classification tasks. The approach translates principles from neuroscience into generalized graph learning strategies, solidifying the role of functional topology in advancing computational models and applications in complex network analysis.