What are you sinking? A geometric approach on attention sink (2508.02546v1)

Abstract: Attention sink (AS) is a consistent pattern in transformer attention maps where certain tokens (often special tokens or positional anchors) disproportionately attract attention from other tokens. We show that in transformers, AS is not an architectural artifact, but it is the manifestation of a fundamental geometric principle: the establishment of reference frames that anchor representational spaces. We analyze several architectures and identify three distinct reference frame types, centralized, distributed, and bidirectional, that correlate with the attention sink phenomenon. We show that they emerge during the earliest stages of training as optimal solutions to the problem of establishing stable coordinate systems in high-dimensional spaces. We show the influence of architecture components, particularly position encoding implementations, on the specific type of reference frame. This perspective transforms our understanding of transformer attention mechanisms and provides insights for both architecture design and the relationship with AS.

• The paper reveals the geometric necessity of attention sinks by identifying centralized, distributed, and bidirectional reference frames in transformer models.
• It provides a detailed mathematical formulation showing how attention weights converge into sparse, distinct patterns using threshold metrics.
• The paper demonstrates that optimizing architecture-specific loss functions can leverage attention sinks to enhance model efficiency and cross-architecture transfer.

What Are You Sinking? A Geometric Approach on Attention Sink

Introduction to Attention Sinks

The concept of "attention sink" (AS) within transformer models refers to a pattern where certain tokens, often special or positional anchors, disproportionately attract attention across transformer attention maps. This paper argues that AS is not an incidental byproduct of transformer architecture, but rather a geometric necessity. Specifically, attention sinks are viewed as manifestations of reference frames that anchor representation spaces, facilitating stable geometric relationships in high-dimensional parameter spaces. The identification and understanding of these sinks reveal insights into the operation of transformers and suggest new directions for architecture design and optimization.

Understanding Reference Frames

Reference frames within transformers are classified into three types based on their geometric organization:

1. Centralized Reference Frames: These frames establish a single dominant reference point, acting as a universal origin within the representation space. Such frames are commonly found in decoder-only architectures using standard Rotary Position Embedding (RoPE), where beginning-of-sequence tokens like "[BOS]" become central anchors.
2. Distributed Reference Frames: In these frames, multiple tokens serve as reference points, creating a flexible and localized coordinate system. Distributed frames emerge in architectures with modified positional encodings, like NTK-aware RoPE. This setup allows for multiple semi-distributed anchoring tokens, promoting adaptability and context-rich processing.
3. Bidirectional Reference Frames: Found in encoder-based models with absolute position embeddings, bidirectional frames develop dual anchors at both the start and end of sequences, enabling the network to handle bidirectional context effectively.

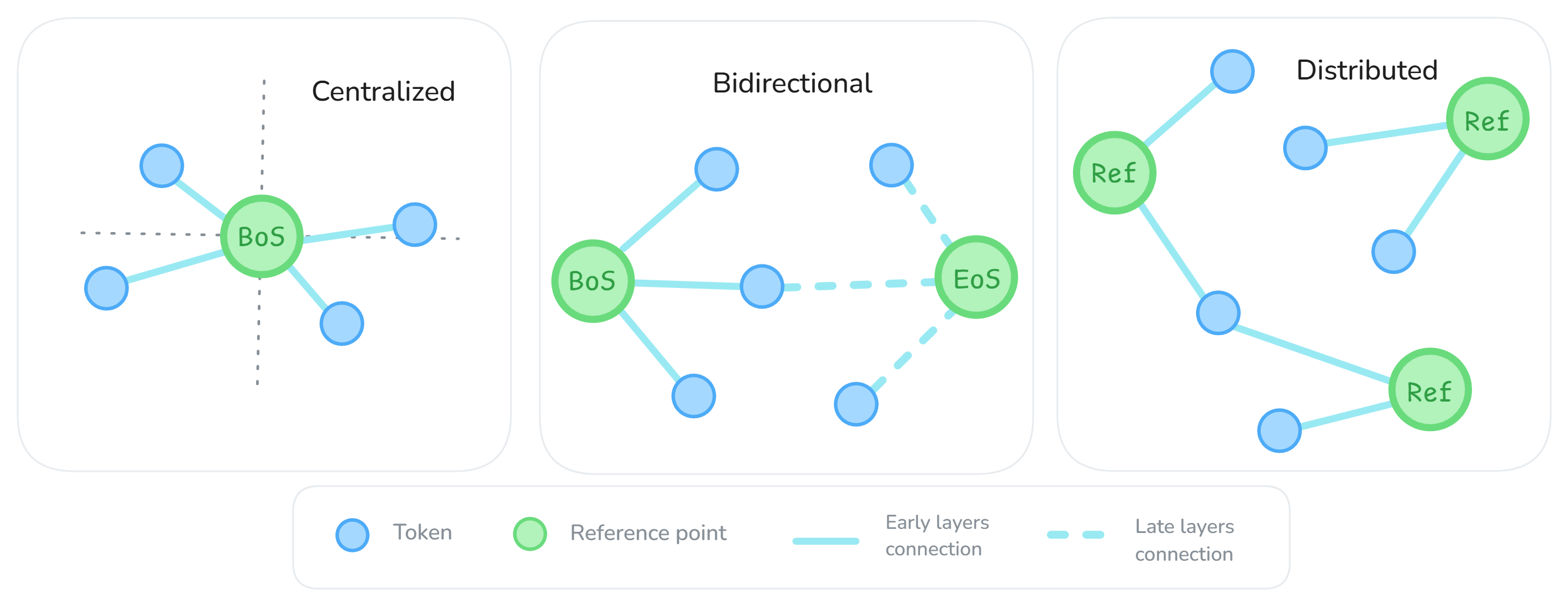
   Figure 1: Geometric interpretation of reference frames: (left) centralized frame with a single dominant reference point serving as a universal origin; (center) distributed frame with multiple weaker reference points creating a flexible coordinate system; (right) bidirectional frame with a dual-anchor structure and layer-wise specialization.

Mathematical Formalization of Attention Sinks

The emergence of reference frames is supported by rigorous mathematical formulations. Attention weights are dictated by the softmax function applied over dot products computed from query ($\mathbf{q}$) and key ($\mathbf{k}$) vectors. This operation confines the weights to the probability simplex, essentially encoding a constrained optimization problem that naturally leads to sparse and distinct concentration of attention—a pivotal characteristic of reference frames.

Each attention sink can be interpreted through mathematical encapsulation as follows:

$$\text{sink}(j) = \left[ \frac{1}{n}\sum_{i=1}^{n} \mathbb{1}_{\lbrace \alpha_{ij} \ge \tau \rbrace} \right] \ge \gamma$$

Here, $\alpha_{ij}$ denotes attention weights, $\tau$ represents a percentile threshold, and $\gamma$ is a frequency threshold metric ensuring robust detection of sinks.

Dynamic Formation and Optimization Impact

Reference frames arise not through explicit encoding but through self-organization facilitated by gradients converging towards optimal solutions influenced by architecture-specific inductive biases. Importantly, the formation of these frames can be optimized using loss functions tailored to highlight architecture-specific traits:

$$\mathcal{L} = \text{Loss Function influenced by Inductive Bias} (\mathcal{B})$$

This guides the natural convergence of the geometry towards specific frame types, highlighting the underlying robustness and adaptability of transformer architectures.

Practical Implications and Conclusion

The geometric perspective of attention sinks aligns strongly with real-world implementations, offering foundational insights for designing better AI models. By structuring reference frames strategically, architects can influence the adaptability, efficiency, and precision of AI models in representing and processing high-dimensional data. Predominantly, these findings promote an understanding of transformers beyond isolated architectural phenomena, unifying concepts of alignment, reference geometry, and hierarchical information processing.

Given the frameworks established in this research, future advancements could focus on leveraging attention sinks as structural anchors during transfer learning to optimize cross-architecture knowledge transfer effectively. Conclusively, this paper lays the groundwork for continued exploration of transformer geometry, informing both theoretical approaches and pragmatic deployment strategies in AI applications.