Monte Carlo studies of the emergent spacetime in the polarized IKKT model (2507.18472v1)
Abstract: The IKKT matrix model has been investigated as a promising nonperturbative formulation of superstring theory. One of the recent developments concerning this model is the discovery of the dual supergravity solution corresponding to the model obtained after supersymmetry-preserving mass deformation, which is dubbed the polarized IKKT model. Here we perform Monte Carlo simulations of this model in the case of matrix size N = 2 for a wide range of the deformation parameter Omega. While we reproduce precisely the known result for the partition function obtained by the localization method developed for supersymmetric theories, we also calculate the observables, which were not accessible by previous work, in order to probe the spacetime structure emergent from the dominant matrix configurations. In particular, we find that the saddle point corresponding to the original IKKT model is smoothly connected to the saddle represented by the fuzzy sphere dominant at large Omega, whereas the dominant configurations become diverging commuting matrices at small Omega.
Summary
- The paper demonstrates that the polarized IKKT model at N=2 exhibits a continuous transition between fuzzy sphere and commuting matrix dominated saddles as the deformation parameter Ω varies.
- The paper employs Monte Carlo simulations with parallel tempering to accurately reproduce predictions from SUSY localization and one-loop effective theory across different regimes.
- The study reveals that the emergent spacetime structure deviates from the original IKKT model in the Ω→0 limit, offering insights into vacuum dominance in deformed matrix models.
Monte Carlo Analysis of Emergent Spacetime in the Polarized IKKT Model
Introduction and Theoretical Context
The IKKT matrix model, also known as the type IIB matrix model, is a nonperturbative formulation of superstring theory, posited to provide a constructive definition of second-quantized string theory in the large-N limit. The model is a large-N reduced version of 10D N=1 super Yang-Mills theory and is interpreted as the effective theory of D-instantons. A central question in this framework is the dynamical emergence of spacetime, specifically whether a (3+1)-dimensional spacetime can arise as a dominant eigenvalue distribution from the underlying (9+1)-dimensional theory.
Recent developments have focused on the so-called polarized IKKT model, a supersymmetry-preserving mass deformation of the original model. This deformation introduces a mass scale Ω, breaking the SO(10) symmetry to SO(3)×SO(7) and yielding classical solutions corresponding to su(2) representations, i.e., fuzzy spheres. The polarized model admits a dual supergravity description and, crucially, allows for exact computation of the partition function via SUSY localization.
This work presents a detailed Monte Carlo paper of the polarized IKKT model at N=2, systematically probing the emergent spacetime structure and the nature of the transition between different dominant matrix configurations as a function of Ω.
Model Definition and Saddle Point Structure
The action of the polarized IKKT model is given by the original IKKT action plus a SUSY-preserving deformation:
S=SIKKT+SΩ
where SIKKT involves 10 bosonic and 16 fermionic N×N traceless Hermitian matrices, and SΩ introduces the mass scale Ω and breaks the symmetry as described above.
At large Ω, the path integral is dominated by the fuzzy sphere saddle, corresponding to the N-dimensional irreducible representation of su(2). In the Ω→0 limit, the dominant configurations become diverging commuting matrices, and the partition function diverges as Z∼Ω−2(N−1) for N=2, in contrast to the finite partition function of the original IKKT model.
The effective action after integrating out fermions is
Seff(A)=Sb(A)−logPf(M(A))
and the saddle-point equation is
0=dAdSeff
The analysis reveals two classes of saddle points: the fuzzy sphere saddle (dominant at large Ω) and the commuting matrix saddle (dominant at small Ω). The transition between these regimes is smooth for N=2, with the unique saddle of the original model continuously connected to the fuzzy sphere solution as Ω increases.
Monte Carlo Simulation Results
Monte Carlo simulations were performed for N=2 across a wide range of Ω, employing parallel tempering to reliably sample competing saddle points. The primary observable is the derivative of the partition function with respect to Ω, dlogZ(Ω)/dΩ=−⟨∂S/∂Ω⟩, which is directly accessible in simulation.
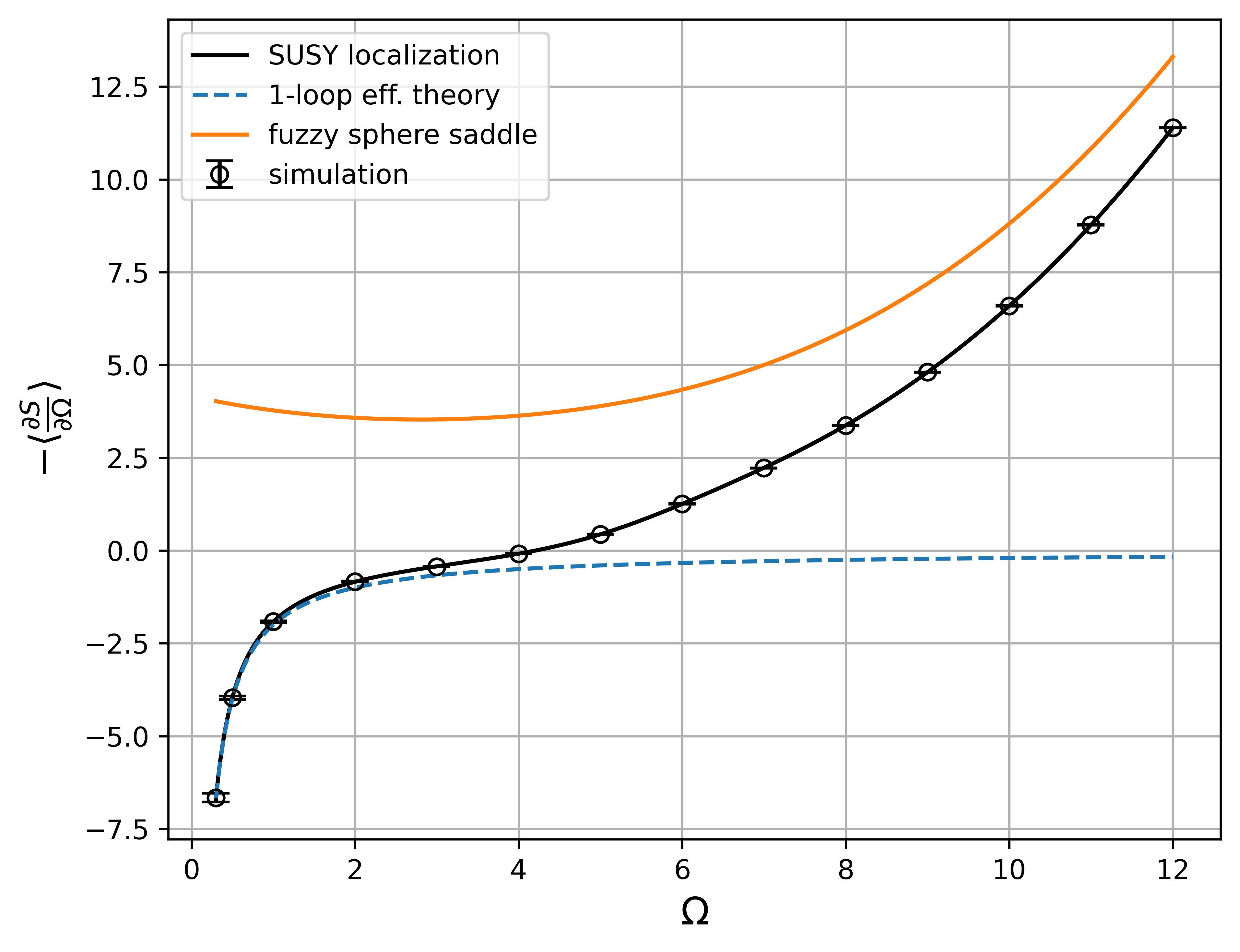
Figure 1: The derivative of the partition function dlogZ(Ω)/dΩ as a function of Ω, compared to SUSY localization, fuzzy sphere, and one-loop effective theory predictions.
The simulation results are in precise agreement with the SUSY localization method. At large Ω, the results approach the fuzzy sphere saddle prediction, while at small Ω, they match the one-loop effective theory, confirming the dominance of commuting matrices in this regime. Notably, dlogZ(Ω)/dΩ∼−2/Ω as Ω→0, consistent with the expected divergence of the partition function.
To probe the emergent spacetime structure, the extent of spacetime in the polarized (R3) and unpolarized (R7) directions was measured:
ρ3=tr(Aa)2,ρ7=tr(AI)2
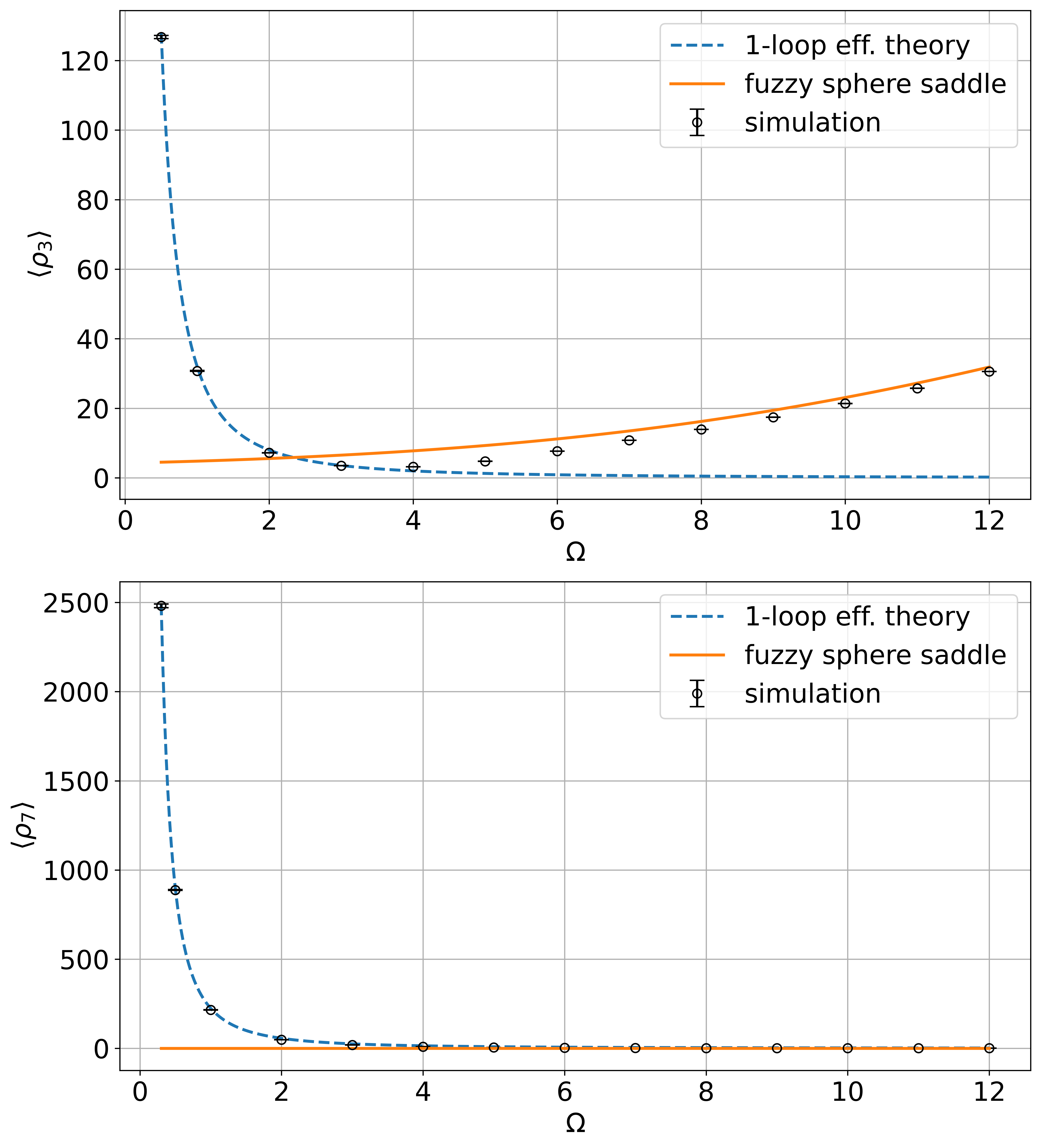
Figure 2: The extent of spacetime R3 (polarized) and R7 (unpolarized) as functions of Ω, compared to fuzzy sphere and one-loop effective theory predictions.
At large Ω, R3 grows quadratically and R7 vanishes, as expected for the fuzzy sphere. At small Ω, both R3 and R7 grow rapidly, in agreement with the one-loop effective theory, confirming the dominance of commuting matrices.
The transition between these regimes is further elucidated by histograms of logρ3 and logρ7 for various Ω.
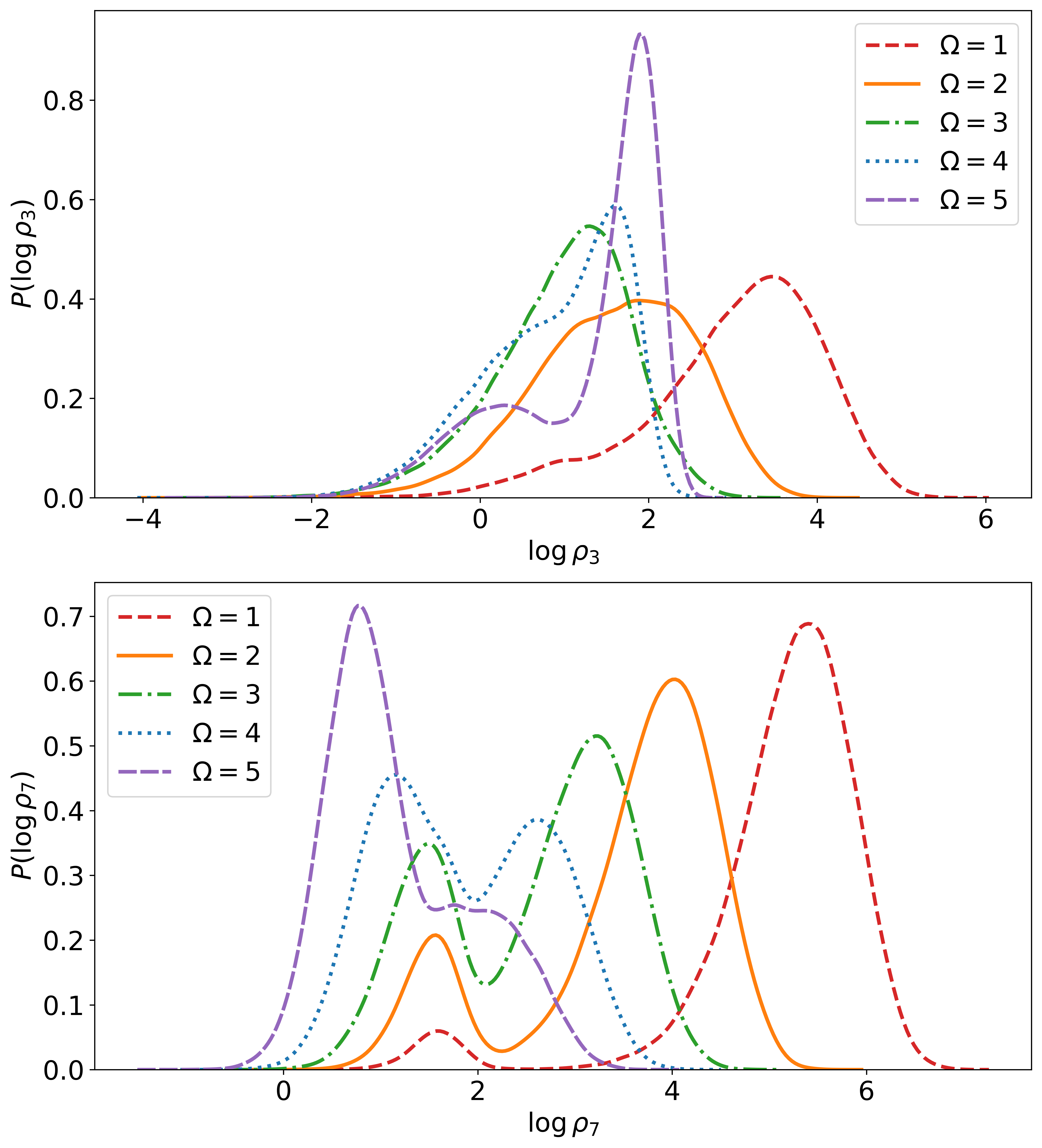
Figure 3: Histograms of logρ3 (top) and logρ7 (bottom) for Ω=1,2,…,5, showing the emergence and merging of double-peak structures.
At intermediate Ω∼4, double-peak structures appear in the histograms, indicating coexistence of the two types of dominant configurations. The observables remain continuous across the transition for N=2, in contrast to the sharp phase transition observed at larger N.
Implications and Theoretical Significance
A key finding is that the polarized IKKT model does not reduce to the original IKKT model in the Ω→0 limit, due to the dominance of new saddle points corresponding to diverging commuting matrices. This phenomenon is generic and not restricted to supersymmetric or fermionic systems; it can be illustrated by simple one-variable integrals with polynomial potentials, where a deformation introduces new minima that dominate the partition function in the small deformation limit.
This insight has broad implications for the paper of vacuum structure in quantum field theory and string theory. In the context of the string landscape, small deformations can lead to new dominant vacua, potentially altering the emergent spacetime and gauge symmetry content. The results also motivate further paper of SUSY mass deformations in Lorentzian versions of the IKKT model, where new expanding spacetime solutions may arise.
The technical achievement of reliably sampling both saddle points at small N using parallel tempering is notable, as it enables precise comparison with localization results and detailed exploration of the emergent geometry.
Conclusion
This paper provides a comprehensive Monte Carlo analysis of the polarized IKKT model at N=2, elucidating the transition between fuzzy sphere and commuting matrix saddle points as a function of the deformation parameter Ω. The results confirm the predictions of SUSY localization and one-loop effective theory, and reveal the geometric nature of the transition in the emergent spacetime structure. The observation that the original IKKT model is not recovered in the Ω→0 limit highlights the subtlety of vacuum dominance in deformed matrix models, with implications for the broader landscape of nonperturbative string theory and quantum gravity. Future work should extend these methods to larger N and to Lorentzian models, where richer phase structure and emergent geometries are anticipated.
Follow-up Questions
- How does the polarized deformation impact the emergence of specific spacetime dimensions in the IKKT model?
- What are the technical challenges in sampling the competing saddle points using parallel tempering in the Monte Carlo simulations?
- How do the simulation results validate the predictions from both SUSY localization and one-loop effective theory?
- What implications do these findings have for nonperturbative approaches in string theory and quantum gravity?
- Find recent papers about emergent spacetime in matrix models.
Related Papers
- Monte Carlo studies of supersymmetric matrix quantum mechanics with sixteen supercharges at finite temperature (2007)
- N=2 supersymmetric theories on squashed three-sphere (2011)
- The perturbative partition function of supersymmetric 5D Yang-Mills theory with matter on the five-sphere (2012)
- The Polarised IKKT Matrix Model (2024)
- Dynamical Compactification of Extra Dimensions in the Euclidean IKKT Matrix Model via Spontaneous Symmetry Breaking (2020)
- Emergent fuzzy geometry and fuzzy physics in $4$ dimensions (2016)
- Impact of Supersymmetry on Emergent Geometry in Yang-Mills Matrix Models II (2012)
- Inequivalence between the Euclidean and Lorentzian versions of the type IIB matrix model from Lefschetz thimble calculations (2025)
- Holography for the IKKT matrix model (2025)
- Statistical Physics of the Polarised IKKT Matrix Model (2025)
Authors (3)
alphaXiv
- Monte Carlo studies of the emergent spacetime in the polarized IKKT model (2 likes, 0 questions)