Advanced Space Mapping Technique Integrating a Shared Coarse Model for Multistate Tuning-Driven Multiphysics Optimization of Tunable Filters

Abstract: This article introduces an advanced space mapping (SM) technique that applies a shared electromagnetic (EM)-based coarse model for multistate tuning-driven multiphysics optimization of tunable filters. The SM method combines the computational efficiency of EM single-physics simulations with the precision of multiphysics simulations. The shared coarse model is based on EM single-physics responses corresponding to various nontunable design parameters values. Conversely, the fine model is implemented to delineate the behavior of multiphysics responses concerning both nontunable and tunable design parameter values. The proposed overall surrogate model comprises multiple subsurrogate models, each consisting of one shared coarse model and two distinct mapping neural networks. The responses from the shared coarse model in the EM single-physics filed offer a suitable approximation for the fine responses in the multiphysics filed, whereas the mapping neural networks facilitate transition from the EM single-physics field to the multiphysics field. Each subsurrogate model maintains consistent nontunable design parameter values but possesses unique tunable design parameter values. By developing multiple subsurrogate models, optimization can be simultaneously performed for each tuning state. Nontunable design parameter values are constrained by all tuning states, whereas tunable design parameter values are confined to their respective tuning states. This optimization technique simultaneously accounts for all the tuning states to fulfill the necessary multiple tuning state requirements. Multiple EM and multiphysics training samples are generated concurrently to develop the surrogate model. Compared with existing direct multiphysics parameterized modeling techniques, our proposed method achieves superior multiphysics modeling accuracy with fewer training samples and reduced computational costs.

• The paper introduces a novel surrogate modeling framework that leverages a shared electromagnetic coarse model to optimize multiple tuning states efficiently.
• It integrates neural network-based parameter and frequency mappings with a trust-region iterative strategy to reduce simulation costs and iterations.
• The method achieves significant runtime reductions and improved accuracy in complex multiphysics applications such as evanescent-mode cavity and waveguide filters.

Advanced Space Mapping with Shared Coarse Models for Multistate Multiphysics Optimization of Tunable Filters

Introduction and Context

The paper "Advanced Space Mapping Technique Integrating a Shared Coarse Model for Multistate Tuning-Driven Multiphysics Optimization of Tunable Filters" (2507.14220) presents a new surrogate modeling approach for the multiphysics optimization of microwave tunable filters with multiple tuning states. The method leverages space mapping (SM) techniques with a novel integration of a shared electromagnetic (EM) coarse model, allowing efficient and accurate design across coupled EM-thermal-mechanical domains. The primary contribution is a surrogate modeling architecture that enables simultaneous optimization for multiple tuning states, reducing data requirements from expensive multiphysics simulations via strategic use of EM-only simulations and neural network-based parameter mappings.

Surrogate Model Architecture

The proposed surrogate model consists of multiple "subsurrogate" models, each representing a specific tuning state of the filter. Crucially, all subsurrogates share a single, EM-based coarse model, capturing the common dependence on nontunable parameters, while two neural network mappings (parameter and frequency) are individually trained for each tuning state. The design parameter mapping transforms multiphysics space parameters to those compatible with the EM-only field, while the frequency mapping accounts for shifts in resonant behavior induced by, e.g., piezoelectric effects. This structure substantially reduces the number of required expensive high-fidelity simulations compared to approaches where completely independent surrogate models are trained for each tuning state.

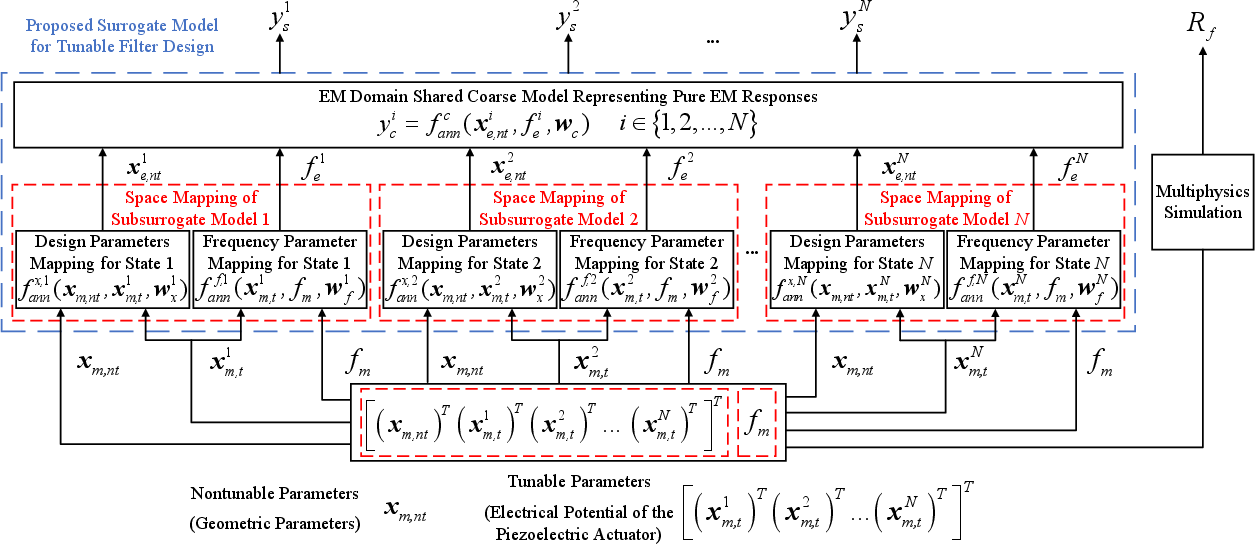
Figure 1: Structure of the proposed surrogate model for microwave tunable filter optimization with multiple sets of tuning states.

Parallel data generation is performed: EM coarse model data are produced via fast ANSYS HFSS simulations, while independent COMSOL Multiphysics runs generate training points for the high-fidelity (fine) subsurrogates. Orthogonal DOE sampling ensures efficient coverage of the design space at each trust-region iteration.

Figure 2: DOE-driven design parameter sample generation for EM single-physics (shared coarse model) and each multiphysics subsurrogate model.

Optimization and Training Strategy

The optimization leverages a two-stage ANN training process. First, the EM-based coarse model is trained with a larger set of EM simulation datapoints. Once this model reaches satisfactory error bounds, its weights are fixed. Next, the two mapping networks per tuning state are trained using multiphysics (MP) datapoints, minimizing the squared error between the mapped EM-predicted responses and the target multiphysics responses. A trust-region approach governs sample region updates, ensuring robust convergence. The process iteratively refines both the surrogate and design parameters until specified convergence criteria (norm-based or response-based) are met. The technique naturally scales to arbitrary $N$ tuning states, with a single shared coarse model amortizing EM simulation cost, and the computational burden of multiphysics data collection further mitigated by full parallelization.

Figure 3: Flowchart of the proposed tunable filter optimization technique using a novel surrogate model.

Numerical Demonstration: Evanescent-Mode Cavity Filter

The first benchmark is a piezoactuated evanescent-mode cavity filter. The structure's nontunable geometric parameters (width, length, gap) and tunable state (applied voltage) are managed as described. Frequency response objectives are set for two distinct tuning states (two voltage configurations).

Figure 4: Configuration of the tunable evanescent mode cavity filter using a piezoactuator.

The results indicate rapid convergence (3 iterations) to a design that meets both sets of $|S_{11}|$-based bandwidth requirements, with the EM-coarse/shared model reducing multiphysics data and runtime by over 27% compared to standard ANN-trained surrogate baselines. Notably, the approach achieves higher accuracy at lower cost and with fewer optimization iterations.

Figure 5: Comparison of the magnitude of $S_{11}$ for two input voltages with shared geometry; demonstrates voltage-driven tunability.

Figure 6: Structure of the proposed surrogate model for the tunable evanescent-mode cavity filter.

The comparison to monolithic ANN approaches unequivocally demonstrates the benefit of the shared-coarse/mapping model structure in sample efficiency and computational savings.

Figure 7: Magnitude (in decibels) of $S_{11}$ post-optimization confirms simultaneous satisfaction of dual tuning state criteria.

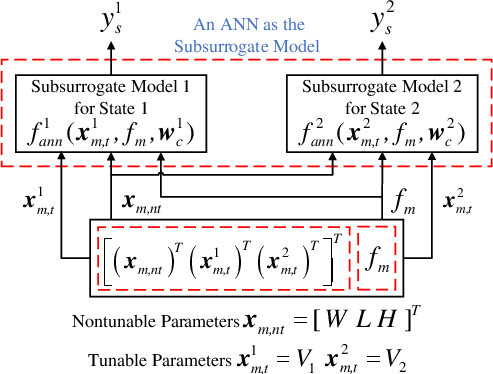
Figure 8: Structure of the surrogate model using an ANN model as the subsurrogate model for the tunable evanescent-mode cavity filter (non-shared-coarse baseline).

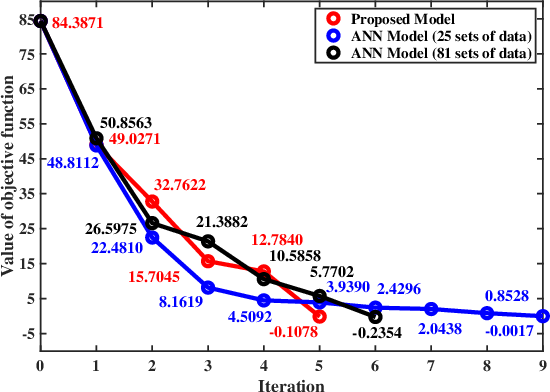
Figure 9: Values of the objective function through optimization; the proposed method converges more rapidly with lower final error.

Numerical Demonstration: Four-Pole Waveguide Filter

A second example tackles a multiphysics-optimized four-pole WR-75 waveguide filter with two piezoactuators, again using both nontunable mechanical parameters and multiple tunable voltages. The model efficiently optimizes three distinct tuning states by sharing the EM coarse model and parallelizing the mapping networks.

Figure 10: Structure of the tunable four-pole waveguide filter using a piezoactuator.

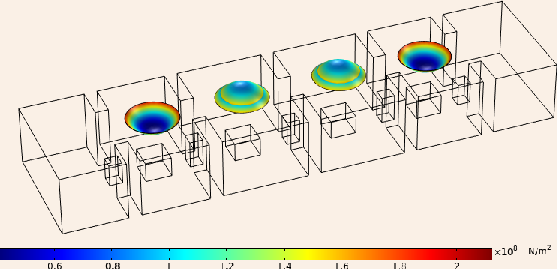
Figure 11: Deformed structure of the tunable four-pole waveguide filter caused by the input voltages.

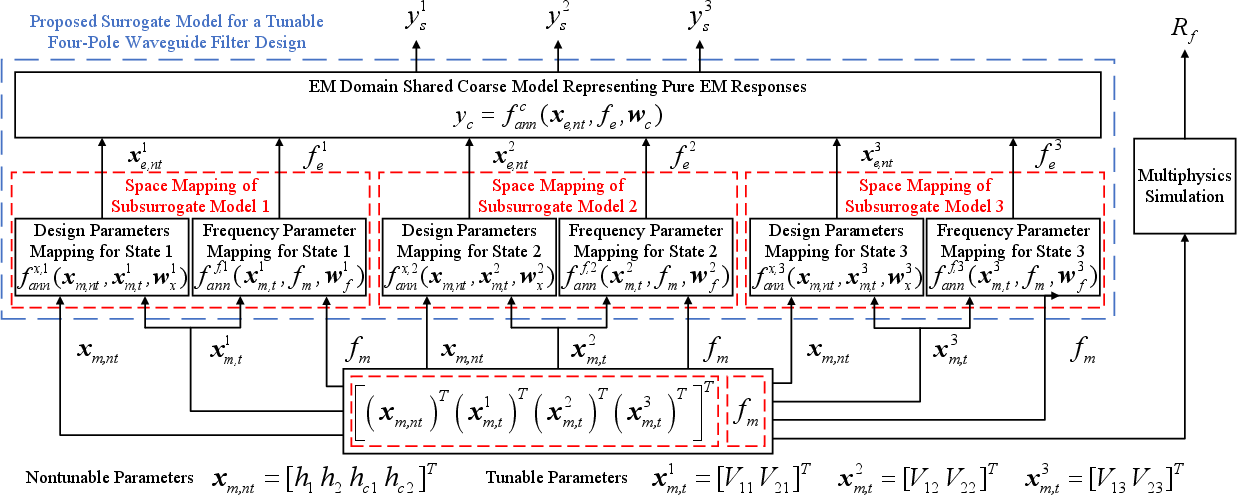
Figure 12: Structure of the proposed surrogate model for this tunable four-pole waveguide filter.

After five iterations, optimal solutions satisfy all three frequency/tuning state constraints. Compared to direct multiphysics ANN models, the method reduces runtime by up to 46%, and consistently achieves lower error with minimal data.

Figure 13: Magnitude (in decibels) of $S_{11}$ at each optimized tuning state validates simultaneous multi-state optimization.

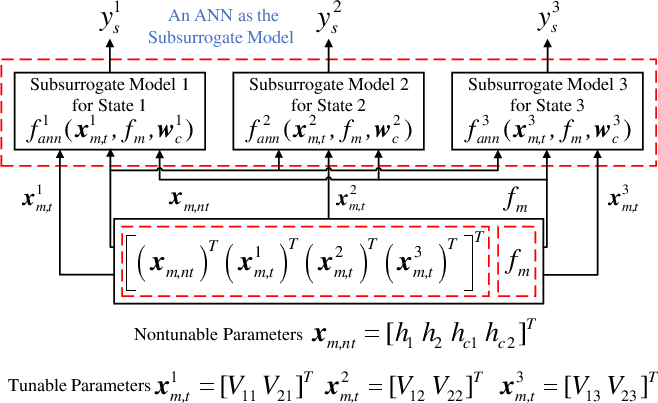
Figure 14: Structure of the surrogate model using an ANN model as the subsurrogate model for the tunable four-pole waveguide filter—comparison baseline.

Figure 15: Objective function trajectories show faster convergence and lower error for the proposed approach.

Theoretical and Practical Implications

The architecture decouples the expensive multiphysics simulation problem, amortizing high-fidelity sample costs and leveraging the fact that many nontunable variables impact all tuning states in similar ways. By using mapping networks to translate between EM-only and multiphysics response spaces, the surrogate model robustly addresses nonlinear, strongly coupled behaviors like piezoelectric deformation. The approach supports detailed device-level virtual prototyping where EM, structural, and thermal domains interact.

Practically, this method enables the routine, reliable design of high-performance tunable microwave filters, dramatically compressing simulation and design cycles. The model is extensible to higher-parameter-count problems, and can accommodate more complex multiphysics couplings and broader tuning ranges by increasing the number of subsurrogate channels. The ability to leverage distributed/parallel computation for data generation further extends its scalability.

Future Perspectives

Immediate research directions include extension to additional multiphysics domains (e.g., full thermal-electromechanical problems), incorporation of measurement data for model refinement, and extrapolative surrogate training. Methodological advances around transfer learning and physics-informed neural mapping architectures could further reduce sample counts and improve extrapolation. Integrating pole-zero transfer function models, as suggested by the authors, may address challenging initial point selection and robustly handle cases with highly nonlinear tuning-induced behavior shifts.

Conclusion

This work establishes a comprehensive surrogate modeling and optimization framework for tunable microwave filters under multiphysics constraints, achieving simultaneous design for multiple tuning states with minimal computational burden. Quantitative results robustly demonstrate both improved sample efficiency and superior accuracy over traditional ANN surrogate strategies, validated across complex, real-world filter architectures. The shared-coarse model with per-state mappings provides a scalable, generalizable template for multiphysics design automation, with ongoing relevance to next-generation RF, microwave, and photonic component optimization.