A Theory of Inference Compute Scaling: Reasoning through Directed Stochastic Skill Search (2507.00004v2)

Abstract: LLMs demand considerable computational, energy, and financial resources during both training and deployment. While scaling laws for training have guided much of the field's recent progress, inference costs now represent a significant and growing component of the overall resource burden, particularly for reasoning-focused models. Existing characterizations of compute-optimality that consider model size, dataset size, and inference tokens in isolation or in fixed combinations risk overlooking more efficient operating points. We introduce directed stochastic skill search (DS3), a general framework that represents inference as stochastic traversal over a learned skill graph. From a simplified yet expressive instantiation, we derive closed-form expressions for task success and compute cost across a wide range of inference strategies -- including chain-of-thought (CoT) and tree-of-thought (ToT) -- enabling comparative analysis as a function of task difficulty and model capability. To that end, we extend a prior first-principles tripartite graph framework of LLM training to incorporate inference, and separately bridge DS3 with empirical methods that characterize LLM scaling behavior. We theoretically recover empirically observed patterns, including: linear accuracy scaling with logarithmic compute; variation in preferred inference strategies as a function of task difficulty and model capability; emergent behavior elicited by reasoning even when performance plateaus under parameter scaling; and both best-of-N (BoN) and majority voting behavior captured within a unified analytical framework. By explicitly characterizing training-inference interdependencies, our framework deepens theoretical understanding and supports principled algorithmic design and resource allocation.

• The paper introduces DS3, a framework that models inference as a stochastic traversal over a latent skill graph to optimize compute costs.
• It compares inference strategies including chain-of-thought, tree-of-thought, Best-of-N, and majority voting to balance sequential and parallel reasoning.
• The framework unifies training and inference scaling, predicting emergent behaviors and guiding resource-efficient LLM deployment.

A Theory of Inference Compute Scaling: Reasoning through Directed Stochastic Skill Search

Introduction

This paper presents a comprehensive framework for understanding and optimizing the inference compute costs associated with LLMs, particularly those focused on reasoning tasks. As the demand for inference efficiency grows, this framework introduces Directed Stochastic Skill Search (DS3), which characterizes inference as a stochastic traversal over a learned skill graph.

DS3 Framework

The DS3 framework treats inference as a dynamic ensemble of sequential traces over a latent skill graph. Each trace explores skills required for task execution and is governed by stochastic transitions and outcomes. This structure allows modeling of inference strategies like chain-of-thought (CoT) and tree-of-thought (ToT), facilitating comparative analysis across task difficulty and model capabilities.

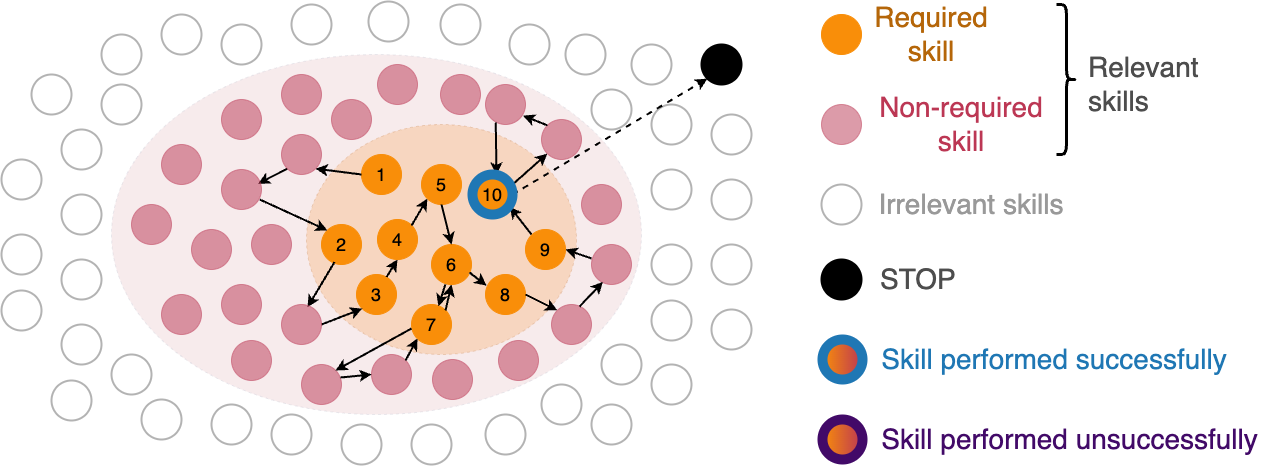
Figure 1: A directed stochastic skill search for a CoT policy, terminating upon completion of the final required skill.

Inference Strategies

The paper explores various inference strategies within the DS3 framework:

1. Chain-of-Thought (CoT): Involves sequential skill application and is suitable for tasks with high individual step success probabilities. The success probability is modeled as a negative binomial distribution over a given token budget.
2. Tree-of-Thought (ToT(1)): Introduces branching at skill nodes allowing parallel exploration, which enhances task completion probability by evaluating multiple paths simultaneously.
3. Best-of-N (Bo$N$): Utilizes multiple independent traces with an oracle verifier, optimizing the chance of task success through parallel sampling.
4. Majority Voting (MV): Selects the most frequently generated output among parallel samples, potentially saturating accuracy when aggregating votes across a population of tasks.

Each strategy is characterized by its compute cost composition, which includes parameter, attention, and evaluation-related components. The balance between sequential and parallel reasoning is crucial for optimizing resource allocation.

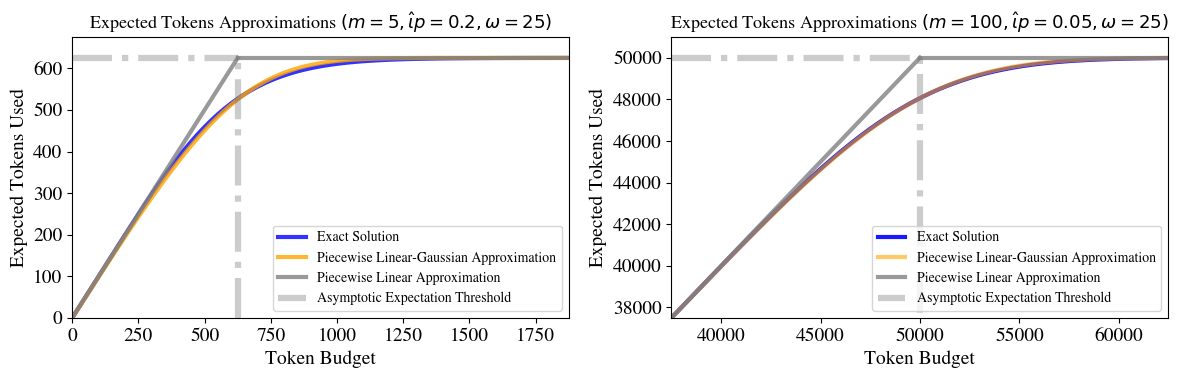
Figure 2: CoT expected token usage under capped inference budgets.

Unification with Training Scaling

The paper extends a prior hierarchical skill-text tripartite graph framework to incorporate inference compute scaling, integrating training and inference into a unified model. This approach facilitates analysis of how training compute impacts model capability, supporting principled algorithmic design and resource allocation.

The hierarchical model suggests updated patterns in inference with multiple solution strategies across hierarchical skill levels. The framework accurately predicts emergent behaviors, such as skill acquisition and composability, offering insights into task completion over varying levels and task types.

Figure 3: Contour plot of model accuracy under Chinchilla-style pretraining, showing total-compute-optimal allocations for a CoT policy.

Implications and Conclusion

This unified perspective challenges existing scaling laws by emphasizing the role of inference shaping the compute-optimal frontier. As LLMs scale, both training and inference capabilities need simultaneous optimization, reflecting their deeply interdependent dynamics. With Jevons-like effects emerging from efficiency gains, AI systems may witness sustained growth in inference demand.

The proposed DS3 framework offers a theoretical foundation with practical implications for improving the sustainability and efficiency of AI model deployment and operations, promoting innovation in inference methodologies.

In conclusion, DS3 provides a robust mechanism for understanding the intricate balance of training and inference, advancing the field towards efficiently harnessing the full potential of LLMs across diverse applications.

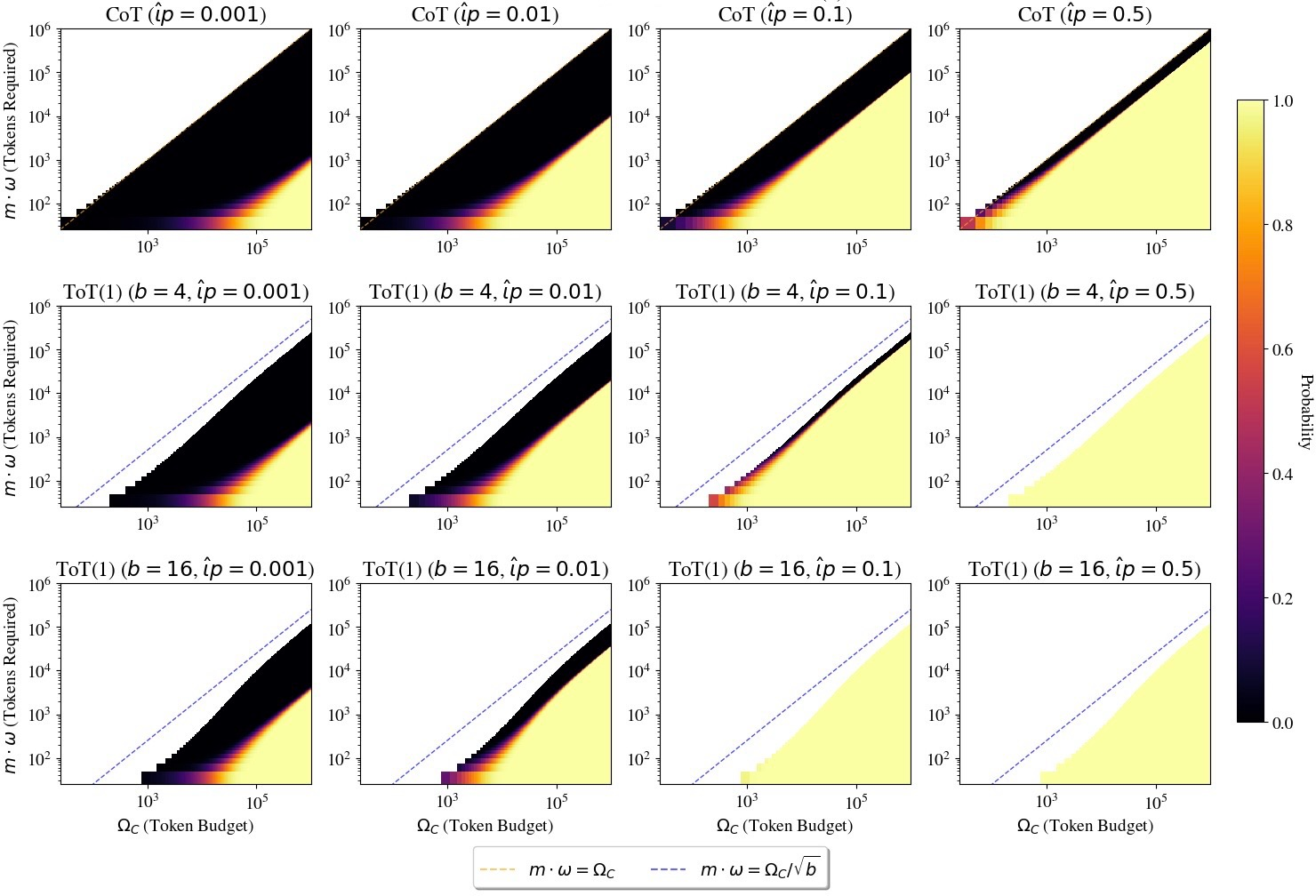
Figure 4: Success probabilities for CoT and ToT(1) across varying token budgets and numbers of required skills.