Latent Guided Sampling for Combinatorial Optimization (2506.03672v1)

Abstract: Combinatorial Optimization problems are widespread in domains such as logistics, manufacturing, and drug discovery, yet their NP-hard nature makes them computationally challenging. Recent Neural Combinatorial Optimization methods leverage deep learning to learn solution strategies, trained via Supervised or Reinforcement Learning (RL). While promising, these approaches often rely on task-specific augmentations, perform poorly on out-of-distribution instances, and lack robust inference mechanisms. Moreover, existing latent space models either require labeled data or rely on pre-trained policies. In this work, we propose LGS-Net, a novel latent space model that conditions on problem instances, and introduce an efficient inference method, Latent Guided Sampling (LGS), based on Markov Chain Monte Carlo and Stochastic Approximation. We show that the iterations of our method form a time-inhomogeneous Markov Chain and provide rigorous theoretical convergence guarantees. Empirical results on benchmark routing tasks show that our method achieves state-of-the-art performance among RL-based approaches.

• The paper presents LGS-Net, a latent-variable neural model that integrates continuous instance-conditioned latent spaces with guided MCMC sampling for combinatorial optimization.
• It employs time-inhomogeneous MCMC and stochastic approximation to enhance exploration, sample efficiency, and robust inference on TSP and CVRP benchmarks.
• Empirical results show near-zero and negative optimality gaps with improved out-of-distribution performance, setting new benchmarks for RL-based optimization methods.

Latent Guided Sampling for Combinatorial Optimization: Model, Theory, and Empirical Analysis

Overview and Motivation

This paper presents LGS-Net, a latent-variable neural model for combinatorial optimization (CO) that advances both modeling and inference methodology within Neural Combinatorial Optimization (NCO). The model integrates a continuous, instance-conditioned latent space and a guided inference procedure—Latent Guided Sampling (LGS)—based on time-inhomogeneous Markov Chain Monte Carlo (MCMC) and Stochastic Approximation (SA). The work addresses key limitations in prior NCO literature: 1) reliance on labeled data or pre-trained policies; 2) poor generalization to out-of-distribution instances; and 3) inference mechanisms deficient in exploration and sample efficiency. Rigorous convergence guarantees support the proposed inference algorithm, and experimental results on standard benchmarks for TSP and CVRP demonstrate decisively superior performance among RL-based methods.

Model Architecture

LGS-Net models the solution process as conditional sampling from a latent-variable generative model:

$$p_{\theta, \phi}(y | x) = \int p_{\phi}(z | x) \ p_{\theta}(y | x, z) \ dz$$

where $x$ represents the problem instance, $z$ is a latent variable drawn from the instance-conditioned encoder $p_{\phi}(z|x)$, and $y$ is the discrete solution generated sequentially via the decoder $p_{\theta}(y|x, z)$. Both encoder and decoder are parameterized with neural networks, the encoder following a multi-layer attention scheme with instance normalization and skip connections.

The decoder emits probabilities for feasible next actions in the partial solution, masking infeasible options as dictated by hard constraints (e.g., vehicle capacities in CVRP). The context at each step consists of the latent representation along with embeddings and problem-specific dynamic features.

Figure 1: Solution representations for TSP and CVRP produced by LGS-Net, visualizing the sequential nature and constraint handling in the decoder.

Training Procedure

Model training employs a loss intertwining cost minimization with entropy regularization to promote solution diversity:

$$\mathcal{L}(\theta, \phi; x) = \sum_{k=1}^{K} \mathbb{E}_{z^{k} \sim p_{\phi}(\cdot | x)} \left[ \mathbb{E}_{y^{k} \sim p_{\theta}(\cdot | x, z^{k})} \left[ w^{k} C(y^{k}, x) \right] + \beta \mathcal{H}(p_{\theta}(\cdot | x, z^{k})) \right]$$

where samples are weighted with an exponentially decayed temperature $\tau$ for cost normalization. Gradients are efficiently estimated using the reparameterization trick for latent variables, and the Adam optimizer is employed for parameter updates.

Inference: Latent Guided Sampling (LGS)

Given trained encoder and decoder, inference is formulated as sampling solutions from a reweighted distribution favoring low-cost assignments:

$$\pi_{\theta}(y | x) \propto \int p_{\phi}(z | x) p_{\theta}(y | z, x) e^{-\lambda C(y, x)} \, dz$$

Since direct sampling is intractable, LGS orchestrates multiple interacting MCMC chains over the latent space, guiding exploration with acceptance probabilities tied to both encoder likelihoods and cost improvements. Importantly, decoder parameters are adaptively updated via SA during inference using policy gradients computed on sampled solutions and latent variables:

$$H_{\theta}\left(x, \{\left(z^k, y^k\right)\}_{k=1}^{K}\right) = \frac{1}{K} \sum_{k=1}^{K} \left( C(y^k, x) - b(x) \right) \nabla_{\theta} \log p_{\theta}(y^k | x, z^k)$$

The method leverages parallel particle propagation and intermittent parameter adaptation to trade off exploration and exploitation effectively.

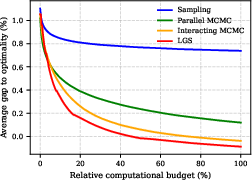
Figure 2: Comparative performance of inference methods on CVRP, highlighting superiority of LGS and interacting MCMC over classical and single-chain approaches.

(Figure 3)

Figure 3: Sampling-based inference performance over multiple runs, underscoring stability and improvement from interacting chains.

Theoretical Guarantees

The paper rigorously proves that the full sequence of $(z, y)$ pairs produced by LGS constitutes a time-inhomogeneous Markov chain converging geometrically to the target distribution. For fixed decoder parameters, explicit minorization and drift conditions yield geometric ergodicity in both total variation and $\mathrm{L}_2$ norm. When parameters are adapted via SA, the convergence theorem establishes an explicit bound comprising mixing error, tracking error, and optimization error. Notably, the method avoids assumptions of convexity or coercivity, enabling application to non-convex, discrete CO objectives encountered in practice.

Empirical Results

LGS-Net is evaluated on standard benchmarks for TSP and CVRP with both in-distribution and challenging out-of-distribution problem sizes. Tables report the cost, gap to optimality, and computation time. LGS-Net establishes new best results for RL-based methods, outperforming POMO, CVAE-Opt, EAS, COMPASS, and industrial solvers (LKH3, OR-Tools) in nearly all settings. Notable empirical findings include:

• Without domain-specific augmentation, LGS-Net achieves near-zero optimality gap on TSP and negative gap (improving upon the best known) on CVRP for $n=100,125$.
• Performance is robust out-of-distribution up to $n=150$, with competing augmentation-based methods only matching or barely improving for large instances under relaxed computational budgets.
• LGS is decisively superior to differential evolution and CMA-ES as inference procedures for latent-based NCO models, demonstrating the importance of guided MCMC and SA steps.

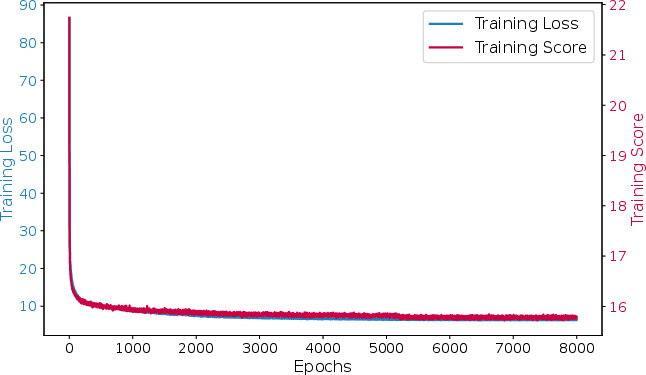
  Figure 4: Training dynamics: loss and score convergence for CVRP with $n=100$.

  

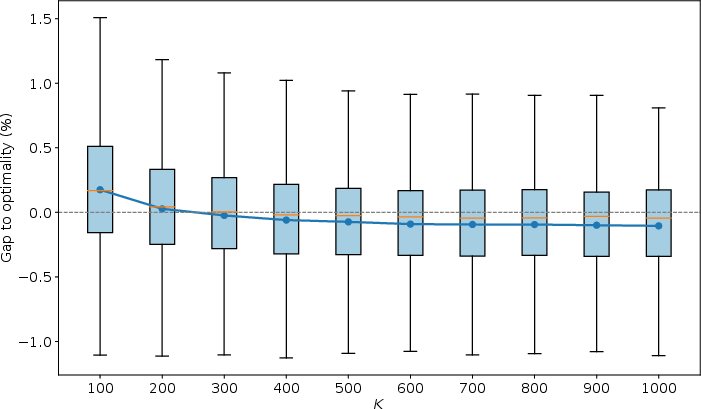
  Figure 5: Analysis of the effect of latent sample count $K$ on solution gap, indicating diminishing returns beyond moderate $K$.

  

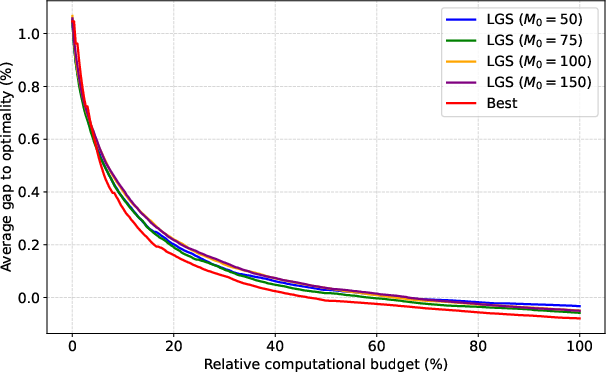
  Figure 6: Evaluation of SA update frequency strategies, showing improvements from adaptive schedules over fixed intervals.

Implementation Trade-offs and Practical Considerations

• Computational cost: LGS requires parallel MCMC chains and batch evaluations, but substantial efficiency can be obtained via hardware acceleration and judicious scheduling of SA updates.
• Sample efficiency: Propagation and adaptation of latent particles allow broader exploration, mitigating premature convergence to local minima typical in single-chain or naive stochastic sampling.
• Parameter adaptation: Empirical results suggest that adaptive, interval-based updates outperform constant-frequency adaptation.
• Scalability: Performance degrades gracefully with instance size, controlled by particle count and computational budget.

Implications and Future Directions

LGS-Net signifies a substantial advance in NCO methodology. Conditioning the latent space on problem instances and formulating inference as guided sampling with theoretical guarantees resolves prior issues with solution diversity and generalization. The approach facilitates deployment to previously inaccessible CO problems where labeled data and pre-trained policies are impractical, and out-of-distribution robustness is critical.

Practical extensions include automating adaptive schedules for parameter update intervals, integrating more sophisticated or problem-specific proposal mechanisms, and investigating the scaling properties on even larger, industrial-sized CO instances. The theoretical analysis may inform future research on mixing and convergence in other non-convex or hybrid discrete-continuous optimization domains, as well as latency-sensitive RL deployments.

Conclusion

LGS-Net sets a new benchmark for latent-variable NCO models, combining a principled model architecture with an inference algorithm holding strong theoretical and empirical credentials. The paper suggests that active adaptation and instance-conditioned latent exploration will continue to shape the evolution of neural methods for combinatorial optimization tasks, with broad implications for logistics, scheduling, and analogous discrete decision problems.