Weight-Space Linear Recurrent Neural Networks (2506.01153v1)

Abstract: We introduce WARP (Weight-space Adaptive Recurrent Prediction), a simple yet powerful framework that unifies weight-space learning with linear recurrence to redefine sequence modeling. Unlike conventional recurrent neural networks (RNNs) which collapse temporal dynamics into fixed-dimensional hidden states, WARP explicitly parametrizes the hidden state as the weights of a distinct root neural network. This formulation promotes higher-resolution memory, gradient-free adaptation at test-time, and seamless integration of domain-specific physical priors. Empirical validation shows that WARP matches or surpasses state-of-the-art baselines on diverse classification tasks, spanning synthetic benchmarks to real-world datasets. Furthermore, extensive experiments across sequential image completion, dynamical system reconstruction, and multivariate time series forecasting demonstrate its expressiveness and generalization capabilities. Critically, WARP's weight trajectories offer valuable insights into the model's inner workings. Ablation studies confirm the architectural necessity of key components, solidifying weight-space linear RNNs as a transformative paradigm for adaptive machine intelligence.

• The paper introduces WARP, a novel approach that parameterizes an RNN's hidden state as the weights of a root network for enhanced sequence modeling.
• The paper demonstrates that WARP achieves competitive performance with gradient-free adaptation and the integration of domain-specific priors across tasks like image completion, energy forecasting, and dynamical reconstruction.
• The paper’s ablation studies confirm the critical role of the root network and suggest that low-rank approximations could mitigate scaling challenges in large network implementations.

Weight-Space Linear Recurrent Neural Networks: A Novel Approach to Sequence Modeling

This paper introduces Weight-space Adaptive Recurrent Prediction (WARP), a novel framework that integrates weight-space learning with linear recurrence for sequence modeling. WARP redefines the hidden state of an RNN by explicitly parameterizing it as the weights of a distinct root neural network. This approach allows for higher-resolution memory, gradient-free adaptation during testing, and the integration of domain-specific physical priors.

Core Concepts and Architecture

Traditional RNNs compress temporal dynamics into fixed-dimensional hidden states, whereas WARP utilizes the weights of a separate root neural network as the hidden state. The core of WARP is the recurrence relation:

$\theta_t = A\theta_{t-1} + B\Delta \mathbf{x}_t$

where $\theta_t \in \mathbb{R}^{D_\theta}$ represents the weights of the root neural network at time step $t$, and $$\Delta \mathbf{x}_t = \mathbf{x}_t - \mathbf{x}_{t-1}$$ is the input difference. $A \in \mathbb{R}^{D_\theta \times D_\theta}$ is the state transition matrix, and $B \in \mathbb{R}^{D_\theta \times D_x}$ the input transition matrix. The output is computed as:

$\mathbf{y}_t = \theta_t(\tau)$

where $\tau = t/(T-1)$ is the normalized training time. The root network $\theta_t (\cdot)$ acts as a non-linear decoding function. WARP's architecture allows it to leverage both linear recurrence's efficiency and the expressiveness derived from the non-linearities within the root network.

Training and Inference

WARP supports both convolutional and recurrent training modes. In recurrent mode, the paper distinguishes between auto-regressive (AR) and non-AR settings. The AR setting is suited for noisy forecasting tasks and uses teacher forcing with scheduled sampling to mitigate exposure bias. During inference on regression problems, the model operates fully auto-regressively. The model minimizes either the mean-squared error (MSE) or the simplified negative log-likelihood (NLL) for probabilistic predictions. For classification, categorical cross-entropy is used.

Empirical Validation

The paper evaluates WARP across various tasks, including image completion, dynamical system reconstruction, and multivariate time series forecasting. Specifically, WARP was tested on:

• MNIST, Fashion MNIST, and CelebA for image completion
• ETT datasets for energy prediction
• MSD, Lotka-Volterra, and SINE for dynamical system reconstruction
• UEA datasets for time series classification

WARP matches or surpasses state-of-the-art baselines on these diverse classification tasks and demonstrates strong expressiveness and generalization capabilities in sequential image completion, dynamical system reconstruction, and multivariate time series forecasting. The authors highlight WARP's ability to achieve strong performance even in out-of-distribution scenarios.

Ablation Studies and Analysis

The authors perform ablation studies to validate the architectural necessity of key components. For instance, they find that eliminating the root network leads to a catastrophic degradation in model expressivity (Figure 1). They also show the importance of the diagonal decoding direction $\theta_t (\tau)$, illustrated for the MSD problem in Figure 2. Furthermore, experiments validate the importance of the initial hypernetwork $\phi: \mathbf{x}_0 \mapsto \theta_0$.

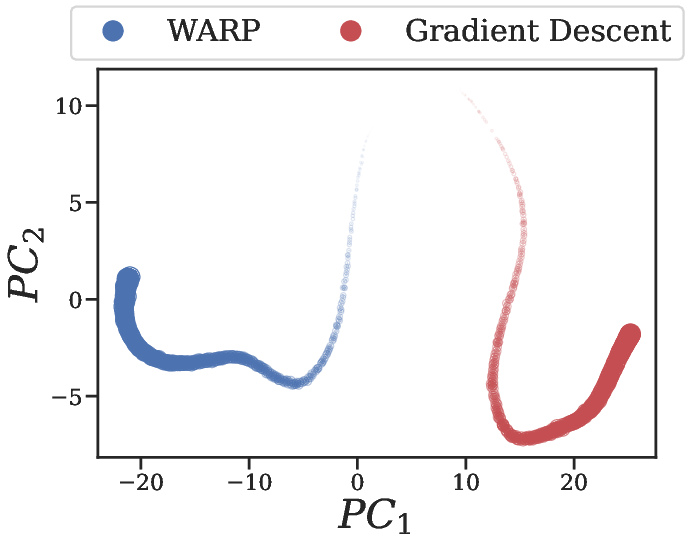
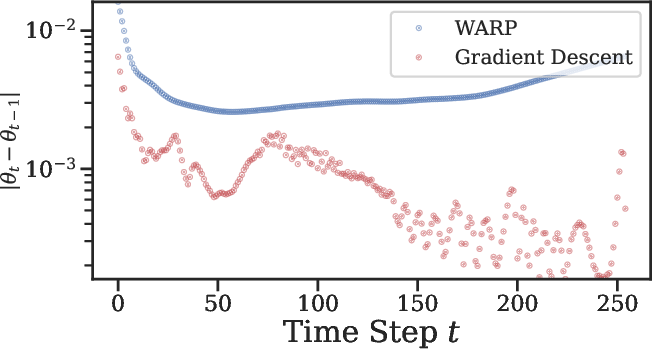
Figure 3: (a) Principal components of the weight-space of WARP vs. weight trajectory fitted via the Gradient Descent strategy on a single trajectory; (b) Norm of the difference between updates as we go through the time steps for WARP, and the gradient steps for Gradient Descent.

Advantages of WARP

The paper emphasizes several benefits of WARP, including gradient-free adaptation, seamless integration of domain-specific knowledge, and neuromorphic qualities. WARP's ability to fine-tune its weights without gradients via its data interaction (Figure 3) allows for test-time adaptation. Additionally, physics-informed strategies can be integrated.

Limitations and Future Directions

The authors acknowledge limitations, such as scaling to larger root networks due to the quadratic memory cost of the state transition matrix $A$. The paper suggests exploring low-rank or diagonal parameterizations to reduce the memory footprint. The authors also acknowledge the limited theoretical understanding of weight-space learning and suggest future work could expand the framework to cover other forms of analyses like time series imputation or control.

Conclusion

The paper presents WARP as a novel approach to sequence modeling that leverages weight-space learning and linear recurrence. WARP offers a unique parameterization of the RNN hidden state, leading to competitive performance, gradient-free adaptation, and the potential for integrating domain-specific knowledge. The experiments demonstrate WARP's potential as a transformative paradigm for adaptive machine intelligence.