Long Expressive Memory for Sequence Modeling (2110.04744v2)

Abstract: We propose a novel method called Long Expressive Memory (LEM) for learning long-term sequential dependencies. LEM is gradient-based, it can efficiently process sequential tasks with very long-term dependencies, and it is sufficiently expressive to be able to learn complicated input-output maps. To derive LEM, we consider a system of multiscale ordinary differential equations, as well as a suitable time-discretization of this system. For LEM, we derive rigorous bounds to show the mitigation of the exploding and vanishing gradients problem, a well-known challenge for gradient-based recurrent sequential learning methods. We also prove that LEM can approximate a large class of dynamical systems to high accuracy. Our empirical results, ranging from image and time-series classification through dynamical systems prediction to speech recognition and LLMing, demonstrate that LEM outperforms state-of-the-art recurrent neural networks, gated recurrent units, and long short-term memory models.

• The paper introduces a novel gradient-based method called Long Expressive Memory (LEM) that uses multiscale ODEs to address long-term dependencies.
• It employs implicit-explicit time discretization and gating functions to mitigate exploding/vanishing gradients while preserving expressivity.
• LEM demonstrates superior or comparable performance to LSTM and other RNN variants on various tasks including sequential image recognition and language modeling.

Long Expressive Memory for Sequence Modeling

The paper "Long Expressive Memory for Sequence Modeling" (2110.04744) introduces a novel gradient-based method named Long Expressive Memory (LEM) for addressing long-term dependencies in sequential data. LEM is designed to mitigate the exploding and vanishing gradients problem, a common challenge in training recurrent neural networks (RNNs), while maintaining sufficient expressivity to learn complex input-output mappings. The approach is grounded in a multiscale system of ordinary differential equations (ODEs) and its suitable time-discretization.

LEM Architecture and Motivation

The central idea behind LEM is the recognition that real-world sequential data often contains information at multiple time scales. The authors propose a multiscale ODE system as the foundation for LEM. This system consists of interconnected ODEs that capture both fast and slow dynamics within the sequential data. The simplest example of a two-scale ODE system is given by:

$$\frac{d}{dt}y(t) = \tau_y (\sigma(W_{yy}y(t) + W_{yz}z(t) + W_{yi}i(t) + b_y) - y(t)),$$

$$\frac{d}{dt}z(t) = \tau_z (\sigma(W_{zy}y(t) + W_{zz}z(t) + W_{zi}i(t) + b_z) - z(t)).$$

where $t \in [0,T]$ is continuous time, $0 < \tau_y \leq \tau_z \leq 1$ are time scales, $y(t) \in \mathbb{R}^{d_y}$ and $z(t) \in \mathbb{R}^{d_z}$ are slow and fast variables, and $i(t) \in \mathbb{R}^m$ is the input signal. The dynamic interactions are modulated by weight matrices and bias vectors, with a nonlinear tanh activation function $\sigma(u) = \tanh(u)$.

To generalize this to multiple scales, the authors propose:

$$\frac{d}{dt}y(t) = \hat{\sigma}(W_{1y}y(t) + W_{1z}z(t) + b_1) \odot (\sigma(W_{yy}y(t) + W_{yz}z(t) + W_{yi}i(t) + b_y) - y(t)),$$

$$\frac{d}{dt}z(t) = \hat{\sigma}(W_{2y}y(t) + W_{2z}z(t) + b_2) \odot (\sigma(W_{zy}y(t) + W_{zz}z(t) + W_{zi}i(t) + b_z) - z(t)).$$

Where $\hat{\sigma}(u) = 0.5(1+\tanh(u/2))$ is a sigmoid activation function and $\odot$ denotes element-wise multiplication. The terms $\hat{\sigma}$ can be interpreted as input and state-dependent gating functions, endowing the ODE with multiple time scales.

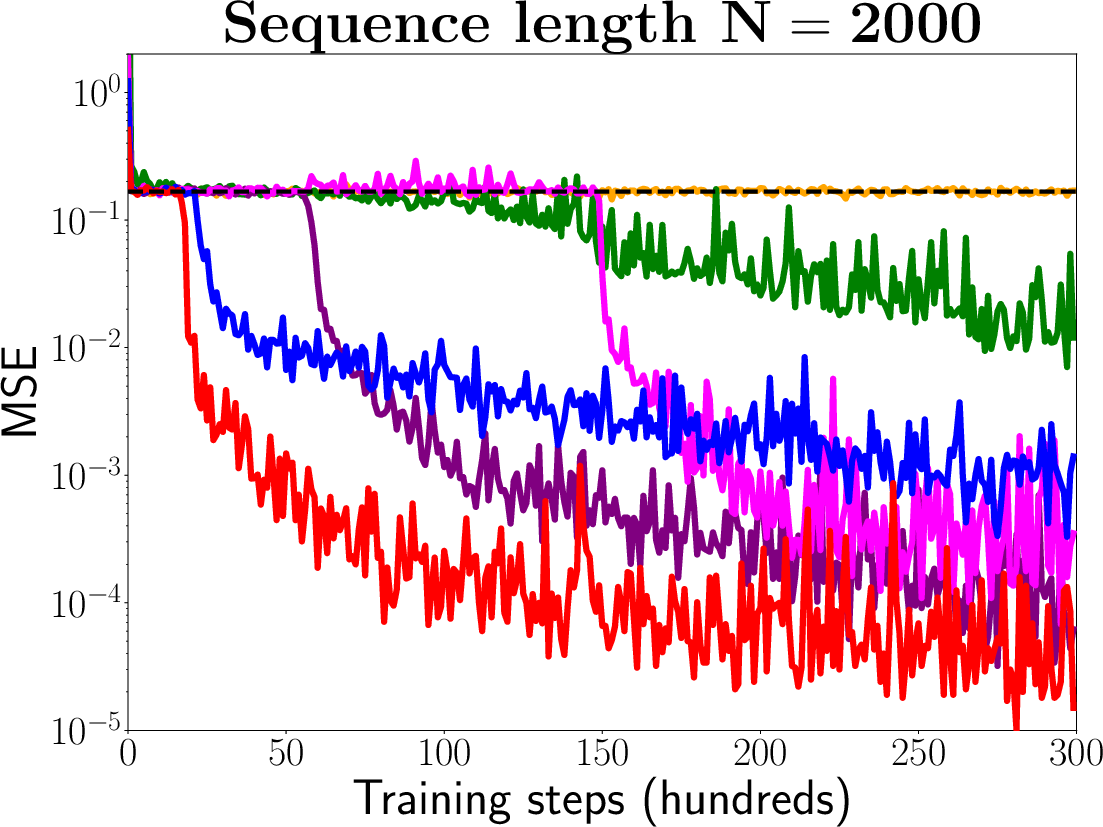
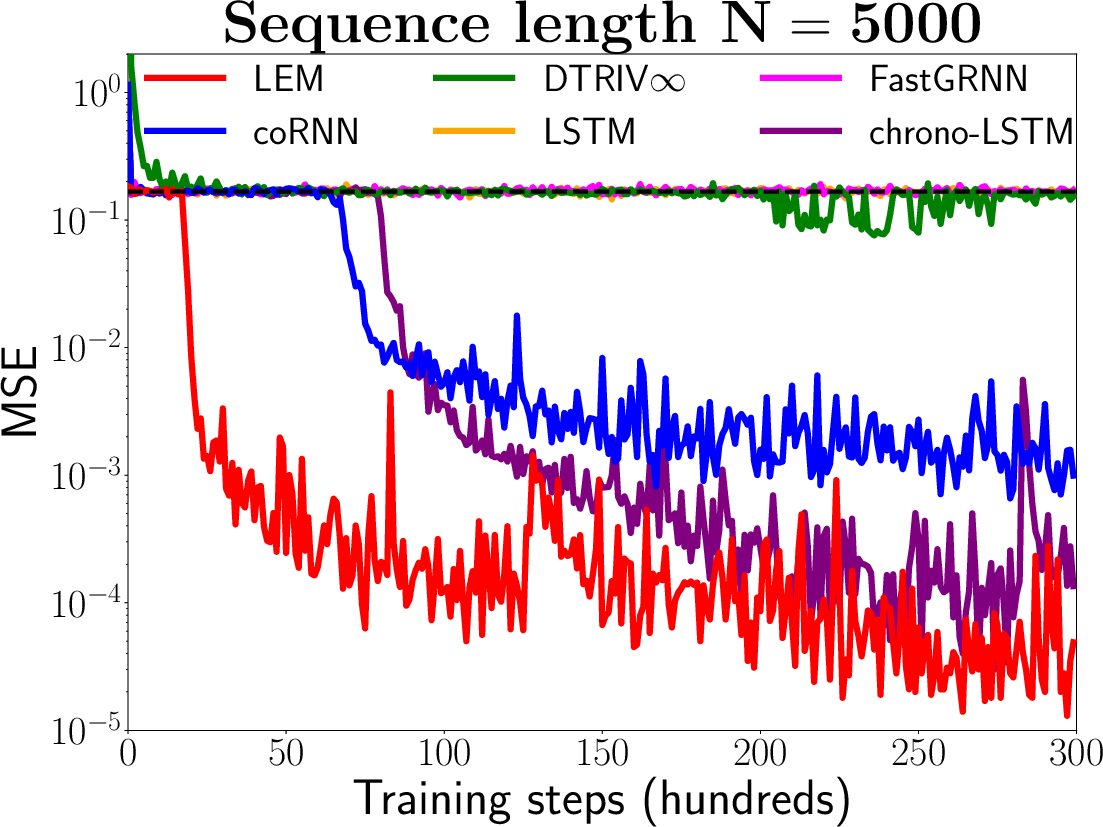
Figure 1: Results on the very long adding problem for LEM, coRNN, DTRIV$\infty$ [dtriv], FastGRNN [fastrnn], LSTM and LSTM with chrono initialization [warp] based on three very long sequence lengths $N$, i.e., $N=2000$, $N=5000$ and $N=10000$.

Time Discretization and LEM Formulation

To create a practical sequence model, the authors discretize the multiscale ODE system using an implicit-explicit (IMEX) time-stepping scheme. This discretization leads to the LEM architecture:

$$h_n = \hat{\sigma}(W_{1h}h_{n-1} + W_{1x}x_n + b_1),$$

$$c_n = \hat{\sigma}(W_{2h}h_{n-1} + W_{2x}x_n + b_2),$$

$$z_n = (1 - h_n) \odot z_{n-1} + h_n \odot \sigma(W_{zh}h_{n-1} + W_{zx}x_n + b_z),$$

$$y_n = (1 - c_n) \odot y_{n-1} + c_n \odot \sigma(W_{yh}h_{n} + W_{yx}x_n + b_y),$$

where $h_n, c_n \in \mathbb{R}^d$ are gating functions, $y_n, z_n \in \mathbb{R}^d$ are hidden states, and $x_n \in \mathbb{R}^m$ is the input state at step $n$. The matrices $W$ and vectors $b$ are learnable parameters. This formulation allows for adaptive learning of time scales, which is crucial for capturing long-term dependencies.

Rigorous Analysis

The paper presents a rigorous analysis of LEM, focusing on the exploding and vanishing gradients problem and the approximation capabilities of the model.

Bounds on Hidden States

The authors derive pointwise bounds on the hidden states of LEM, showing that they remain bounded during training. This is crucial for stability and preventing divergence.

Mitigation of Exploding and Vanishing Gradients

The analysis demonstrates that LEM mitigates the exploding and vanishing gradients problem. By deriving bounds on the gradients of the loss function with respect to the model parameters, the authors show that the gradients neither grow nor decay exponentially with sequence length. This allows LEM to effectively learn long-term dependencies.

Universal Approximation Theorems

The paper proves that LEM can approximate a large class of dynamical systems to arbitrary accuracy. This includes both general dynamical systems and multiscale dynamical systems. These theoretical results highlight the expressivity of LEM and its ability to learn complex input-output maps.

Empirical Evaluation

The authors conduct an extensive empirical evaluation of LEM on a variety of datasets, including:

• Very long adding problem: This synthetic task tests the ability of models to learn long-term dependencies.
• Sequential image recognition (sMNIST, psMNIST, nCIFAR-10): These tasks evaluate the performance of LEM on image classification with sequential input.
• EigenWorms: This dataset consists of very long sequences for genomics classification.
• Heart-rate prediction: This healthcare application involves predicting heart rate from PPG data.
• FitzHugh-Nagumo system prediction: This task involves predicting the dynamics of a two-scale fast-slow dynamical system.
• Google12 keyword spotting: This dataset is a widely used benchmark for keyword spotting.
• LLMing (Penn Tree Bank corpus): This task tests the expressivity of recurrent models on character-level and word-level LLMing.

The empirical results demonstrate that LEM outperforms or is comparable to state-of-the-art RNNs, GRUs, and LSTMs on each task. In particular, LEM shows strong performance on tasks with long-term dependencies and those requiring high expressivity.

Comparison to LSTM

The paper draws a detailed comparison between LEM and the widely used LSTM architecture. While LEM has the same number of parameters as an LSTM for the same number of hidden units, the experimental results indicate that LEM outperforms LSTMs on both expressive tasks and tasks involving long-term dependencies. The authors attribute this to the gradient stability and multiscale resolution capabilities of LEM.

Discussion and Conclusion

The paper concludes by highlighting the key advantages of LEM for sequence modeling. The combination of gradient-stable dynamics, specific model structure, and multiscale resolution enables LEM to learn long-term dependencies while maintaining sufficient expressivity for efficiently solving realistic learning tasks. The robustness of LEM's performance across various sequence lengths makes it a promising architecture for a wide range of sequential data applications.