Towards Interpretability Without Sacrifice: Faithful Dense Layer Decomposition with Mixture of Decoders (2505.21364v1)

Abstract: Multilayer perceptrons (MLPs) are an integral part of LLMs, yet their dense representations render them difficult to understand, edit, and steer. Recent methods learn interpretable approximations via neuron-level sparsity, yet fail to faithfully reconstruct the original mapping--significantly increasing model's next-token cross-entropy loss. In this paper, we advocate for moving to layer-level sparsity to overcome the accuracy trade-off in sparse layer approximation. Under this paradigm, we introduce Mixture of Decoders (MxDs). MxDs generalize MLPs and Gated Linear Units, expanding pre-trained dense layers into tens of thousands of specialized sublayers. Through a flexible form of tensor factorization, each sparsely activating MxD sublayer implements a linear transformation with full-rank weights--preserving the original decoders' expressive capacity even under heavy sparsity. Experimentally, we show that MxDs significantly outperform state-of-the-art methods (e.g., Transcoders) on the sparsity-accuracy frontier in LLMs with up to 3B parameters. Further evaluations on sparse probing and feature steering demonstrate that MxDs learn similarly specialized features of natural language--opening up a promising new avenue for designing interpretable yet faithful decompositions. Our code is included at: https://github.com/james-oldfield/MxD/.

• The paper presents MxDs, which decompose dense layers using a mixture of linear decoders and tensor factorization to achieve faithful model approximations.
• By employing layer-level sparsity, MxDs overcome the accuracy drop seen with neuron-level methods, preserving full-rank representations of original decoders.
• Experimental results on multiple LLMs show that MxDs reduce reconstruction loss while enabling interpretable feature steering and probing.

Faithful Dense Layer Decomposition with Mixture of Decoders

This paper introduces Mixture of Decoders (MxDs), a novel approach to decomposing dense layers in LLMs to enhance interpretability without sacrificing performance (2505.21364). MxDs address the limitations of existing methods that rely on neuron-level sparsity, which often leads to a significant increase in model cross-entropy loss due to poor reconstruction of the original mapping. By moving to layer-level sparsity, MxDs aim to overcome this accuracy trade-off and provide a more faithful representation of the original dense layers.

Addressing the Accuracy-Sparsity Trade-Off

The paper argues that preserving the base models' performance is crucial for sparse MLP layer approximations for model faithfulness and practical adoption. The MxDs framework employs a flexible tensor factorization to expand pre-trained dense layers into thousands of specialized sublayers, each implementing a linear transformation with full-rank weights. This design enables faithful reconstruction even under heavy sparsity, addressing the limitations of neuron-level sparsity methods like Transcoders [dunefsky2024transcoders]. The central claim is that MxDs outperform state-of-the-art methods on the sparsity-accuracy frontier in LLMs with up to 3B parameters, while also maintaining competitive interpretability through sparse probing and feature steering.

Figure 1: Units of specialization for sparse layer variants: Neuron-level sparsity of existing sparse MLPs dunefsky2024transcoders, paulo2025transcoders vs layer-level sparsity (right), which the proposed Mixture of Decoders (MxD) layer enables at scale.

Mixture of Decoders: Methodology

The MxD layer approximates the original MLP with a conditional combination of $N$ linear transformations, expressed as:

$$\mathrm{MxD}(\mathbf{x}) = \sum_{n=1}^N a_n (\mathbf{W}_n^\top \mathbf{z})$$

where $\mathbf{a}$ are sparse expert coefficients from a learnable gating matrix $\mathbf{G}$, and $\mathbf{z}$ is the dense output from an encoder. A key aspect of MxDs is the parameterization of the third-order weight tensor $\boldsymbol{\mathcal{W}\in\mathbb{R}^{N\times H \times O}$ to yield full-rank expert weights through a Hadamard product factorization:

$$\boldsymbol{\mathcal{W}(n,h,:) = \mathbf{c}_n * \mathbf{d}_h \in \mathbb{R}^{O}, \qquad \forall\,n\!\in\{1,\ldots,N\},\; h\!\in\{1,\ldots,H\}}$$

This factorization reduces the parameter count while preserving the expressive capacity of each expert sublayer. The paper includes a lemma proving that each specialized MxD expert's weights inherit the same rank as the original MLP's decoder, ensuring faithful approximation even in very sparse models.

Rank Preservation and Forward Pass

The preservation of rank in MxD expert weights is a key theoretical contribution. The paper proves that under mild conditions, each expert's weight matrix inherits the rank of the original MLP's decoder matrix. This allows MxDs to retain layer capacity even under high sparsity, unlike sparse MLPs whose hidden units are confined to a $K$-dimensional subspace, limiting their ability to faithfully approximate the original mapping. Additionally, the paper presents a lemma demonstrating a factorized forward pass for MxDs, which simplifies implementation and reduces computational cost.

Experimental Validation

The experimental section demonstrates MxDs' superior performance on the accuracy-sparsity frontier across four LLMs: GPT2-124M, Pythia-410m, Pythia-1.4b, and Llama-3.2-3B. By training sparse layers to minimize the normalized reconstruction loss between the original MLP output and the MxD output, the results show that MxDs not only outperform Transcoders but also preserve model performance at various sparsity levels. The paper also evaluates the interpretability of MxD features through sparse probing and feature steering experiments. Probing results show that individual MxD expert units are predictive of various categories of news articles, while steering experiments demonstrate that MxD features contribute mechanistically to the LLM's forward pass in a predictable way.

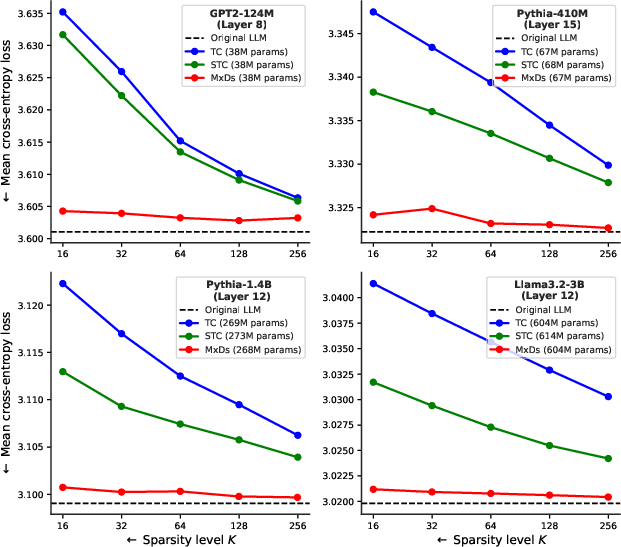
Figure 2: Model cross-entropy loss preserved when replacing MLPs with Transcoders [dunefsky2024transcoders], Skip Transcoders [paulo2025transcoders], and MxDs, as a function of the number of active units $K$ (hidden neurons/experts).

Connections to Existing Literature

The paper situates MxDs within the broader context of sparse decompositions and conditional computation. It connects MxDs to sparse autoencoders (SAEs) and other methods for learning sparse, non-negative features in neural networks. It also discusses the relationship between MxDs and Mixture of Experts (MoE) architectures, highlighting the parameter efficiency and scalability of MxDs compared to traditional MoEs. The paper further notes the connection to conditional adapters, showing that MxDs generalize prior adapter-based MoEs as a special case.

Conclusion

The paper concludes by emphasizing the benefits of decomposing dense layers' computations into a mixture of interpretable sublayers. The MxD layer achieves this at scale, preserving the matrix rank properties of the original decoders and outperforming existing techniques on the sparsity-accuracy frontier. The paper acknowledges limitations, including the computational cost of the large encoders and gating function in MxDs and the potential for expert imbalance. Future work could explore hierarchical structures and efficient retrieval mechanisms for further reductions in FLOPs. Overall, the paper makes a strong case for layer-level sparsity as an important step towards interpretability without sacrificing model performance. The claim that specialization doesn't have to come with a high cost to model performance is backed by significant numerical improvements. This suggests a promising new direction for designing interpretable and efficient LLMs.