Exploring Self-Organized Criticality through Memory-Driven Random Walks on Complex Networks (2505.19296v1)

Abstract: We present a stochastic model of memory-driven random walks on complex networks, where a single walker explores the network through a combination of local random walks and memory-based resetting. The walker either moves to a neighboring node or resets to a previously visited node with a probability proportional to the visitation history.Each node in the network accumulates stress with every visit, and once the accumulated stress exceeds a threshold, the node topples, redistributing the stress to its neighbors. This redistribution can trigger cascading avalanches across the network. We demonstrate that this simple memory-driven mechanism, combined with local stress dynamics, leads to the emergence of self-organized criticality (SOC) across various network topologies, including Small-World and BA networks.The resulting avalanche size distributions follow power-law statistics, with exponents that are consistent with those found in classical SOC systems. Our model requires no fine-tuning of parameters to achieve criticality and offers a novel insight into how memory, network structure, and local stress interactions can give rise to emergent critical phenomena. These findings have implications for understanding cascading failures in infrastructure, neural avalanches in brain dynamics, and information spread in complex networks.

• The paper introduces a novel memory-driven random walk model that induces self-organized criticality without the need for parameter tuning.
• It demonstrates how combining local exploration with memory resets triggers cascading avalanches and power-law distributions across different network topologies.
• Results indicate that increased memory strength amplifies avalanche sizes and critical behavior, offering insights into network resilience.

Exploring Self-Organized Criticality through Memory-Driven Random Walks on Complex Networks

This paper presents a stochastic model for understanding self-organized criticality (SOC) via memory-driven random walks on complex networks. The model employs a unique combination of local random walks and memory-based resetting, leading to SOC without parametric tuning, across various network topologies such as Small-World and Barabási–Albert networks.

Introduction

The study explores non-Markovian random walks, contrasting them with traditional random walks that assume no memory. Real-world systems, such as human mobility, often exhibit memory, influencing movement dynamics. The paper builds on the work of Guerrero-Estrada et al., which explores memory-driven dynamics resulting in SOC in networks by invoking preferential memory dynamics. Here, a walker on a network accumulates stress at nodes, triggering toppling events akin to the sandpile model, ultimately resulting in cascading avalanches of varying sizes conforming to power-law distributions.

Figure 1: Heatmap of node visit frequencies for different memory strengths $q$ and 1600 nodes, averaged over 10 runs on a small-world network. High memory (larger $q$) leads to more concentrated visitation.

Model Dynamics

Walker Dynamics

A single walker navigates the network through a combination of local exploration and memory resets. The walker, at time $t$, can either randomly move to an adjacent node with probability $(1-q)$ or reset to a previously visited node based on a memory-driven probability proportional to past visits, controlled by the strength parameter $q$.

Stress Accumulation and Avalanching

Nodes accumulate stress with each visit. Once a node's stress surpasses its threshold $T$, it topples, redistributing stress to neighbors, potential cascading into an avalanche of topplings.

Figure 2: Illustration of a single avalanche event on a Watts-Strogatz small-world network with 400 nodes, where each node is connected to 4 neighbors and rewiring probability is 0.1. The memory strength ($q$) is set to 0.1. Nodes are colored based on the number of times they toppled during the cascade.

Results and Network Analysis

Small-World Networks

In small-world networks, characterized by their local clustering and short path lengths, the model demonstrates SOC through power-law avalanche distributions. The introduction of memory amplifies stress accumulation, producing larger avalanches as $q$ increases, with scaling behavior evident in larger networks.

Figure 3: Stress dynamics over time for three sample nodes (Node 50, Node 100, and Node 150). The plot shows how stress levels fluctuate over time, with sharp drops indicating toppling events.

Barabási–Albert Networks

In scale-free Barabási–Albert networks, large avalanches dominate due to the hub-dominated structure. The finite-size scaling of these networks shows the system's convergence towards a critical state with increasing network size. The hub-driven dynamics ensure frequent returns to high-degree nodes, fostering SOC without external tuning.

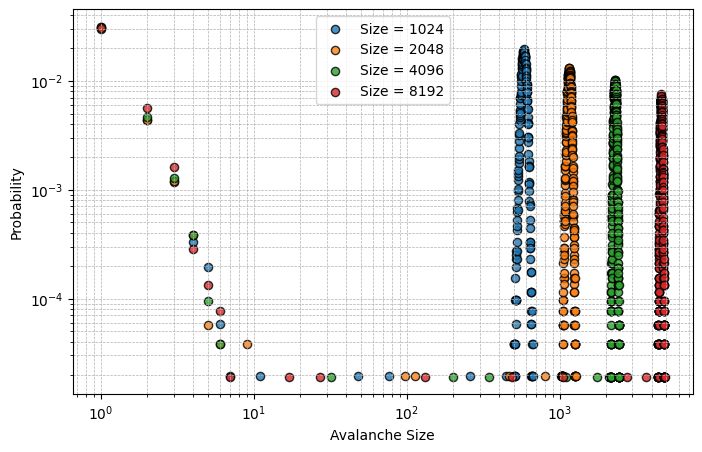
Figure 4: Avalanche size distribution for Barabási–Albert network of different sizes: $N = 256$, $512$, $1024$, and $2048$, $q = 0.2$. Large avalanches dominate due to hub-driven dynamics.

Discussion

The model integrates memory and stress redistribution to achieve SOC across diverse networks without parameter finetuning. The increasing memory strength $q$ enhances the avalanche size, reflecting the supercritical behavior. The findings emphasize memory's role in SOC, with varying network topologies influencing avalanche dynamics.

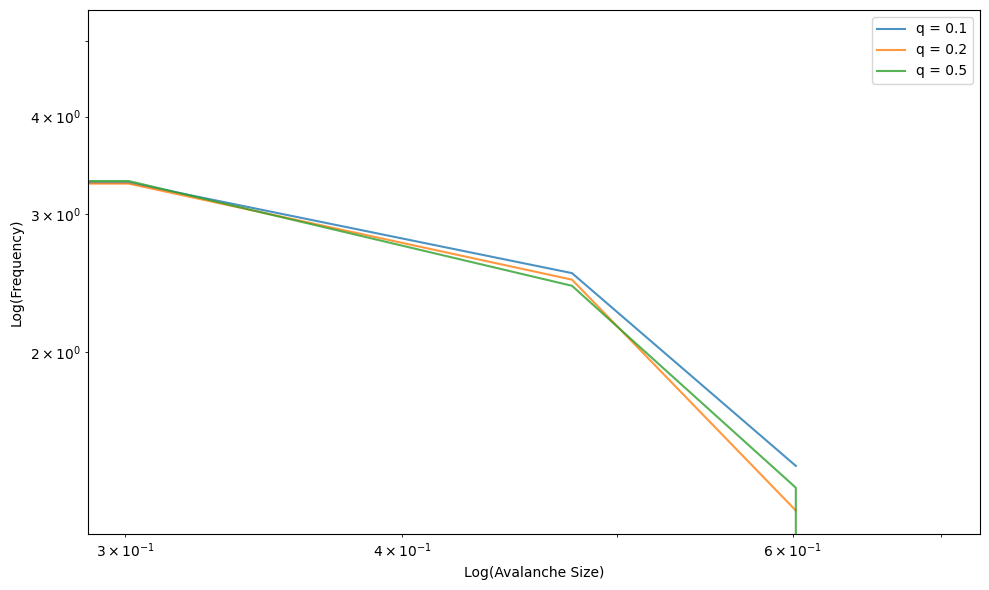
Figure 5: Avalanche size distribution for different memory strengths $q$. As $q$ increases, larger avalanches dominate due to increased memory feedback, showing a shift towards supercritical behavior.

Network Topology and Resilience

The study evaluates how varying the rewiring probability $p$ in small-world models impacts SOC dynamics. Moderate $p$ values achieve a synergy between local clustering and global randomness, optimal for SOC. Excessive randomness tends to diminish the SOC by disrupting the underlying network structure.

Figure 6: Avalanche size distribution for different rewiring probabilities $p$, averaged over 10 runs.

Conclusion

The study introduces a comprehensive framework combining memory and stress propagation to explore SOC in complex networks, revealing that memory-driven walks catalyze SOC without external adjustments. The model's robustness across different networks provides insight into managing cascades in systems ranging from neural networks to infrastructure networks. Future work could expand on these dynamics by integrating heterogeneous memory and further exploring the critical transitions in varying network structures.