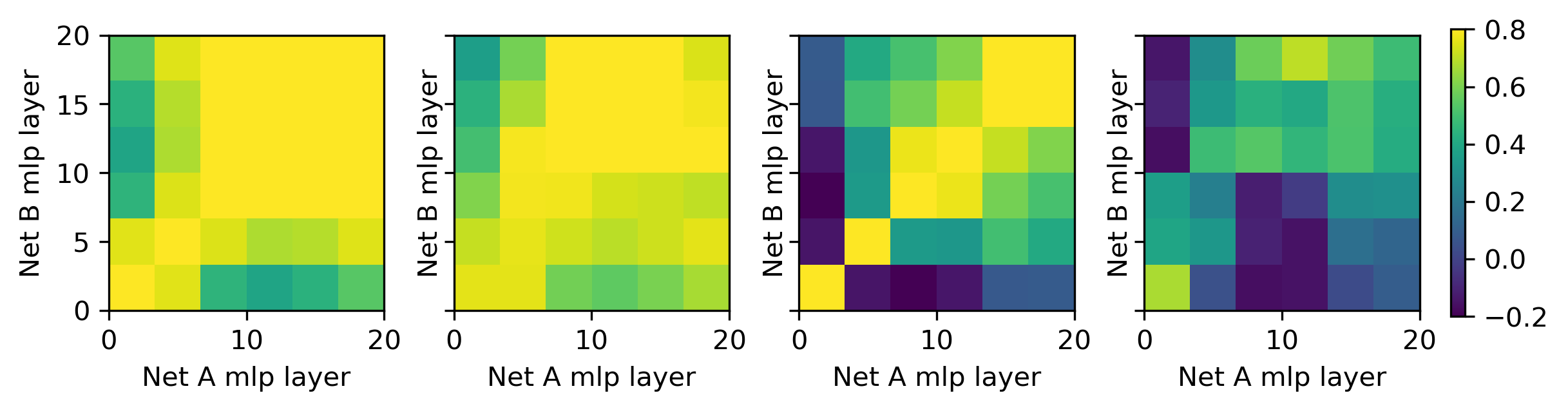Neural Thermodynamics I: Entropic Forces in Deep and Universal Representation Learning (2505.12387v1)

Abstract: With the rapid discovery of emergent phenomena in deep learning and LLMs, explaining and understanding their cause has become an urgent need. Here, we propose a rigorous entropic-force theory for understanding the learning dynamics of neural networks trained with stochastic gradient descent (SGD) and its variants. Building on the theory of parameter symmetries and an entropic loss landscape, we show that representation learning is crucially governed by emergent entropic forces arising from stochasticity and discrete-time updates. These forces systematically break continuous parameter symmetries and preserve discrete ones, leading to a series of gradient balance phenomena that resemble the equipartition property of thermal systems. These phenomena, in turn, (a) explain the universal alignment of neural representations between AI models and lead to a proof of the Platonic Representation Hypothesis, and (b) reconcile the seemingly contradictory observations of sharpness- and flatness-seeking behavior of deep learning optimization. Our theory and experiments demonstrate that a combination of entropic forces and symmetry breaking is key to understanding emergent phenomena in deep learning.

• The paper introduces an entropic loss function capturing SGD's stochasticity, revealing new dynamics in training and symmetry breaking.
• It demonstrates that entropic forces induce gradient balance and universal alignment across network layers, consistent with thermodynamic principles.
• The framework reconciles the edge of stability phenomenon with loss landscape evolution, offering insights for more effective deep learning strategies.

Neural Thermodynamics I: Entropic Forces in Deep and Universal Representation Learning

Introduction

The paper "Neural Thermodynamics I: Entropic Forces in Deep and Universal Representation Learning" presents a novel theoretical framework that applies entropic forces to understand the dynamics of neural networks trained using stochastic gradient descent (SGD) and its variants. The authors argue that the learning behaviors of modern neural networks are not only influenced by explicit optimization but also by implicit forces resulting from stochasticity and discretized updates, leading to phenomena akin to those observed in physical systems.

Entropic Loss Function

The paper introduces the concept of an entropic loss function, which incorporates an effective entropy term that accounts for the stochastic and discrete nature of SGD.

$$\phi_\eta := \ell + \eta \phi_1 + \eta^2 \phi_2 + O(\eta^3),$$

where $\ell$ is the original loss, and $\phi_\eta$ is the modified loss capturing entropic corrections. The entropic forces thus systematically break continuous parameter symmetries while preserving discrete ones.

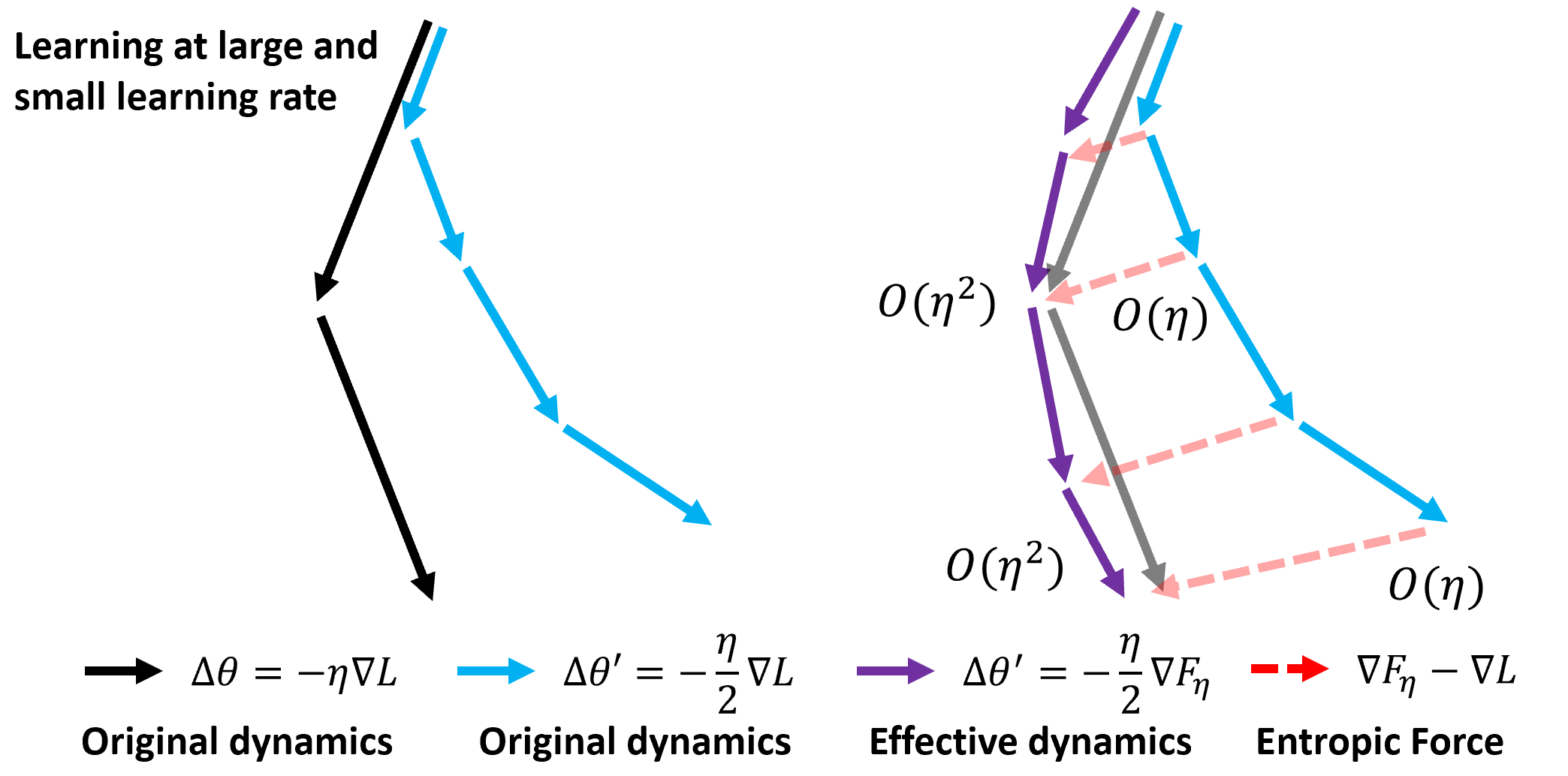
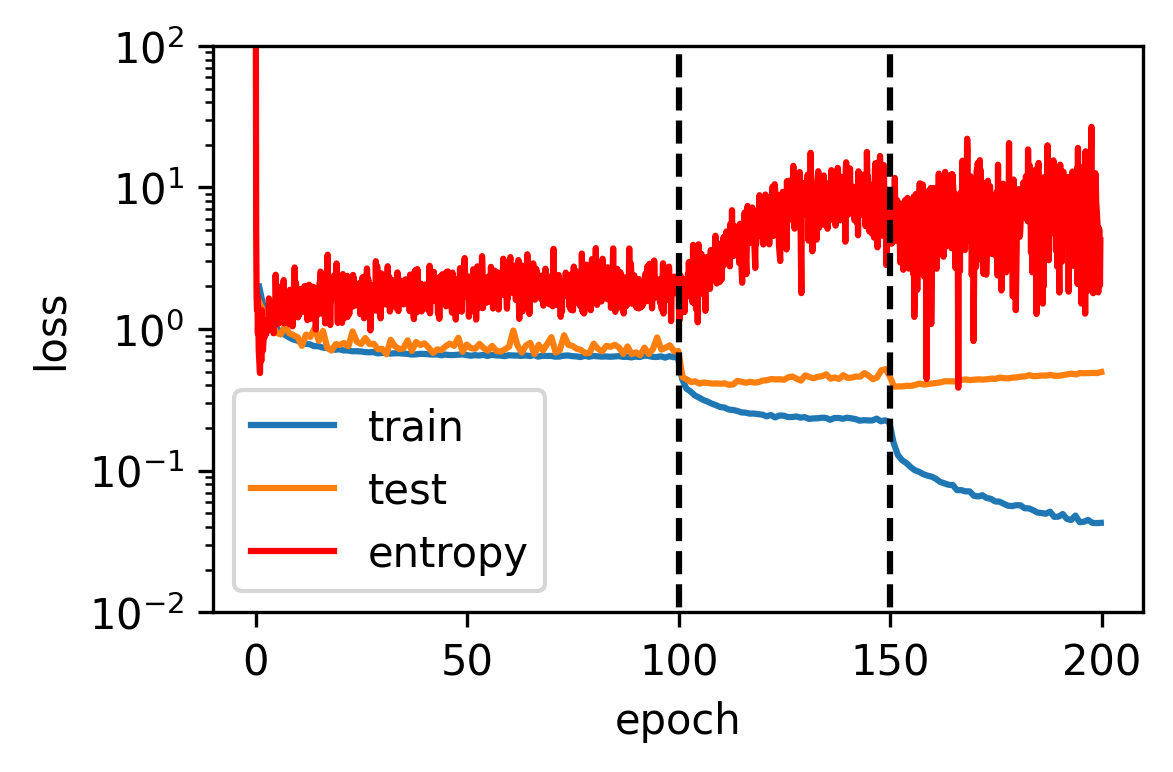
Figure 1: Entropic forces due to discretization error and stochasticity. The learning dynamics differ based on learning rate, showing entropy's role in the training process.

Gradient Balance and Symmetry Breaking

The paper demonstrates that entropic forces lead to gradient balance phenomena akin to the equipartition property in thermodynamics. The symmetry breaking caused by these forces explains why certain universal alignment behaviors are observed in deep learning, such as the Platonic Representation Hypothesis—a tendency for networks trained under different conditions to converge to similar internal representations.

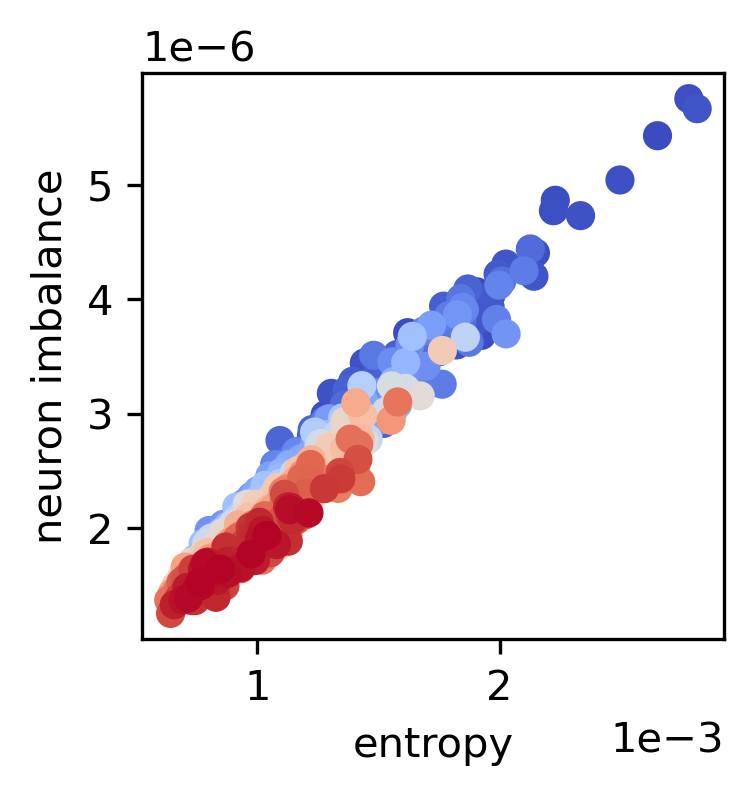
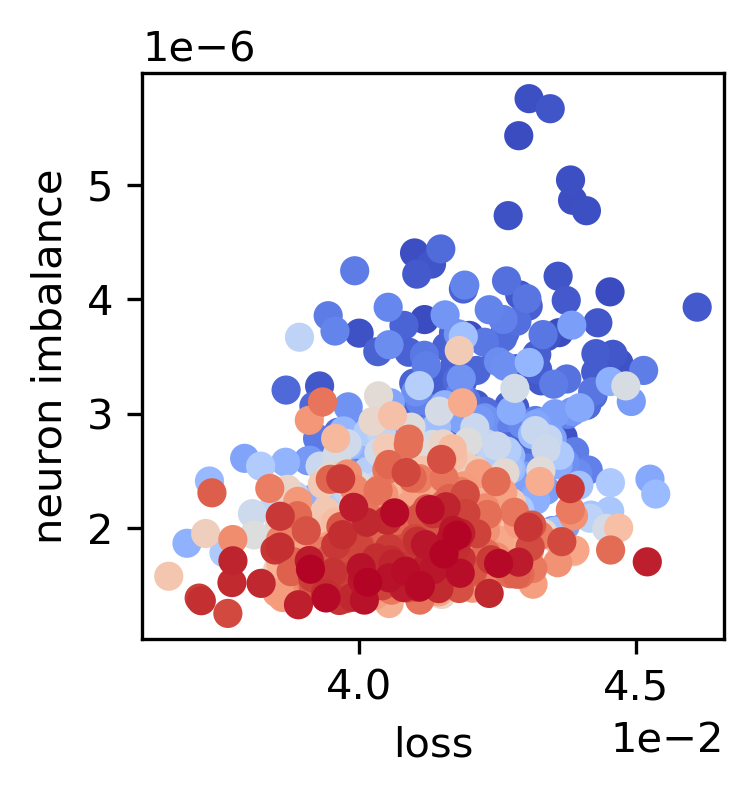
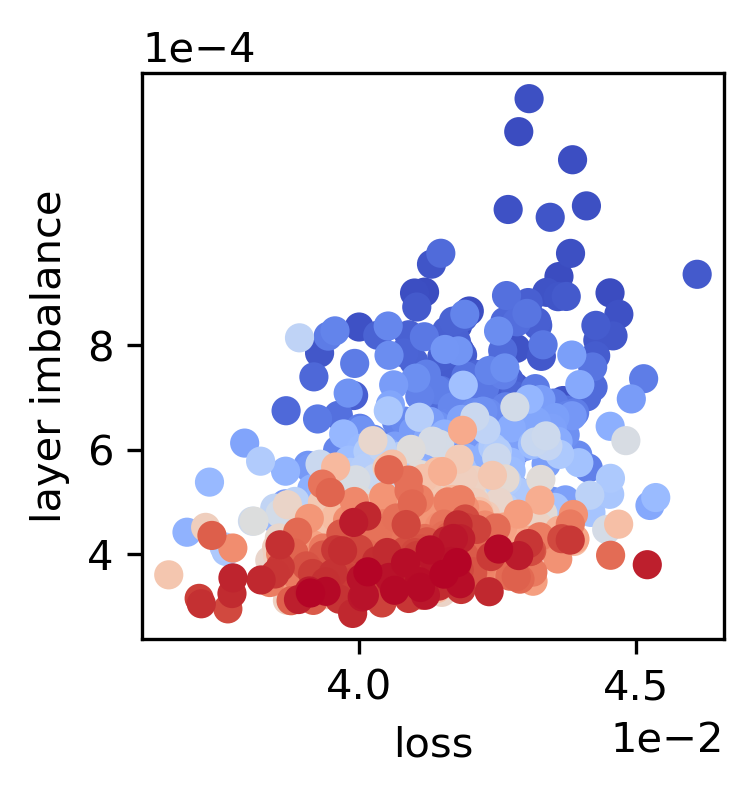
Figure 2: Layer and neuron gradient balance during training of a two-layer ReLU network, highlighting the correlation between entropy and balance.

Universal Representation and Alignment

The entropic framework provides a theoretical explanation for the observed alignment of neural representations across independently trained networks. At convergence, representations from different layers across networks can be aligned through an orthogonal transformation, supporting the hypothesis of universal representation learning.

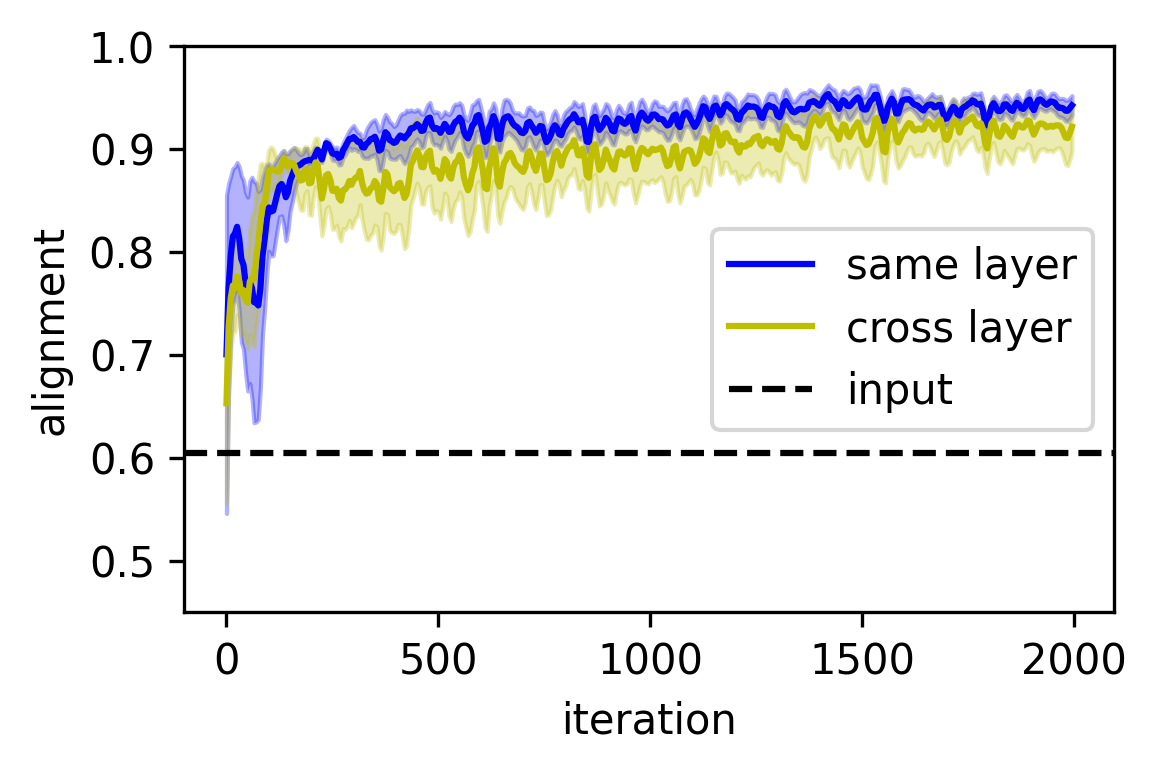
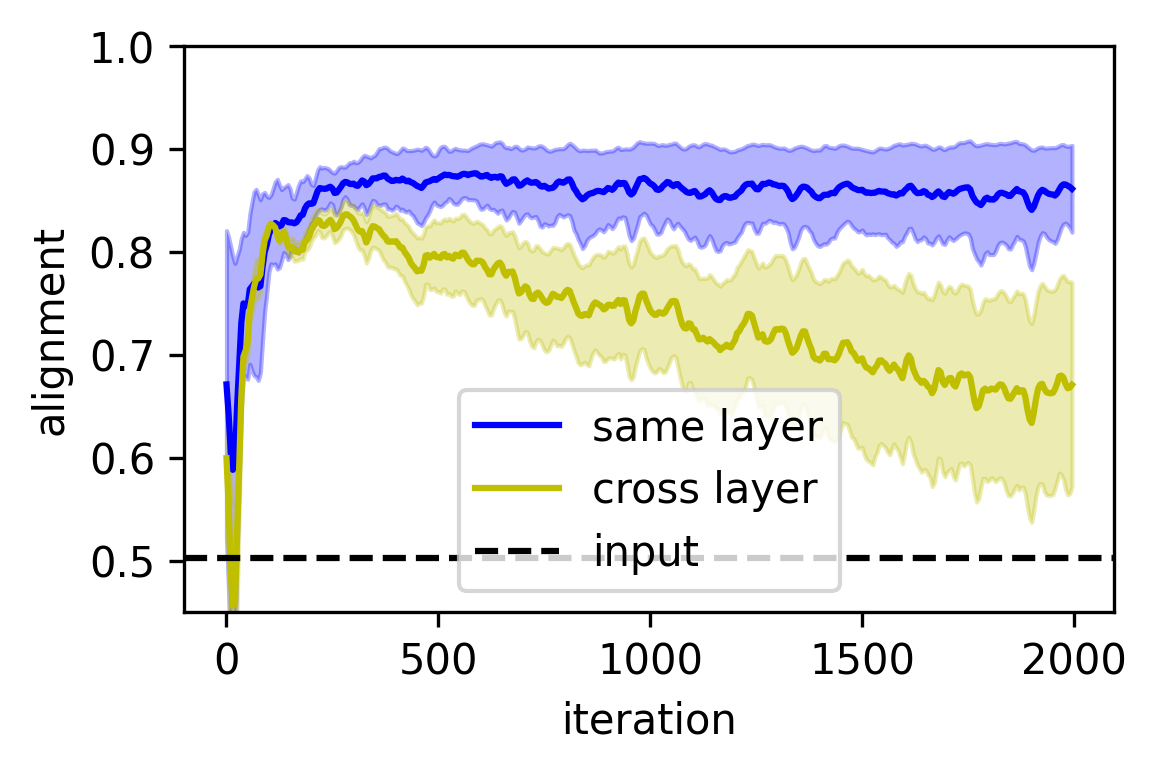
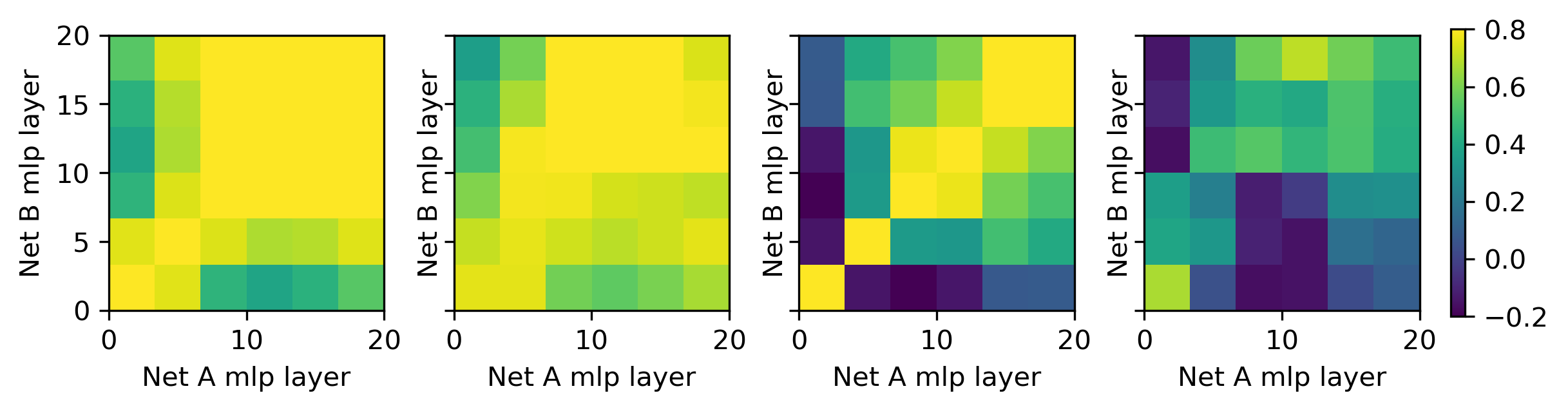
Figure 3: Representation alignment of two 6-layer networks trained on transformed data, showing persistent alignment across layers.

Entropic Forces and Stability

The paper discusses the implications of entropic forces on the edge of stability (EOS) phenomenon observed in deep learning. The framework predicts conditions under which training dynamics lead to either progressive sharpening or flattening of the loss landscape, reconciling seemingly contradictory behaviors of networks seeking both sharp and flat minima.

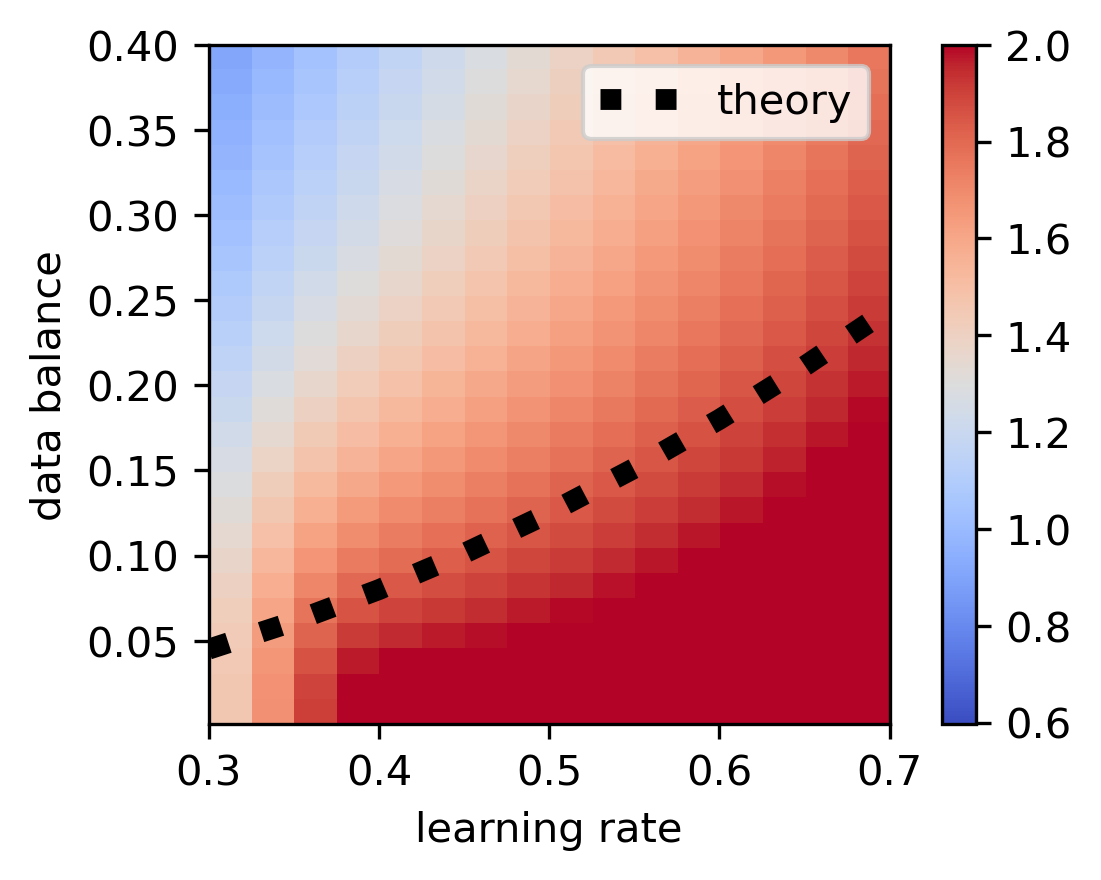
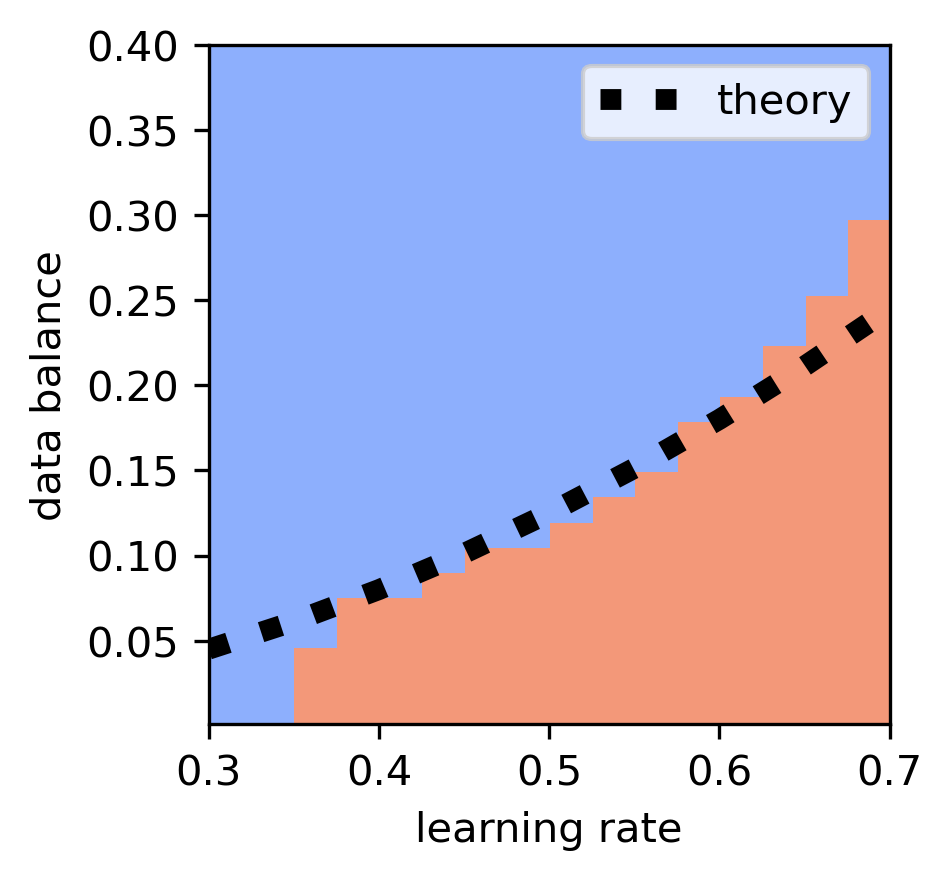
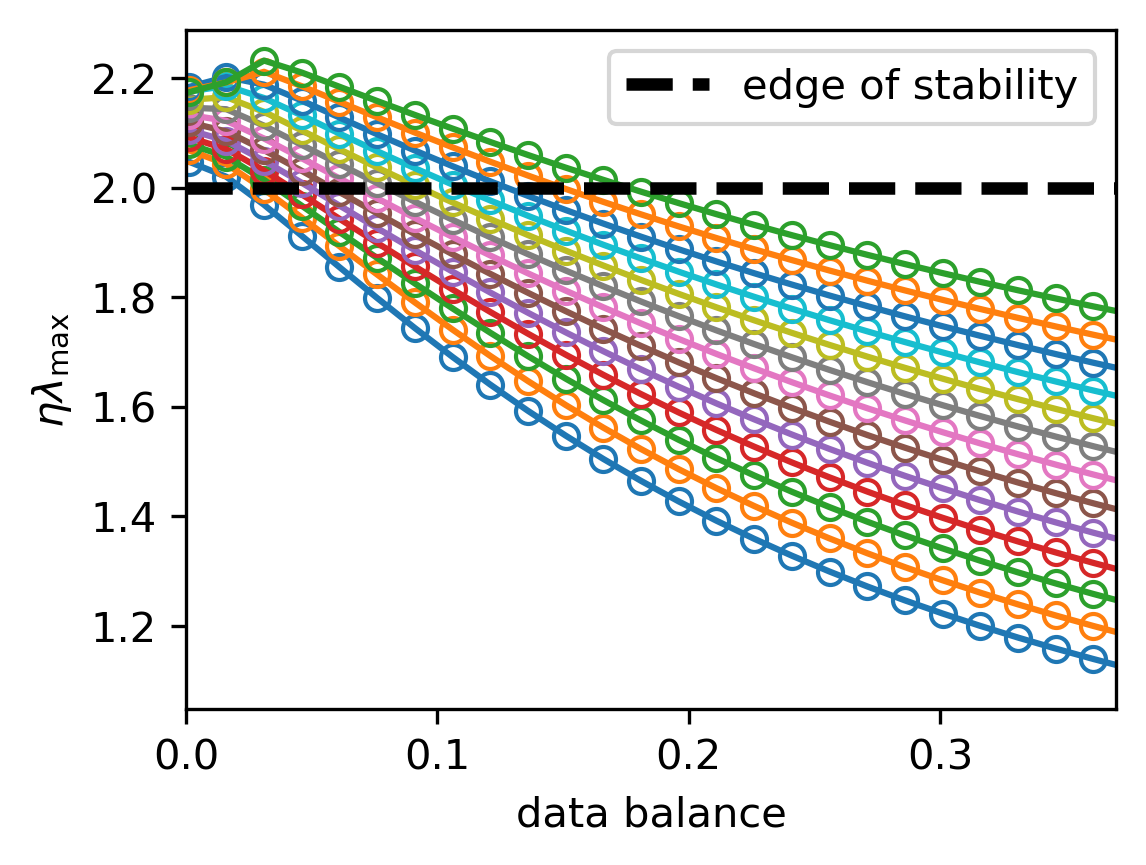
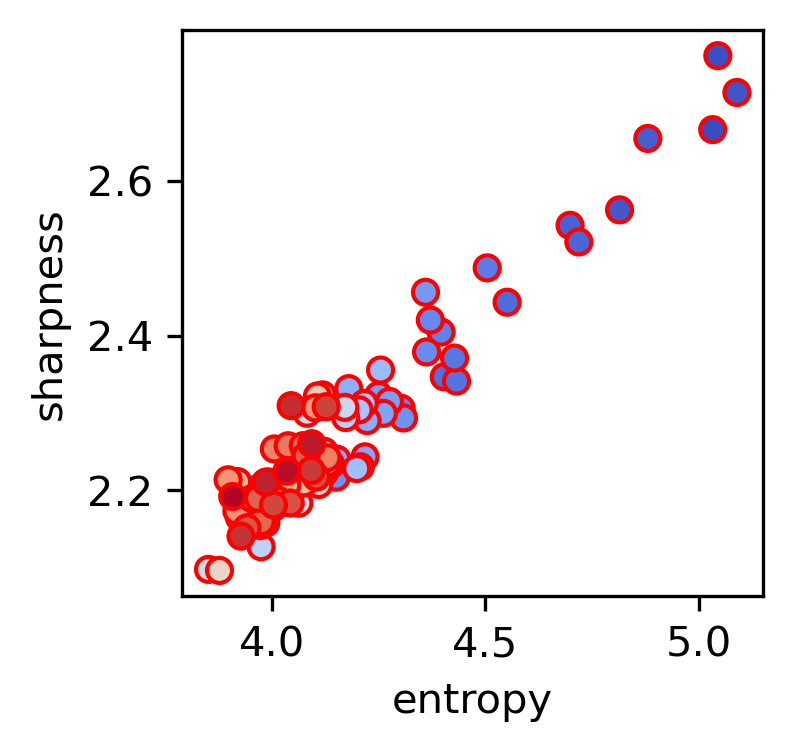
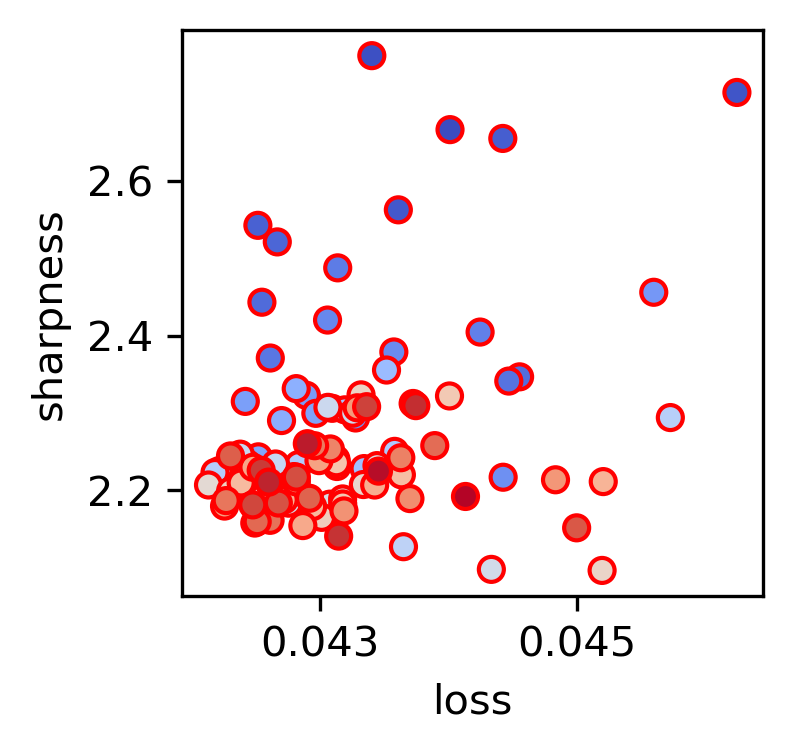
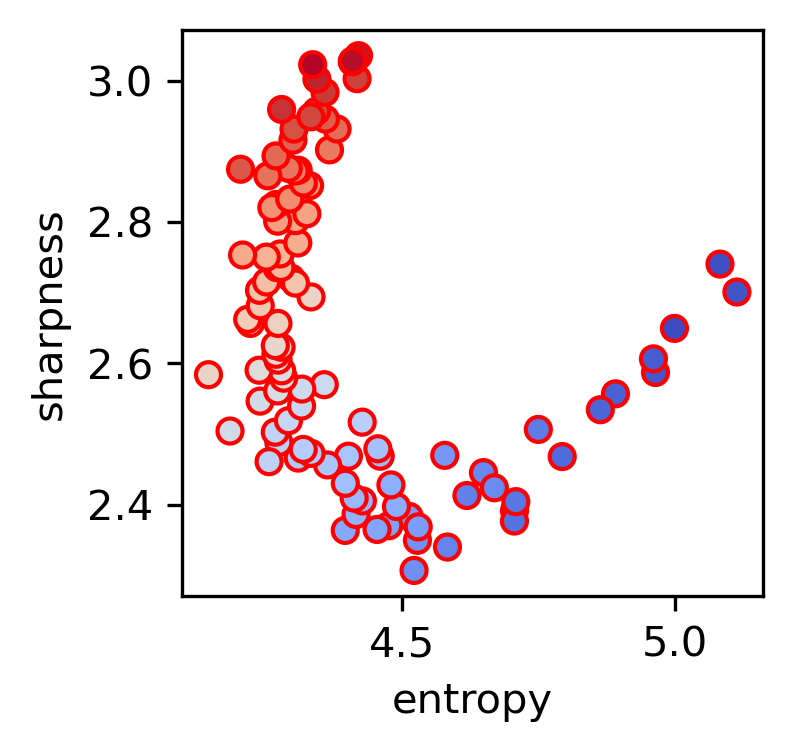
Figure 4: Entropic theory predicting the boundary for the edge of stability, illustrating how data balance affects solution sharpness.

Conclusion

The paper introduces a comprehensive entropic-force theory that not only explains emergent behaviors in neural networks but also suggests new avenues for research in the thermodynamics of deep learning. The approach unifies several disparate observations under a single framework, offering insights into the interplay between symmetry, entropy, and optimization dynamics in deep learning models. Future work will extend this framework, exploring its implications for non-equilibrium dynamics and the potential for phase transitions in neural networks.