Token-Level Uncertainty Estimation for Large Language Model Reasoning (2505.11737v1)

Abstract: While LLMs have demonstrated impressive capabilities, their output quality remains inconsistent across various application scenarios, making it difficult to identify trustworthy responses, especially in complex tasks requiring multi-step reasoning. In this paper, we propose a token-level uncertainty estimation framework to enable LLMs to self-assess and self-improve their generation quality in mathematical reasoning. Specifically, we introduce low-rank random weight perturbation to LLM decoding, generating predictive distributions that we use to estimate token-level uncertainties. We then aggregate these uncertainties to reflect semantic uncertainty of the generated sequences. Experiments on mathematical reasoning datasets of varying difficulty demonstrate that our token-level uncertainty metrics strongly correlate with answer correctness and model robustness. Additionally, we explore using uncertainty to directly enhance the model's reasoning performance through multiple generations and the particle filtering algorithm. Our approach consistently outperforms existing uncertainty estimation methods, establishing effective uncertainty estimation as a valuable tool for both evaluating and improving reasoning generation in LLMs.

• The paper introduces token-level uncertainty estimation using low-rank random weight perturbation to assess LLM reasoning quality.
• Results show strong correlations between aggregated token uncertainties and correctness, particularly in mathematical reasoning tasks.
• The framework, validated on benchmarks like GSM8K and MATH500, improves generation selection and guidance in LLMs.

Token-Level Uncertainty Estimation for LLM Reasoning

This essay summarizes "Token-Level Uncertainty Estimation for LLM Reasoning" (2505.11737), which introduces a method for estimating the uncertainty of LLM generations at the token level, with a focus on enhancing mathematical reasoning. The framework employs low-rank random weight perturbation to generate predictive distributions, which are then used to quantify token-level uncertainties. These uncertainties are aggregated to reflect the semantic uncertainty of generated sequences, demonstrating strong correlations with answer correctness and model robustness in mathematical reasoning tasks.

Introduction and Motivation

LLMs, despite their advancements, often struggle to reliably assess the quality of their own responses, particularly in complex reasoning scenarios. Existing uncertainty estimation methods typically focus on short-form question answering or require marginalization over the entire output space, making them intractable for long-form generation tasks. Addressing these limitations, this paper proposes a token-level uncertainty estimation framework to enable LLMs to self-assess and self-improve their generation quality in mathematical reasoning.

Methodology

The core of the proposed method involves introducing low-rank random weight perturbations to the LLM decoding process. This approach creates an ensemble of model variants without requiring costly retraining or extensive parameter updates. The total uncertainty of each generated token is decomposed into aleatoric uncertainty (inherent randomness in the data) and epistemic uncertainty (model uncertainty about its parameters). These token-level uncertainties are then aggregated to evaluate entire reasoning sequences.

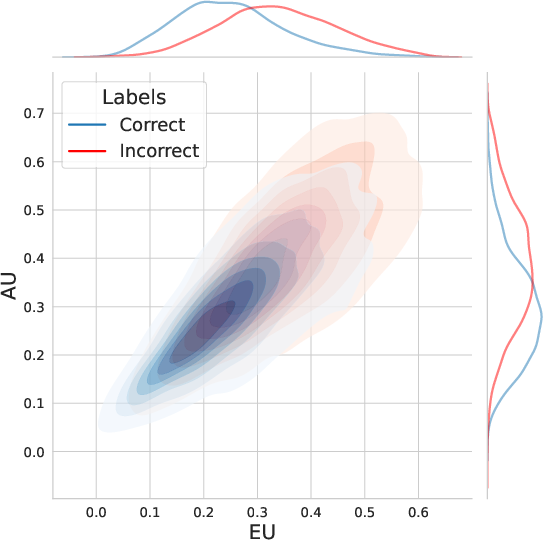
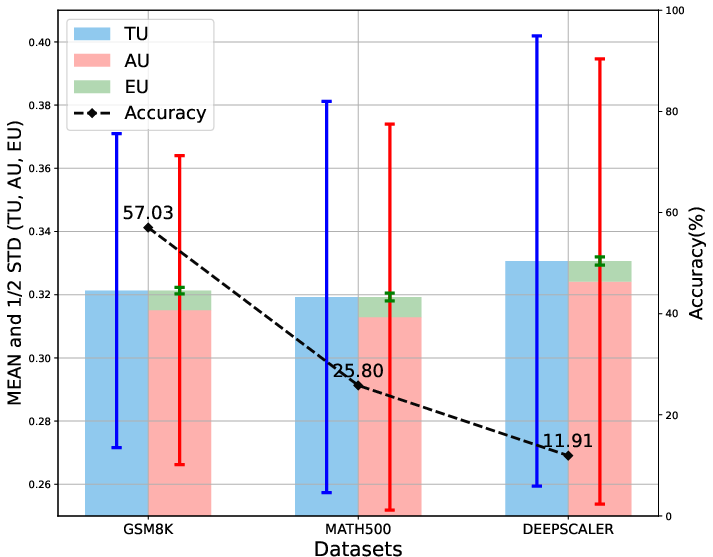
Figure 1: Distribution of responses from GSM8K [cobbe2021gsm8k] plotted in the EU-AU uncertainty space, as quantified by token-level uncertainty metrics.

Given an approximate posterior $q(\theta|\mathcal{D})$, a fixed input sequence $x \in \mathcal{X}$ and a specific output sequence $y=(y_1, y_2, \ldots, y_T) \in \mathcal{Y}$ sampled from the base policy $p(y|x)$, the predictive distribution of the next token $y_t$ produced by marginalization over weights is denoted as $$\bar{p}(y_t|y_{<t},x) \triangleq E_{\theta \sim q(\cdot|\mathcal{D})}[p(y_t|y_{<t},x;\theta)]$$. For the time step $t$, the following metrics are defined: \begin{itemize} \item Total Uncertainty (TU): $$\operatorname{TU}(y_t | y_{<t}, x) \triangleq H[\bar{p}(y_t|y_{<t},x)] = -\sum_{y_t\in\mathcal{V}}\bar{p}(y_t|y_{<t},x)\log \bar{p}(y_t|y_{<t},x)$$, \item Aleatoric Uncertainty (AU): $$\operatorname{AU}(y_t | y_{<t}, x) \triangleq E_{\theta \sim q(\cdot|\mathcal{D})}[H[p(y_t | y_{<t},x;\theta)]]$$, \item Epistemic Uncertainty (EU): $$\operatorname{EU}(y_t | y_{<t}, x) \triangleq \operatorname{TU}(y_t | y_{<t}, x) - \operatorname{AU}(y_t | y_{<t}, x) = \mathcal{I}(y_t ; \theta| y_{<t},x)$$. \end{itemize} The uncertainty of sequence $y$ is estimated by the length-normalized token-level uncertainty: $$\bar{\mathcal{U}}(y | x) = {1}{T}\sum\nolimits_{t=1}^T \mathcal{U}(y_t| y_{<t}, x)$$, where $\mathcal{U}$ denotes any of the uncertainty estimation methods (TU, AU, or EU).

Low-Rank Weight Perturbation

The method employs a low-rank structure of the noise added to the model weights. Given a rank-$r$ weight matrix $W_0 \in \mathbb{R}^{m \times n}$ of a neural network layer, a compact Singular Value Decomposition (SVD) is performed: $W_0 = U\Sigma V^\top$, where $\Sigma \succ 0 \in \mathbb{R}^{r \times 1}$ is the vector of singular values, and $U \in \mathbb{R}^{m \times r}$, $V \in \mathbb{R}^{n \times r}$ contain orthonormal columns. A low-rank noise matrix $\epsilon\in\mathbb{R}^{n\times r^{\prime}}$ is introduced, whose rank $r^\prime \ll r$ is significantly smaller than the rank of the weight matrix, and whose entries are sampled i.i.d. from a Gaussian distribution with standard deviation $\sigma_q$: $\epsilon_{ij} \sim \mathcal{N}(0, \sigma_q^2)$. The perturbed weight matrix is then constructed as $W = W_0 + V' \epsilon^\top$, where $V'$ is the matrix composed of the top-$r^\prime$ columns of $V$. This perturbation transforms the deterministic $W_0$ to a variational low-rank isotropic Gaussian distribution.

Experimental Results

The effectiveness of the proposed uncertainty modeling framework is demonstrated across three key aspects: (i) token-level epistemic uncertainty effectively identifies incorrect reasoning paths, outperforming baselines across three mathematical reasoning benchmarks; (ii) uncertainty metrics excel at selecting high-quality solutions from multiple candidates; and (iii) uncertainty functions as an implicit reward to guide reasoning, improving accuracy when combined with particle filtering for step-by-step generation. The experiments were conducted on three mathematical reasoning benchmarks of varying difficulty levels: GSM8K, MATH500, and DeepScaleR, using two open-source LLMs: Llama-3.2-1B-Instruct and Llama-3.1-8B-Instruct.

Analysis of Uncertainty Distribution and Dataset Difficulty

A preliminary paper examined the relationship between responses' token-level uncertainties and their correctness using the GSM8K dataset. The results showed that both epistemic and aleatoric uncertainties provide a better-than-chance separation between correct and incorrect outputs, indicating that the uncertainty estimates meaningfully correlate with generation quality. The paper also explored whether token-level uncertainties, when aggregated at the dataset level, can reflect the properties of the data. Datasets with higher difficulty tend to exhibit larger standard deviations in uncertainty, suggesting that as reasoning complexity increases, the model's uncertainty becomes more volatile.

Uncertainty in Detecting Incorrect Reasoning Paths

The paper treats uncertainty as a scoring function to identify incorrect responses for long-form reasoning tasks. The metrics used include AUROC, AUPRC, and Top-50\% ACC. Epistemic Uncertainty (EU) consistently outperforms all baseline methods in terms of AUROC, AUPRC, and Top-50\% Accuracy on nearly all datasets. For instance, with Llama-3.2-1B-Instruct on GSM8K, EU achieves 74.24\% AUROC and 77.31\% ACC*, significantly outperforming the P(True) baseline (55.97\% AUROC, 63.41% ACC*).

\subsection{Enhancing Generation Quality with Token-Level Uncertainties} The paper explores the direct application of uncertainty estimation of sequences to reasoning tasks to enhance the generation quality. Two strategies are evaluated: generation selection and generation guidance. For generation selection, EU is the most effective in selecting high-quality generations. Across the tested datasets, EU consistently outperforms the baseline Log-Likelihood (LL), demonstrating the potential of uncertainty estimation to enhance the downstream performance of LLMs. For generation guidance, uncertainty is used as an intrinsic reward, without relying on an explicit reward model. While the performance gain from uncertainty estimation is not significant, the experiment offers valuable insights that may inform the future design of process reward models.

Related Work

The paper contrasts its approach with existing methods, highlighting its novelty in estimating token-level uncertainties with rigorous theoretical foundations, representing a step toward extending Bayesian LLMs to long-form generation scenarios. It also discusses limitations of current uncertainty estimation techniques, such as reliance on log-probability or its variants.

Conclusion

This paper introduces a framework to quantify uncertainty in LLM reasoning generations by incorporating low-rank random weight perturbation during the LLM decoding procedure. The method connects with theoretically sound sequence-level uncertainty estimation methods and demonstrates that token-level epistemic uncertainty effectively identifies the quality of generated reasoning paths. Preliminary evidence supports the practical value of using uncertainty estimation to improve reasoning performance in LLMs.

Limitations

The approach has three key limitations: (i) computational overhead from multiple weight perturbation sampling runs; (ii) inability of token-level uncertainty aggregation to capture complex cross-token semantic inconsistencies; and (iii) high-variance problems in the theoretical connection between token and sequence uncertainties.