Separating balls with partly random hyperplanes with a view to partly random neural networks (2505.10470v1)

Abstract: We derive exact expressions for the probabilities that partly random hyperplanes separate two Euclidean balls. The probability that a fully random hyperplane separates two balls turns out to be significantly smaller than the corresponding probabilities for hyperplanes which are not fully random in certain cases. Our results motivate studying partially random neural networks and provide a first step in this direction.

• The paper introduces a methodology to calculate the probability of separating two Euclidean balls using partly randomized hyperplanes.
• It differentiates between scenarios with random biases, random weights, and fully random configurations via exact mathematical expressions.
• The findings offer insights for enhancing RVFL neural network architectures by leveraging selective randomization in high-dimensional classification.

Separating Balls with Partly Random Hyperplanes

This essay provides a comprehensive summary and analysis of the paper titled "Separating balls with partly random hyperplanes with a view to partly random neural networks". The paper presents a novel investigation into the probabilities of separating two Euclidean balls using partly random hyperplanes and extends the discussion to applications in neural networks, notably in architectures such as the Random Vector Functional Link (RVFL) network.

Introduction to Partially Random Hyperplanes

The paper explores the probability calculations that partly random hyperplanes will effectively separate two Euclidean balls. It emphasizes three scenarios: hyperplanes with deterministic weights and random biases, random weights and deterministic biases, and fully random configurations. The fundamental motivation is to determine efficiencies in neural network separations inspired by the random neural network architectures presented by Dirksen et al. in "The Separation Capacity of Random Neural Networks" (DeWolfe et al., 2023).

The central task in this context is evaluating the ability of different configurations of random and deterministic components in hyperplanes to achieve separation, a critical operation in classification tasks.

Mathematical Formulation

The focus is on evaluating the probability $$P(H[w;b] \text{ separates } B[c,r] \text{ and } B[x,p])$$, where $H[w;b]$ defines a hyperplane separating balls centered at $c$ and $x$ with radii $r$ and $p$, respectively. This leads to exact expressions deduced for different types of hyperplanes:

• Random Biases: The analysis shows that the probability of separation when only biases are random is influenced by the separation distance $\delta$ between the balls and is formulated as $\delta/(2k)$, where $k$ denotes the bias range.
• Random Weights: When weights are random, the probability is framed using the regularized beta function and shows a dependency on the geometric properties of the ball arrangements.
• Fully Random Configurations: Finally, the scenario where both weights and biases are random is extensively analyzed, demonstrating a combined effect that reduces the separating probability compared to when only one component is random.

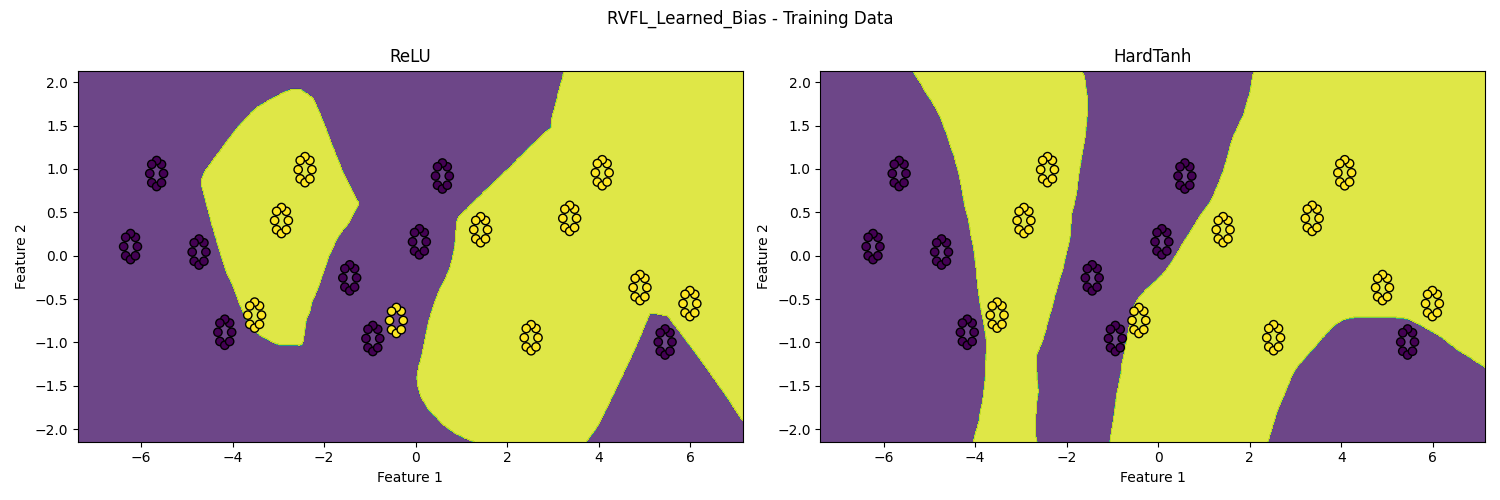
Figure 1: Binary classification decision boundaries for RVFL (top) and RVFL with learned biases (bottom) with ReLU (left) and hardtanh (right) activation functions. Figure courtesy of Guido Wagenvoorde, Mathematics Department, Utrecht University (master student).

Implications for Neural Networks

The implications of these findings extend to largely random neural network architectures. The RVFL network, which uses random weights and learned biases, exemplifies partially random networks in real-world applications. Such architectures align with the geometric insights derived about hyperplane orientations and separations.

Partially random networks, as demonstrated, hold a significant structural advantage in classification tasks, particularly in high-dimensional data scenarios where fully random component configurations may falter in achieving effective separation due to rapid dimensionality space expansion.

Discussion and Future Directions

The paper suggests that incorporating partly random layers in neural networks can offer a balance between efficiency and effectiveness. The theoretical results point towards potential improvements in neural network architectures, where certain layers might better benefit from randomization of particular components based on task-specific geometric considerations.

Further research is indicated, particularly numerical evaluations as initiated by Wagenvoorde, assessing the practical performance of these network configurations. Future extensions could also investigate hyperplane tessellations further and their relationship with network layer transformations, as highlighted by ongoing research in random hyperplane arrangements.

Conclusion

This detailed investigation into partly random hyperplanes provides a foundational step towards understanding and leveraging randomness within neural networks. By rigorously formulating and validating probabilities of separation with different configurations, the paper sets the stage for future explorations into enhanced neural network designs capable of efficient training and classification in complex task environments.