QCD$_2$ 't Hooft model: 2-flavour mesons spectrum (2504.12081v1)

Abstract: We continue analytical study of the meson mass spectrum in the large-$N_c$ two-dimensional QCD, known as the 't Hooft model, by addressing the most general case of quarks with unequal masses. Based on our previous work, we develop non-perturbative methods to compute spectral sums and systematically derive large-$n$ WKB expansion of the spectrum. Furthermore, we examine the behavior of these results in various asymptotic regimes, including the chiral, heavy quark, and heavy-light limits, and establish a precise coincidence with known analytical and numerical results obtained through alternative approaches.

• The paper advances analytic expansions of the 't Hooft model to determine the two-flavour meson spectrum for arbitrary quark mass asymmetry.
• It reformulates the original singular integral equation into a TQ finite-difference equation using Fourier transforms, ensuring precise spectral quantization.
• Extensive numerical validation confirms the analytic predictions across regimes from the chiral to heavy-light limits in 2D QCD.

Analytical Study of the Two-Flavour Meson Spectrum in the 't Hooft Model

Introduction

The paper "QCD$_2$ 't Hooft model: 2-flavour mesons spectrum" (2504.12081) investigates the analytic structure of the meson mass spectrum in two-dimensional quantum chromodynamics (QCD$_2$) in the planar (large-$N_c$) limit, focusing on the 't Hooft model with two quark flavours of unequal masses. It systematically generalizes techniques developed for the equal-mass case, extending non-perturbative and WKB-based analytic expansions for the spectrum to the arbitrary mass case and emphasizing the underlying integrability of the model. The authors provide explicit constructions for spectral sums, analyze various limiting regimes, and offer precise comparisons of analytical formulas with numerical calculations.

Reformulation of the 't Hooft Equation and the Integrable Structure

The core of the analysis is the re-expression of the 't Hooft equation as a difference (TQ) equation in Fourier space, valid for arbitrary quark mass parameters. This formulation leverages deeper connections to integrable systems due to its relation to Baxter's equation, enabling powerful analytic control over the spectrum.

A critical technical step is the Fourier transform with respect to the "rapidity-like" variable $\vartheta$, mapping the original singular integral eigenvalue problem into a homogeneous Fredholm equation with an integrable kernel. This in turn leads to a second-order finite-difference equation for the meromorphic $Q$-function, with the analytic and asymptotic structure of $Q(\nu)$ tightly linked to the meson spectrum.

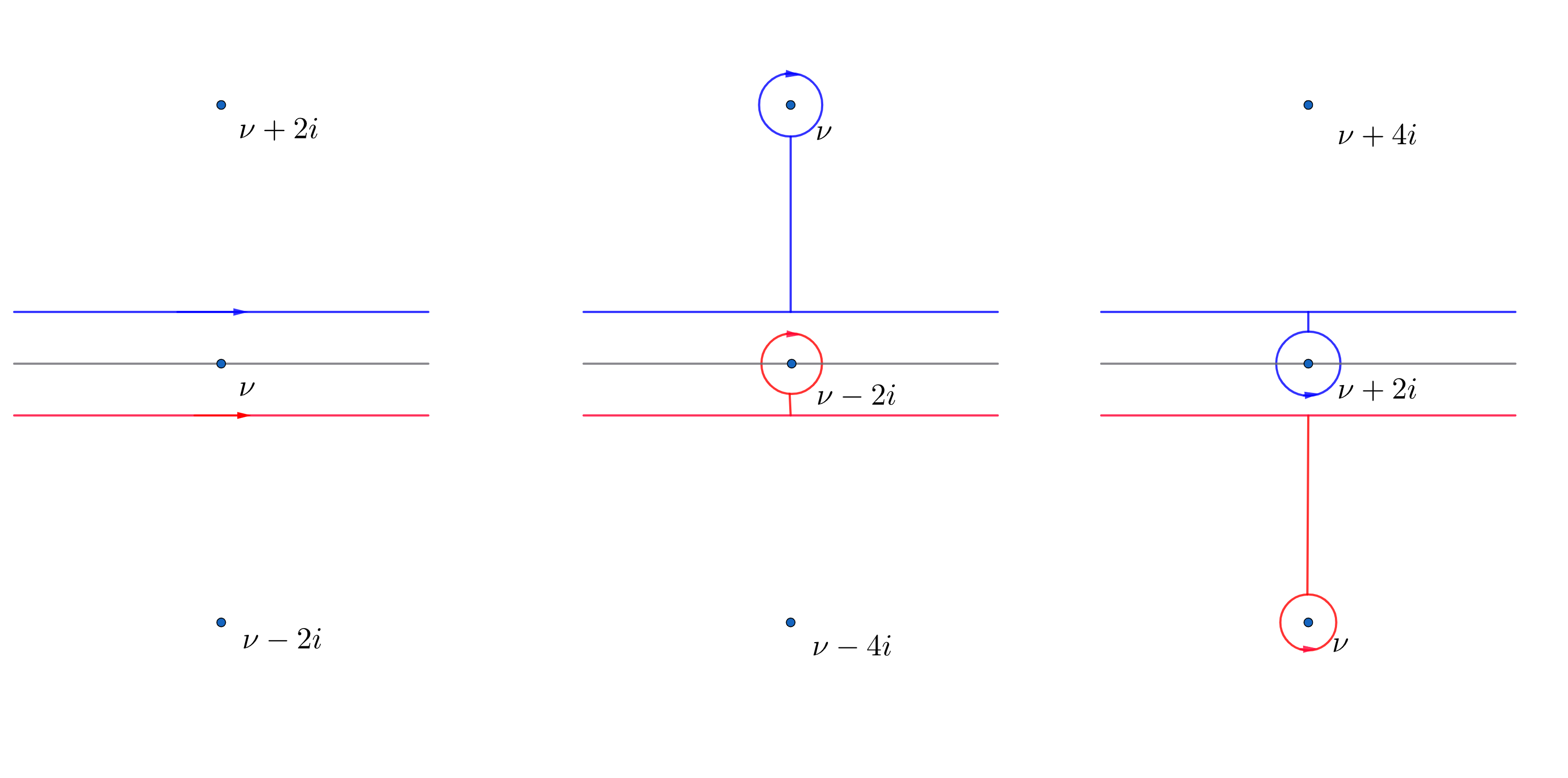
Figure 1: Analytic continuation $\nu \to \nu \pm 2i$ from the real axis introduces additional terms due to residue contributions from poles crossing the principal value integration path.

The main technical result is that, by tracking the analytic properties of $Q(\nu)$ (namely, its periodicity, boundedness, and location of zeros/poles), the quantization conditions on the meson spectrum are encoded in these analytic constraints. The $Q$-function formalism naturally generates spectral determinants whose zeros coincide with meson masses.

Solution Methods and Spectral Data

Small and Large Coupling Expansions

The authors develop two complementary expansions for the $Q$-functions:

• Small-$\lambda$ expansion: Yields analytic information about low-lying meson states via iterative solution of the TQ equation as a power series. Coefficients are nontrivial meromorphic functions in the Fourier variable, and all unwanted poles are removed via careful linear combinations.
• Large-$\lambda$ (WKB) expansion: Provides the basis for a systematic $1/n$ (large quantum number) expansion, capturing asymptotic Regge behavior and finer logarithmic corrections. Closed-form WKB expressions are constructed up to high order, accurately tracking the dependence of the meson spectrum on the mass parameters.

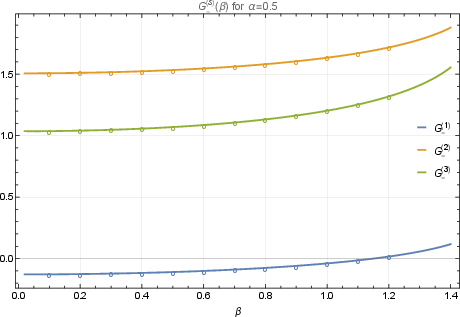
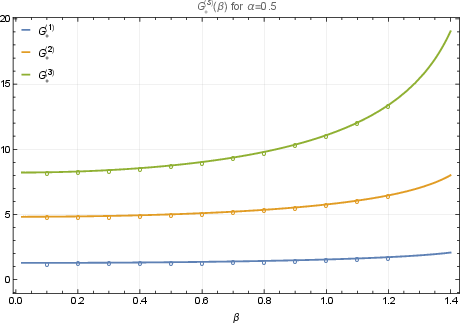
Figure 2: Illustration of spectral sum structure $G^{(s)}$, capturing the summed inverse powers of the meson eigenvalues, which are essential for both sum rule consistency and as high-precision observables for numerical checks.

Spectral Determinants, Sums, and Quantization Conditions

The meson masses coincide with zeros of spectral determinants $D_\pm(\lambda)$ for even/odd parity sectors, whose logarithms generate all spectral sums. The authors formulate Wronskian-type identities and relate log-derivatives of $Q$-functions to the derivatives of the spectral determinants. These relations enable extraction of explicit, non-perturbative formulas for the spectral sums and their dependence on the mass asymmetry.

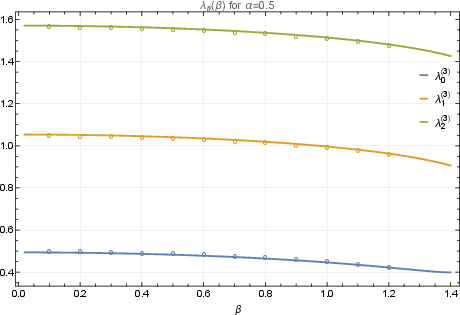
Figure 3: Eigenvalues $\lambda_n(\beta)$ for $\alpha = 0.5$; continuous lines show the analytic WKB predictions, and circles are numerical results. Agreement across a range of $\beta$ confirms the structure of the large-$n$ expansion.

The WKB expansion of the meson spectrum takes the form:

$$\lambda_n = \frac{1}{2}\mathfrak{n} + \frac{\alpha}{\pi^2}\log \rho + \text{corrections}(\mathfrak{n})$$

with detailed dependence on the quark mass parameters $\alpha, \beta$. The expansion correctly reproduces Regge trajectories and quantization patterns, and generalizes established results for the equal-mass scenario.

Strong Numerical Validation and Limiting Case Analysis

Extensive numerical results validate the analytical expressions to high accuracy. This includes checks of the spectral sums, eigenvalue expansions, and the ratios of spectral determinants. Notably, the comparison holds uniformly across varied mass asymmetries, highlighting the robustness of the analytic continuation and expansion schemes.

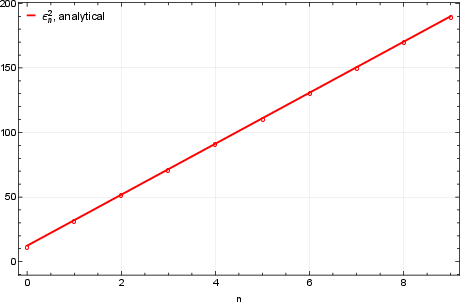
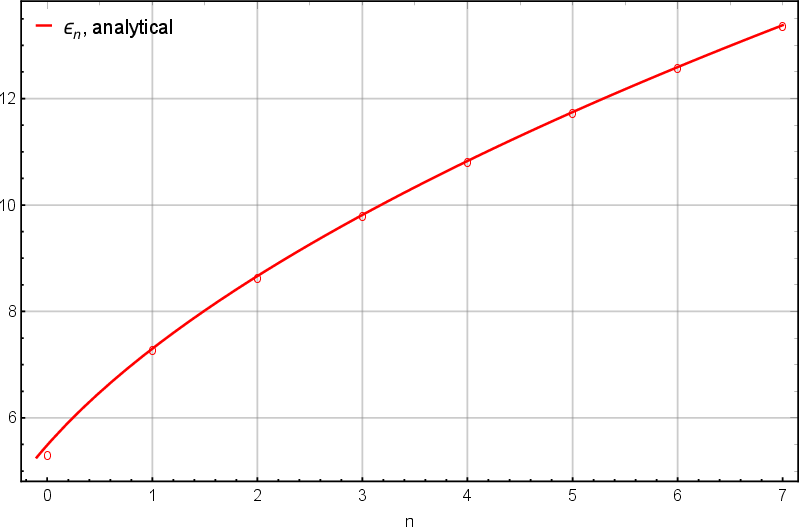
Figure 4: Corrections to meson masses $M_n$ in the heavy-light limit; left, case $\alpha_1 = 0$ for first 10 levels; right, case $\alpha_1 = 3$ for first 8 levels. Circles are numerical results; continuous lines are analytic predictions.

Limiting cases analyzed include:

• The chiral limit ($\alpha_i \to -1$): Recovery of a massless Goldstone boson and divergence of certain spectral sums, in agreement with the GMOR relation.
• The heavy quark limit ($\alpha, \beta \gg 1$): Leading and subleading scaling of spectral sums and spectrum match with semiclassical and non-relativistic expectations.
• The heavy-light limit, where one quark is much heavier than the other: Correct reproduction of square-root energy splittings and matching with known heavy-light integral equation asymptotics.

Theoretical and Practical Implications

Analytically tractable expressions for the two-flavor meson spectrum in the 't Hooft model have implications on several fronts:

• Model Integrability: The persistence of the integrable structure under mass deformation suggests hidden algebraic symmetries may underpin more general gauge theories, notably providing a bridge to the spectral theory of quantum curves in related 2D gauge or string systems.
• Sum rule observables: Analytic spectral sums serve as benchmarks for nonperturbative studies of meson observables and can assist in the calibration of numerical methods in Hamiltonian truncation and related approaches.
• Universal features and Regge behavior: The systematization of $1/n$-corrections, logarithmic violations of exact linear Regge trajectories, and the interleaving of even/odd parity states enable precise paper of two-flavor bound states in lower-dimensional QCD, including string-breaking and heavy-light transitions.

Speculatively, the techniques developed may inspire analytic progress in more complex models, including adjoint QCD$_2$, higher-dimensional toy models, or models where integrability is emergent in the infrared. They also provide a field-theoretic laboratory for the paper of quantum integrable difference equations and connections to spectral theory in mathematical physics.

Conclusion

This work systematically extends the analytic control over the QCD$_2$ meson spectrum to the most general two-flavour mass configuration, uncovering the continuing role of integrable structures and Baxter-type TQ equations. The presented analytic expansions, spectral sum identities, and explicit numerical validation consolidate the 't Hooft model as an exceptionally rich and analytically tractable environment. Directions for future research include extending form factor analysis, leveraging connections to lattice integrability, and exploring implications for adjoint QCD models and related quantum gauge systems.