Low-rank bias, weight decay, and model merging in neural networks (2502.17340v2)

Abstract: We explore the low-rank structure of the weight matrices in neural networks at the stationary points (limiting solutions of optimization algorithms) with $L2$ regularization (also known as weight decay). We show several properties of such deep neural networks, induced by $L2$ regularization. In particular, for a stationary point we show alignment of the parameters and the gradient, norm preservation across layers, and low-rank bias: properties previously known in the context of solution of gradient descent/flow type algorithms. Experiments show that the assumptions made in the analysis only mildly affect the observations. In addition, we investigate a multitask learning phenomenon enabled by $L2$ regularization and low-rank bias. In particular, we show that if two networks are trained, such that the inputs in the training set of one network are approximately orthogonal to the inputs in the training set of the other network, the new network obtained by simply summing the weights of the two networks will perform as well on both training sets as the respective individual networks. We demonstrate this for shallow ReLU neural networks trained by gradient descent, as well as deep linear networks trained by gradient flow.

• The paper reveals that L2 weight decay induces a low-rank bias in network weights, which facilitates effective parameter sharing through model merging.
• It combines rigorous theoretical analysis with experiments on models like BERT and GPT-2 to validate the role of low stable ranks in multitask learning.
• The study demonstrates a computationally efficient strategy for merging models trained on orthogonal tasks, opening avenues for scalable multi-task and distributed learning.

Low-rank Bias, Weight Decay, and Model Merging in Neural Networks

This essay analyzes the paper titled "Low-rank bias, weight decay, and model merging in neural networks" (2502.17340), which explores the low-rank structures of weight matrices in neural networks influenced by $L2$ regularization, commonly referred to as weight decay. The paper reveals properties of these structures and their influence on a multitask learning phenomenon known as model merging. The researchers demonstrate how these concepts enable a unique form of parameter sharing across neural networks trained on distinct tasks, paving the way for new insights in efficient neural network training and multitask learning.

Introduction

The behavior of first-order optimization algorithms, particularly SGD, has been extensively studied in contexts involving convexity or weak non-convexity. However, in the domain of overparameterized deep neural networks, understanding the role of implicit biases, particularly concerning $L2$ regularization, is crucial. Such regularization leads to low-rank bias in neural network weight matrices, aligning parameters with gradients and preserving norms across layers. The paper focuses on how this low-rank bias facilitates model merging, a multitask learning strategy where the summation of weight matrices from networks trained on orthogonal tasks results in a model proficient on both.

Theoretical Insights: Low-rank Bias

Alignment and Norm Preservation

The paper explores the alignment of parameters with gradients at the stationary points of neural networks with $L2$ regularization. It establishes norm preservation across layers for deep networks with homogeneous activation functions. This is mathematically characterized by:

$$\lambda \|W_k \|_F^2 = - \frac{H^{K-k}}{n} \sum_i \ell'(y_i f_{\theta}(x_i)) y_i f_{\theta}(x_i),$$

where $W_k$ represents weight matrices, preserving Frobenius norms across layers proportional to the homogeneity parameter $H$.

Low-rank Structure

Stable matrix ranks are notably low at these stationary points:

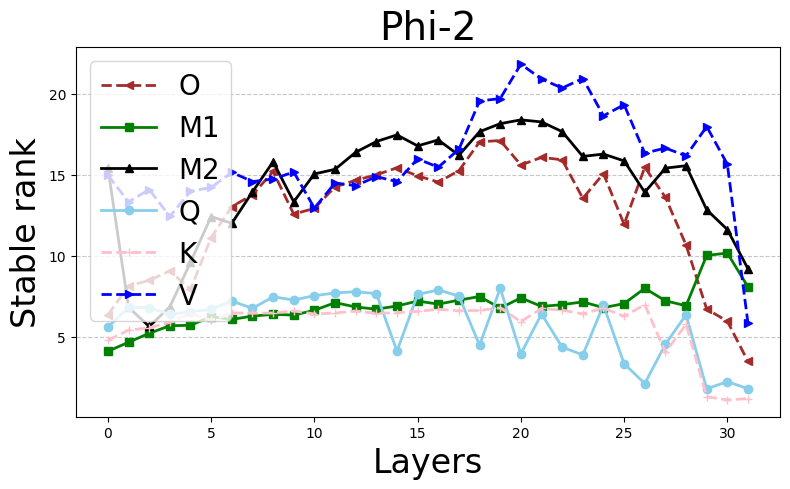
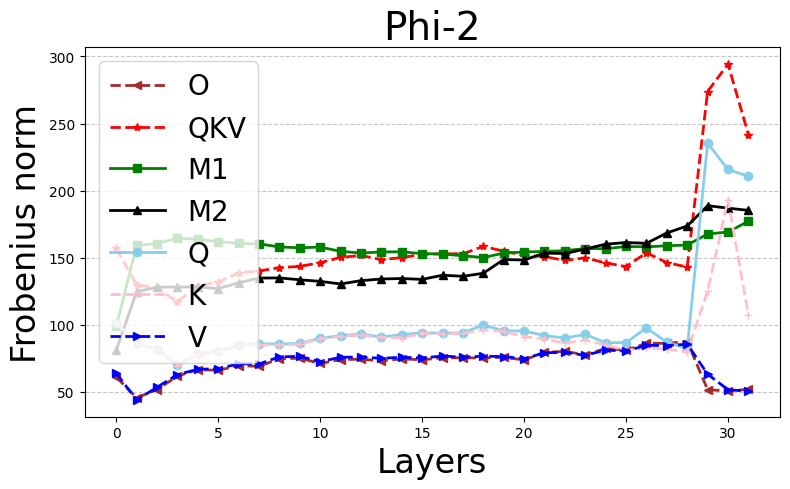
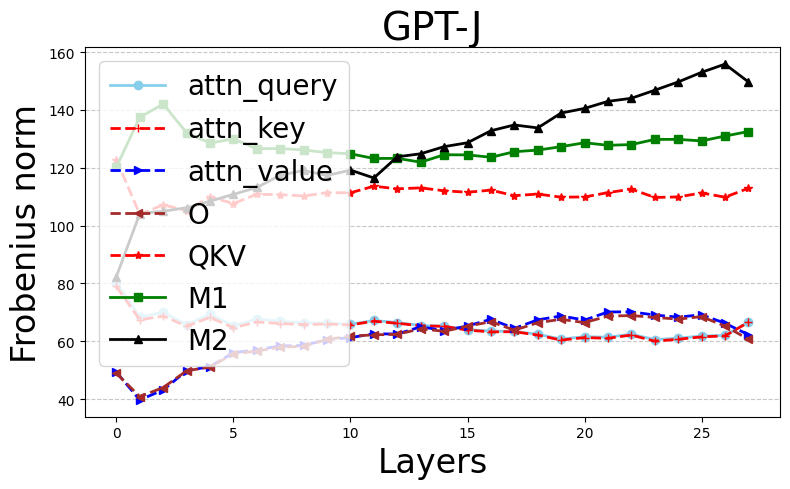
Figure 1: Stable ranks and Frobenius norms of different weight matrices in pretrained Phi-2 (first row) and GPT-J (second row) models.

The authors provide a rigorous bound on stable ranks as a function of the regularization parameter $\lambda$ and the training loss, showing that increases in $\lambda$ induce lower stable ranks. This extends even to complex architectures like transformers, albeit under certain idealized conditions.

Practical Application: Model Merging

Model merging exploits the low-rank nature of trained neural networks to efficiently integrate models trained on orthogonal datasets. The paper demonstrates that networks trained independently on distinct tasks with orthogonal inputs can merge through simple weight addition to form a new network that retains performance efficiency on both tasks.

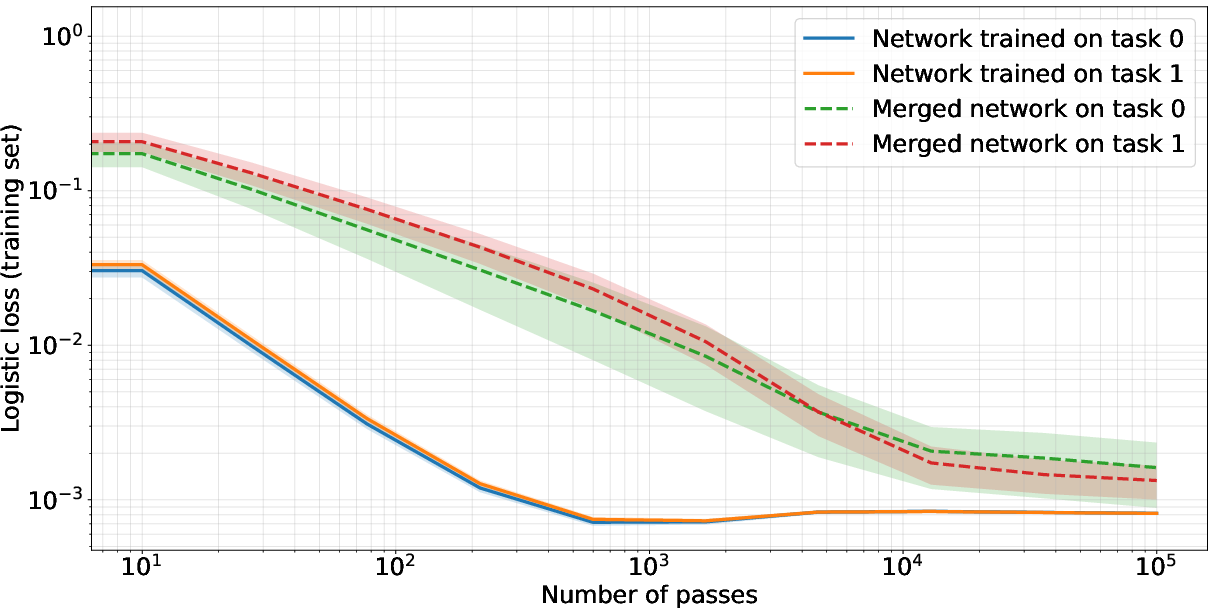
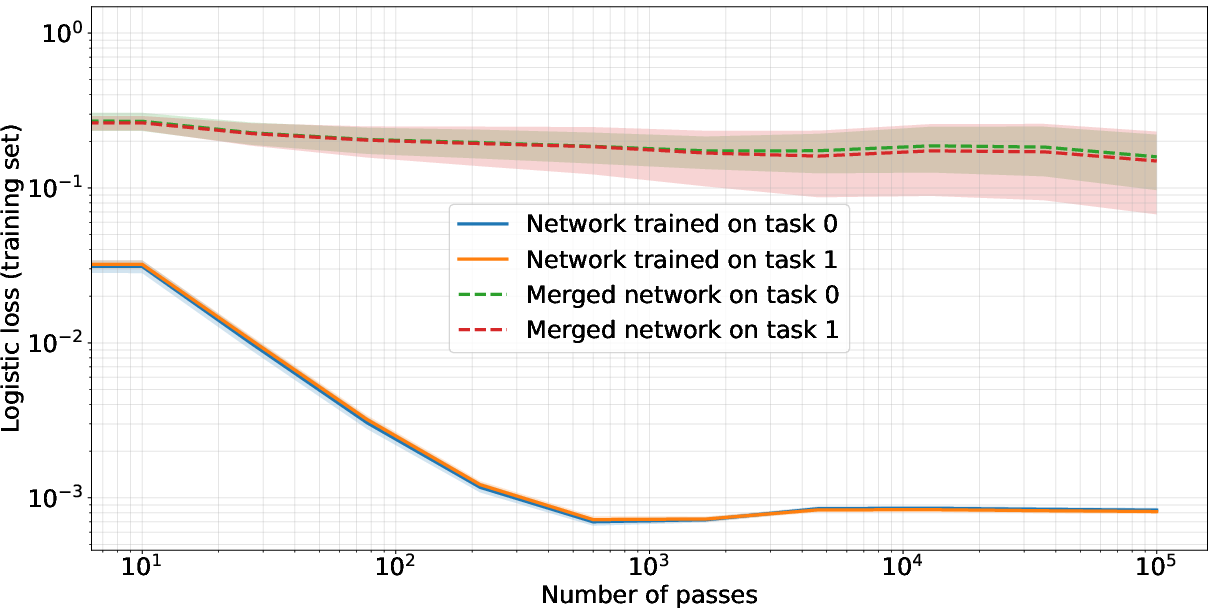
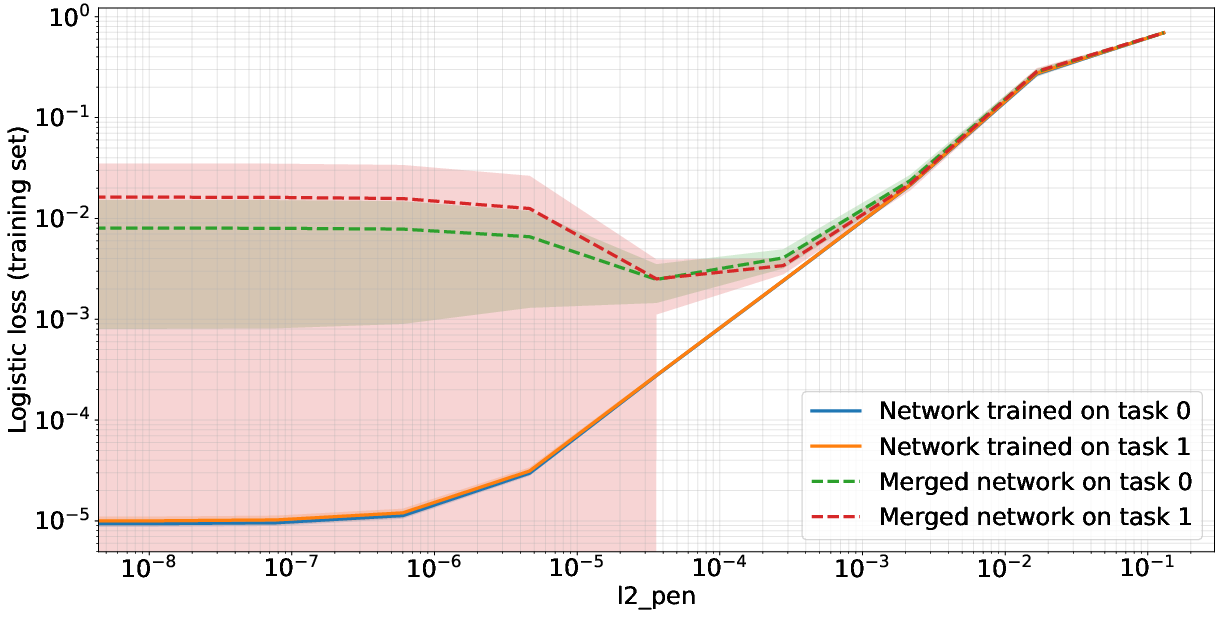
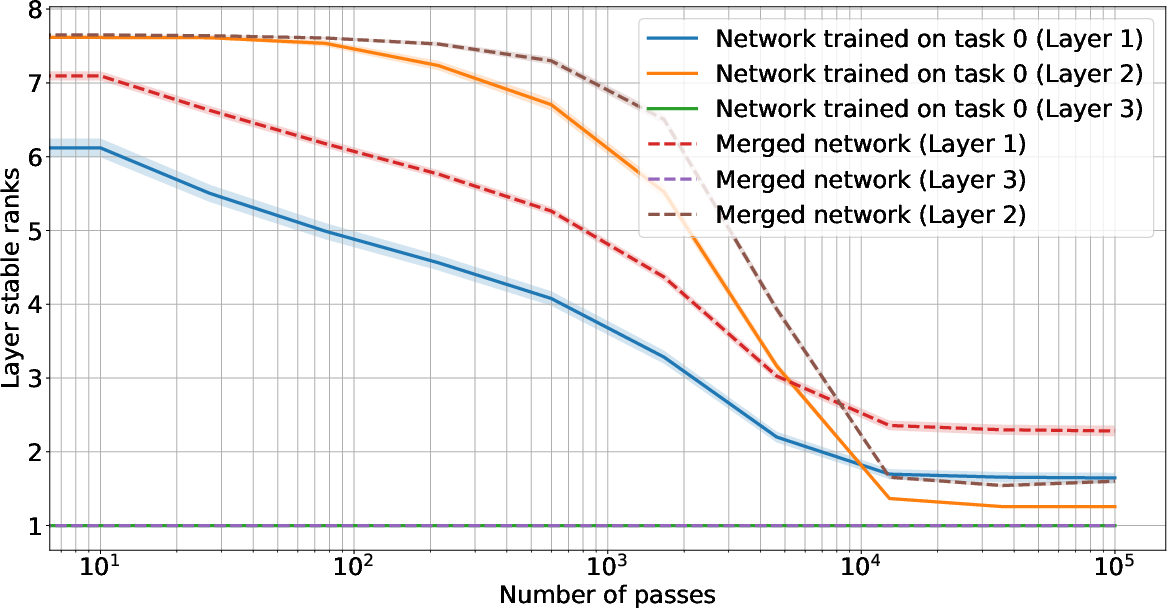
Figure 2: First row: Training neural networks on different tasks (orthogonal inputs) (left) vs. the same task (right) and merging the parameters by adding weight matrices. The resulting network performs well on different tasks after sufficiently many iterations, while given the same task, it does not. Second row: this effect manifests when weight decay strength is sufficiently large (left). Stable rank of each weight matrix converges to a small value, while stable rank of the merged network matches stable ranks of individual networks (right).

Experimental Validation

Experiments conducted on synthetic datasets and models pre-trained on popular natural language processing tasks reinforce these theoretical claims. These experiments included substantial architectures like BERT, GPT-2, and RoBERTa, which demonstrated consistent low-rank properties. Additionally, merging models trained on orthogonal tasks resulted in combined models that maintained performance across both tasks.

Conclusion

This paper provides valuable insights into the implicit regularization effects of $L2$ weight decay, elucidating its role in inducing low-rank structures in neural networks. These findings have significant implications for multitask learning paradigms, proposing a computationally efficient model merging strategy. By leveraging low-rank biases, neural networks can be adapted to multi-task scenarios with minimal architectural changes, opening possibilities for further explorations in efficient AI systems. Future research can enhance understanding and explore applications in distributed learning or collaborative AI model development.