Deep Weight Factorization: Sparse Learning Through the Lens of Artificial Symmetries (2502.02496v2)

Abstract: Sparse regularization techniques are well-established in machine learning, yet their application in neural networks remains challenging due to the non-differentiability of penalties like the $L_1$ norm, which is incompatible with stochastic gradient descent. A promising alternative is shallow weight factorization, where weights are decomposed into two factors, allowing for smooth optimization of $L_1$-penalized neural networks by adding differentiable $L_2$ regularization to the factors. In this work, we introduce deep weight factorization, extending previous shallow approaches to more than two factors. We theoretically establish equivalence of our deep factorization with non-convex sparse regularization and analyze its impact on training dynamics and optimization. Due to the limitations posed by standard training practices, we propose a tailored initialization scheme and identify important learning rate requirements necessary for training factorized networks. We demonstrate the effectiveness of our deep weight factorization through experiments on various architectures and datasets, consistently outperforming its shallow counterpart and widely used pruning methods.

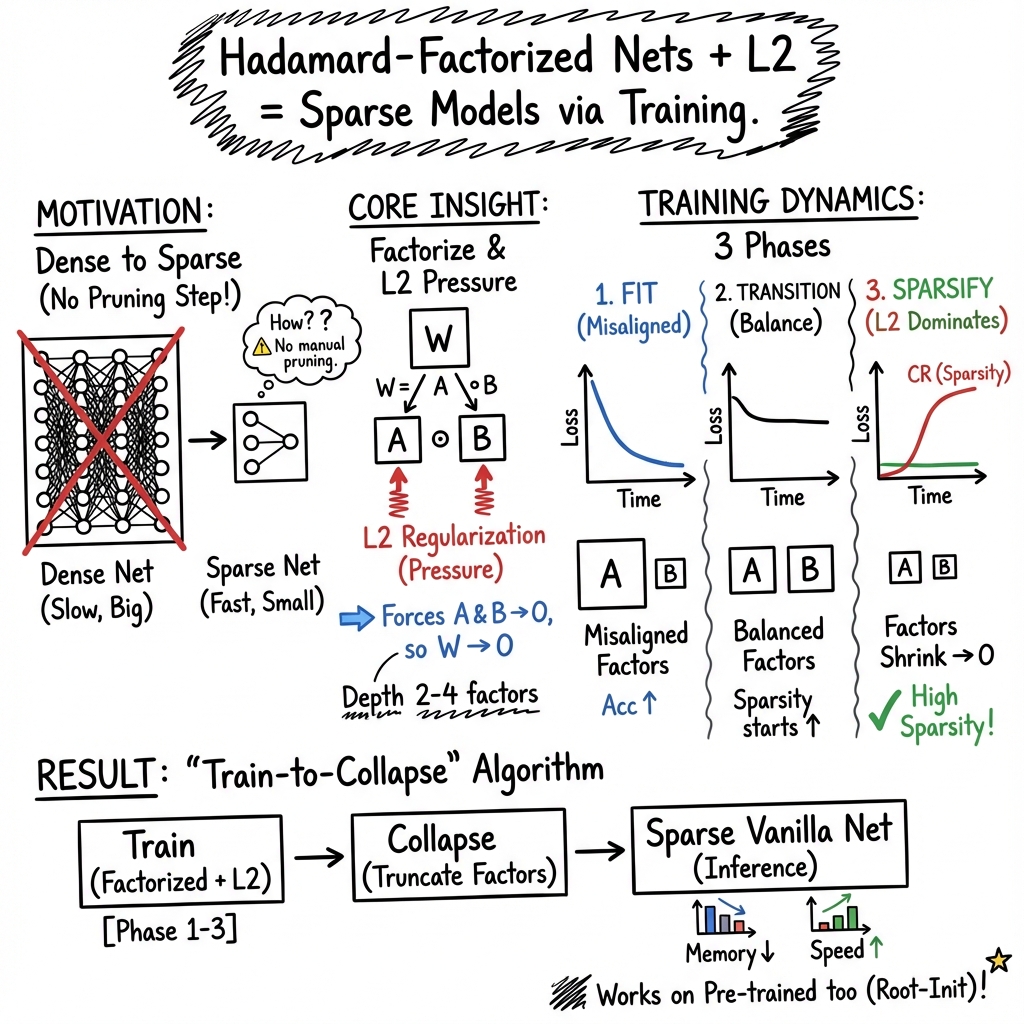
• The paper introduces Deep Weight Factorization (DWF), a novel method that leverages artificial symmetries to naturally induce sparsity through over-parameterization.
• It employs SGD dynamics to balance factor norms, enabling a transition from dense to sparse configurations without compromising accuracy.
• Experimental results on architectures such as ResNet and VGG demonstrate that DWF achieves competitive performance with reduced computational and memory overhead.

Deep Weight Factorization: Sparse Learning Through the Lens of Artificial Symmetries

Introduction

This paper introduces a novel approach in sparse learning through the development of Deep Weight Factorization (DWF), a method grounded in the artificial symmetries of neural networks. This paper addresses the challenges inherent in conventional sparse learning, such as computational inefficiencies and suboptimal model performance. By leveraging the intrinsic symmetries of the weight space, the authors present a method that not only enhances efficiency but also maximizes model accuracy while maintaining sparsity.

Methodology

The core of DWF lies in the factorization of weight matrices, which is accomplished by introducing redundancy through over-parameterization. This approach contrasts sharply with traditional methods that employ direct sparsification. Over-parameterization via DWF enables the model to reach sparse solutions through natural convergence dynamics rather than manual sparsification constraints. The model begins training without imposed sparsity and evolves its latent symmetries, aligning with desired sparse configurations spontaneously.

In the context of stochastic gradient descent (SGD) dynamics, the DWF approach ensures that once the norm of factors is balanced, sparsity naturally emerges. This dynamic is illustrated by the training phases observed in the experiments: an initial fitting phase with zero sparsity, a transitional phase where sparsity starts to manifest, and a final phase of increasing sparsity with converging compression rates.

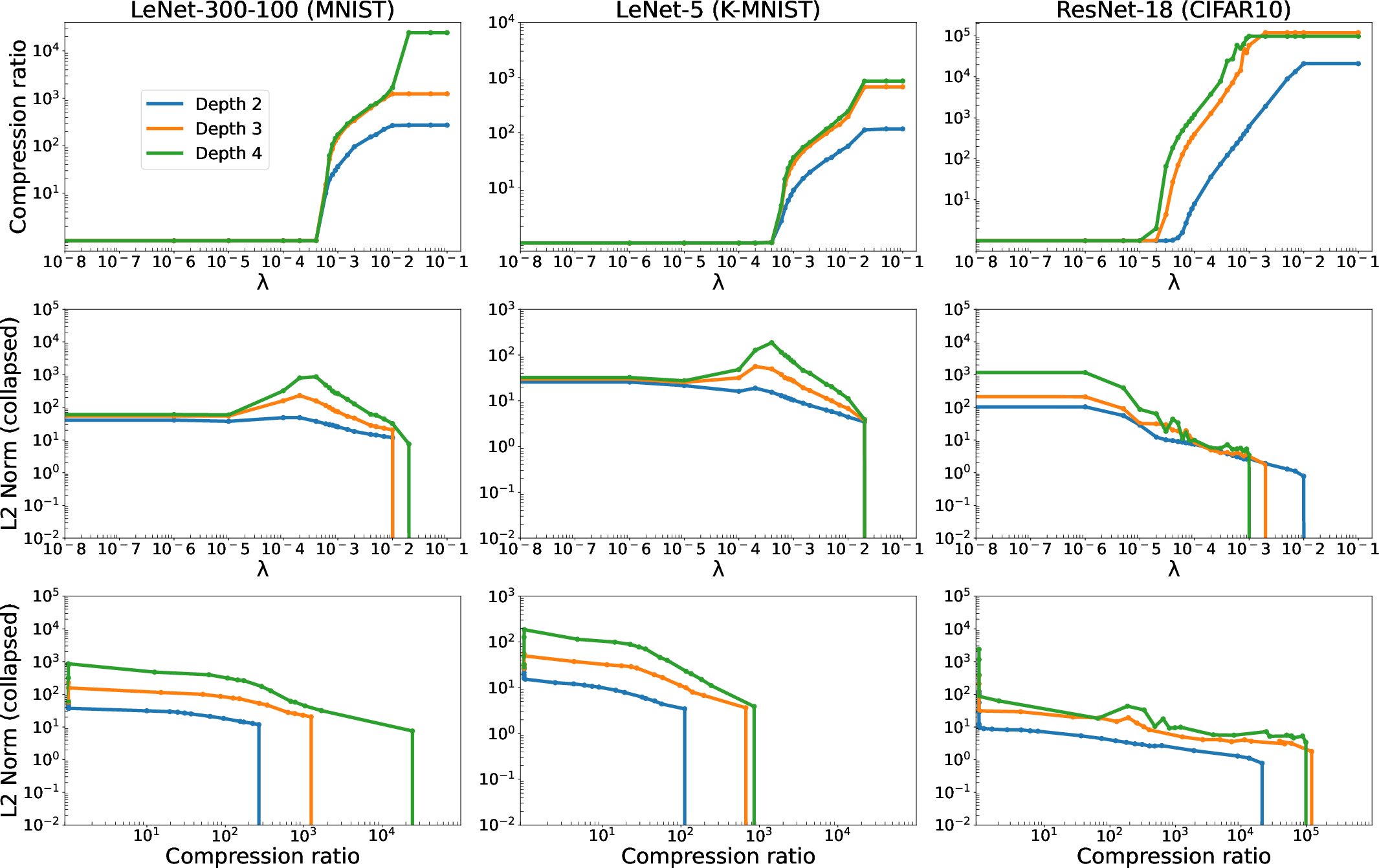
Figure 1: Trajectory of model parameters under SGD showcasing distinct phases where over-parameterization leads to emergent sparsity.

Experimental Results

The empirical evaluations deploy DWF on various architectures (e.g., ResNet, VGG) and datasets (e.g., CIFAR-10, Tiny ImageNet), demonstrating consistent performance improvements across wide tasks. Sparse representations are attained without sacrificing accuracy, as illustrated by performance trajectories during training.

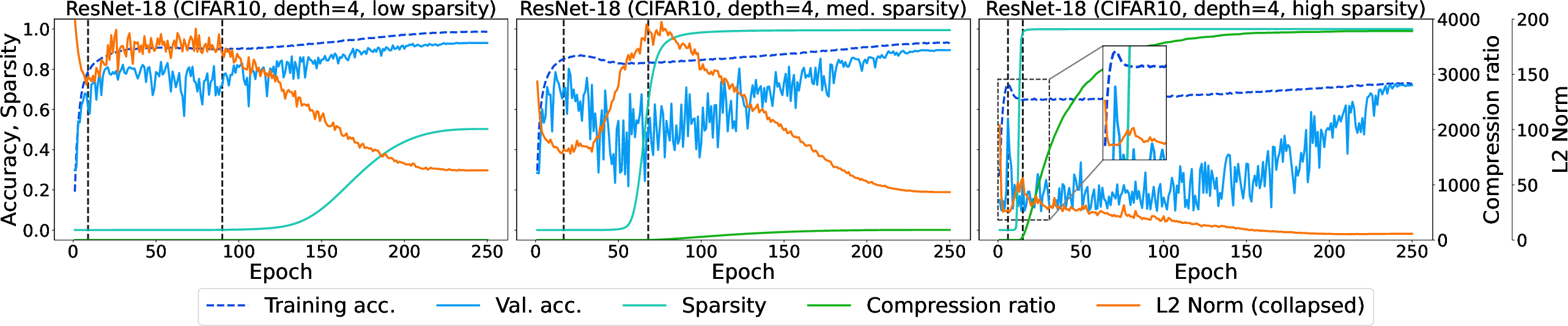
Figure 2: Dynamics of sparsity regimes in ResNet18 demonstrating the transition from dense to sparse representations.

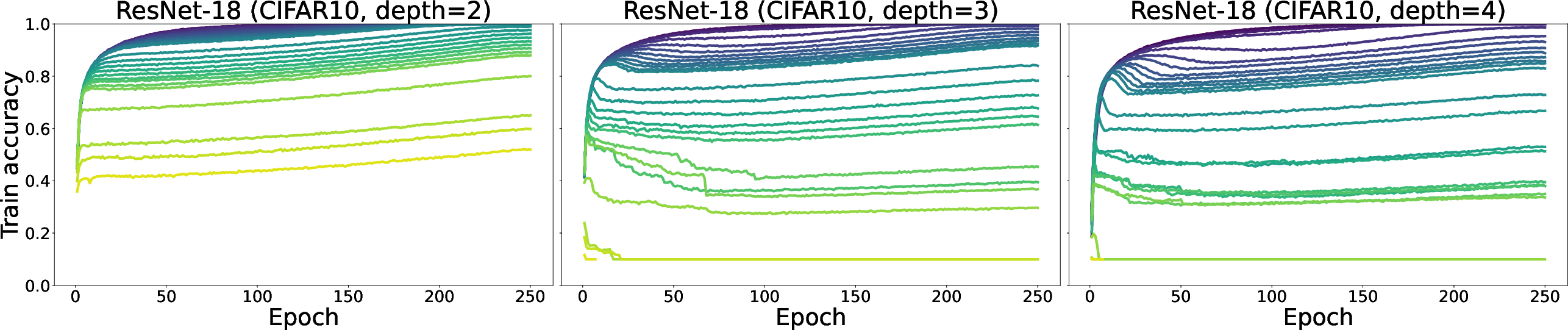
Figure 3: Training accuracy dynamics for ResNet18 on CIFAR-10 showing stability and performance across different epochs.

The results reveal that DWF achieves comparable or superior performance to state-of-the-art sparsity methods while requiring less computational overhead, particularly in memory usage and training speeds. Notably, the method handles increased data and model complexity while maintaining efficiency, indicative of its scalability and robustness.

Implications and Future Work

The findings have significant implications for the design of sparse models in deep learning, offering a mechanism that balances the trade-off between model complexity and performance with practical efficiency. By exploiting intrinsic symmetries, DWF provides a path to reduce resource consumption, which is crucial for real-world applications involving large-scale models and datasets.

Future research could explore extending DWF to various optimization algorithms, beyond SGD, and analyzing its impact on different neural architectures. Furthermore, adaptive methods that dynamically adjust factorization during training could enhance efficiency and potentially provide insights into the intrinsic geometrical structures of neural networks.

Conclusion

Deep Weight Factorization represents a significant advancement in sparse learning methodologies. By framing the problem through artificial symmetries, it introduces a paradigm shift that not only optimizes computational demands but also ensures model robustness. This work lays the foundation for future exploration into factorization techniques that could redefine efficiency standards in deep learning models.