BN-Pool: a Bayesian Nonparametric Approach to Graph Pooling

Abstract: We introduce BN-Pool, the first clustering-based pooling method for Graph Neural Networks (GNNs) that adaptively determines the number of supernodes in a coarsened graph. By leveraging a Bayesian non-parametric framework, BN-Pool employs a generative model capable of partitioning graph nodes into an unbounded number of clusters. During training, we learn the node-to-cluster assignments by combining the supervised loss of the downstream task with an unsupervised auxiliary term, which encourages the reconstruction of the original graph topology while penalizing unnecessary proliferation of clusters. This adaptive strategy allows BN-Pool to automatically discover an optimal coarsening level, offering enhanced flexibility and removing the need to specify sensitive pooling ratios. We show that BN-Pool achieves superior performance across diverse benchmarks.

• The paper introduces BN-Pool, a Bayesian nonparametric graph pooling method that adapts cluster counts per input using a Dirichlet Process prior.
• It employs a stochastic block model with a variational GNN encoder to balance adjacency reconstruction and regularization, achieving 98.5% accuracy in unsupervised node clustering.
• The approach supports both unsupervised and supervised tasks by providing flexible, end-to-end adaptive pooling that outperforms traditional fixed-parameter methods.

BN-Pool: Bayesian Nonparametric Pooling for Adaptive Graph Coarsening

Introduction

BN-Pool defines a Bayesian nonparametric (BNP) method for graph pooling in Graph Neural Networks (GNNs), addressing limitations of parametric soft-clustering pooling techniques that require predefined, fixed numbers of clusters. By employing a Dirichlet Process (DP) prior and a probabilistic generative model for graph structure, BN-Pool infers cluster assignments adaptively per-graph, thereby autonomously determining an appropriate coarsened representation aligned with each input's complexity. This formulation supports both unsupervised and supervised objectives, leveraging a GNN-based encoder for amortized posterior inference and embedding downstream task signals for end-to-end learning.

Figure 1: Graphical representation of BN-Pool, illustrating the plate notation for the generative model and dependency structure.

Bayesian Nonparametric Pooling Formulation

BN-Pool models the observed adjacency matrix as generated by a stochastic block model (SBM), where cluster assignments are latent variables governed by a DP prior. Stick-breaking construction is used to realize an (in practice, truncated) infinite mixture over possible communities:

• For each node, stick fraction variables are sampled from Beta distributions, translated via the stick-breaking process to soft cluster assignment vectors.
• Cluster-cluster edge probabilities are realized as a block matrix with intra/inter-cluster priors, parameterized for regularization and flexibility.
• Each possible edge is sampled via a Bernoulli likelihood, whose parameter depends on the corresponding cluster memberships of the endpoints.

This formalism enables adaptive cluster count per input without requiring explicit pooling ratios, in contrast to classical approaches that use fixed $K$. The posterior inference task is performed via amortized variational inference, where a GNN outputs parameters for the Beta variational distributions over stick fractions.

Figure 3: Graphical representation of the stick-breaking process underlying the DP prior used for cluster assignments.

Training, Objectives, and SEL-RED-CON Instantiation

BN-Pool is trained by maximizing a variational Evidence Lower Bound (ELBO), comprising three key terms:

• Adjacency Reconstruction: Binary cross entropy between observed edges and model predictions, representing the likelihood under the generative process.
• KL Divergence over Stick Fractions: Encourages parsimony in cluster counts per the DP prior, balancing model fit with cluster proliferation.
• KL Divergence over Cluster Connectivity: Regularizes the block matrix entries towards intra/inter-cluster structural priors.

An auxiliary loss term combines these for unsupervised training or as a regularizer alongside standard supervised losses for downstream tasks.

Figure 4: The SEL operation and auxiliary loss components, highlighting the interaction between cluster assignment inference and the ELBO decomposition.

BN-Pool cleanly fits into the Select-Reduce-Connect (SRC) graph pooling decomposition:

• SEL: Truncated stick-breaking SEL yields soft assignment matrix $S \in \mathbb{R}^{N \times C}$ (with $K \leq C$ non-empty clusters).
• RED: Coarsened features computed as $X_\text{pooled} = S^\top X$.
• CON: Pooled adjacency computed as $A_\text{pooled} = S^\top A S$, followed by normalization.

Empirical Evaluation: Clustering and Classification

Unsupervised Node Clustering

On the synthetic Community and real-world citation datasets, BN-Pool demonstrates consistently high cosine similarity and classification accuracy (ACC) when its unsupervised assignments are compared against ground-truth classes, despite the lack of supervision regarding the number of clusters. On Community, BN-Pool achieves 98.5% ACC, outperforming parametric competitors while discovering a number of clusters aligned with true community structure, and autonomously splitting or aggregating communities as appropriate.

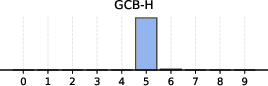
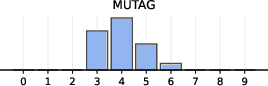
Figure 6: Distribution of non-empty clusters discovered across different datasets, demonstrating the adaptive nature of BN-Pool in varying topologies.

Visualization of assignment matrices and reconstructed adjacencies show BN-Pool achieves fine-grained, structurally-faithful partitions, accurately recovering small and large communities—even in low-density, sparse homophilic regimes—unlike approaches that enforce balanced clusters or fixed $K$.

Supervised Graph Classification

BN-Pool achieves uniformly strong ROC-AUC/accuracy across a broad suite of TU datasets (e.g., Colors3, GCB-H, molhiv), typically matching or surpassing best-in-class soft clustering alternatives and exhibiting a dramatic lead in challenging settings (e.g., 93% accuracy on Colors3, considerably higher than all baselines). On homophilic datasets, node-to-supernode assignments nearly perfectly align with semantic or feature classes, as seen in GCB-H.

Figure 7: Comparison between original node features and BN-Pool cluster assignments on GCB-H, illustrating nearly exact matching.

Critically, the adaptivity of BN-Pool is visible in the wide distribution of pooled graph sizes per sample (see Figure 5 above) and its superior ability to compactly represent both small and large graphs without manual tuning of pooling hyperparameters.

Theoretical and Practical Implications

BN-Pool’s Bayesian nonparametric design has significant implications:

• Flexibility and Generalization: Automatic cluster count adaptation eliminates the need for manual pooling ratio search or parameter tuning required by parametric or score-based alternatives.
• Principled Structural Inductive Bias: The DP and SBM-based priors encode a probabilistically justified preference for parsimony and community structure, regularizing representation and mitigating overfitting to noisy or idiosyncratic patterns.
• End-to-end Adaptation: The variational GNN encoder allows downstream tasks to shape the pooling granularity as needed for the current objective, while maintaining effective unsupervised signal via auxiliary likelihoods.

Practically, BN-Pool is suitable for large-scale and highly heterogeneous datasets, addressing limitations found in clinical graphs, molecular structures, and dynamic networks where a universal granularity is unattainable.

Future Directions

The framework is naturally extensible to:

• Heterophilic graph contexts, via modified block matrix priors or GNN encoders specialized for non-assortative structures.
• Overlapping or mixed membership clustering, by relaxing exclusivity constraints in assignments.
• Efficient amortized inference and scalable implementations for dynamic or streaming graphs, exploiting recent progress in stochastic variational and implicit gradient estimation.
• Incorporation into more expressive or equivariant GNN architectures for higher-order structure modeling.

The Bayesian nonparametric methodology offers a composable backbone for integrating additional generative priors or hierarchical structures, pointing toward progressively more adaptive and interpretable GNN designs.

Conclusion

BN-Pool formalizes a Bayesian nonparametric approach to graph pooling, leveraging the stick-breaking construction of the DP within a structured generative model for adjacency. It achieves adaptive pooling, strong unsupervised and supervised performance, and demonstrates the value of probabilistic nonparametrics for flexible and robust GNN architecture design. The results underline its promise as a default choice for complex, variable-size graph learning tasks, and motivate exploration of further BNP-driven advances in graph representation learning (2501.09821).