EGPT-PINN: Entropy-enhanced Generative Pre-Trained Physics Informed Neural Networks for parameterized nonlinear conservation laws

Abstract: We propose an entropy-enhanced Generative Pre-Trained Physics-Informed Neural Network with a transform layer (EGPT-PINN) for solving parameterized nonlinear conservation laws. The EGPT-PINN extends the traditional physics-informed neural networks and its recently proposed generative pre-trained strategy for linear model reduction to nonlinear model reduction and shock-capturing domains. By utilizing an adaptive meta-network, a simultaneously trained transform layer, entropy enhancement strategies, implementable shock interaction analysis, and a separable training process, the EGPT-PINN efficiently captures complex parameter-dependent shock formations and interactions. Numerical results of EGPT-PINN applied to the families of inviscid Burgers' equation and the Euler equations, parameterized by their initial conditions, demonstrate the robustness and accuracy of the proposed technique. It accurately solves the viscosity solution via very few neurons without leveraging any {\it a priori} knowledge of the equations or its initial condition. Moreover, via a simple augmentation of the loss function by model-data mismatch, we demonstrate the robustness of EGPT-PINN in solving inverse problems more accurately than the vanilla and entropy-enhanced versions of PINN.

• The paper introduces the VGPT-PINN framework, integrating a transform layer and viscosity strategies to solve parameterized nonlinear conservation laws.
• The paper demonstrates that VGPT-PINN accurately captures shock dynamics and converges rapidly with minimal neuron configurations in both 1D and 2D cases.
• The paper highlights the framework's potential for efficient model order reduction in hyperbolic PDEs and its applicability to complex flow problems.

"VGPT-PINN: Viscosity-enhanced Generative Pre-Trained Physics Informed Neural Networks for parameterized nonlinear conservation laws"

Introduction

The paper introduces the VGPT-PINN framework, a viscosity-enhanced generative pre-trained physics-informed neural network designed to solve parameterized nonlinear conservation laws. This technique extends conventional PINNs with enhancements like a transform layer, viscosity strategies, and a separable training process to efficiently capture intricate shock formations and interactions in scenarios governed by nonlinear conservation laws.

Network Architecture

VGPT-PINN builds on the traditional PINN architecture by integrating a transform layer and an adaptive meta-network. The transform layer facilitates the proper alignment of shocks and discontinuities across different parameterized states. This is crucial for model order reduction in hyperbolic PDEs where fixed structures typically fail. The architecture aims to efficiently solve equations like the inviscid Burgers' and Euler equations through a reduced setup without requiring prior knowledge about the equations.

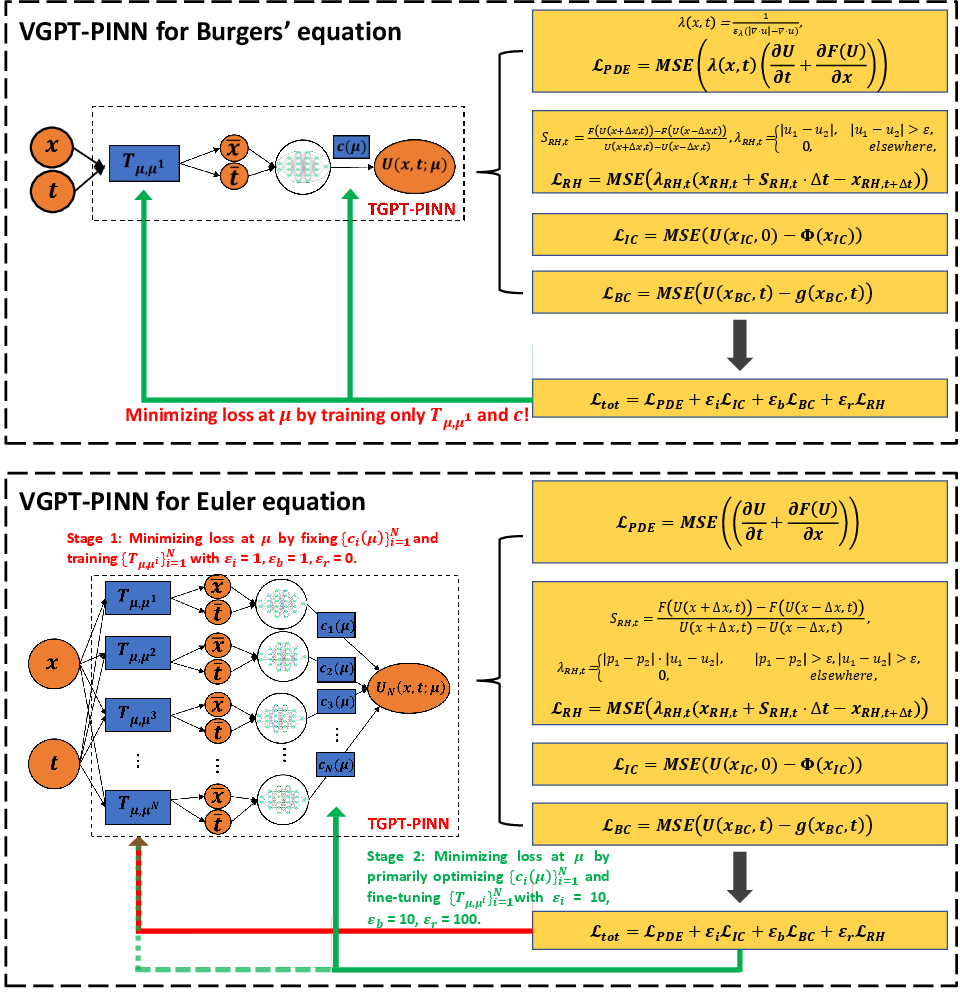
Figure 1: The VGPT-PINN design schematic for Burgers' (top) and Euler (bottom) equations. For any given parameter value $\mu$, a $\mu$-dependent loss is constructed and the coefficients $\{c_i(\mu)\}_{i=1}^n$ and the weights and biases in $\{\mathcal{T}_{\mu,\mu^i}\}_{i=1}^n$ are trained.

Loss Function and Viscosity Enhancement

An integral part of the VGPT-PINN is its sophisticated loss function which integrates the viscosity effect. The loss function comprises weighted terms for the PDE, initial and boundary conditions, as well as the Rankine–Hugoniot condition. This comprehensive design addresses overfitting near discontinuities and enhances the network's ability to capture physically accurate shock dynamics. A notable component is the inclusion of a shock detection indicator, which focuses the model’s resources on regions with high-impact discontinuities.

Numerical Experiments and Results

1D Burgers' and Euler Equations

The VGPT-PINN was evaluated on several benchmark cases, including scenarios with single and multiple shocks, rarefaction waves, and shock-wave interactions. Across five significant Burgers' equation test cases, VGPT-PINN demonstrated it can achieve precision with a minimal neuron configuration. Similarly, for the 1D Euler equations, the VGPT-PINN exhibited a rapid convergence and accurately modeled complex interactions with as few as three neurons.

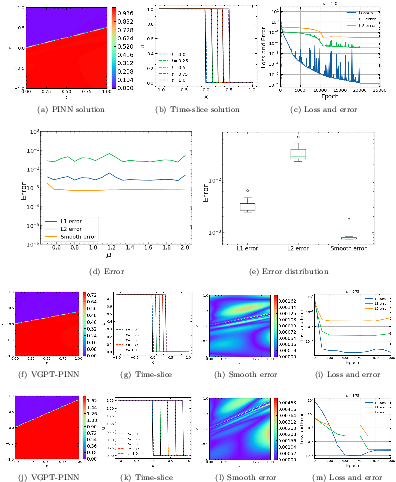
Figure 2: Results of Case ${\rm B_{1S}$ demonstrating VGPT-PINN’s accuracy in capturing single shock propagation.

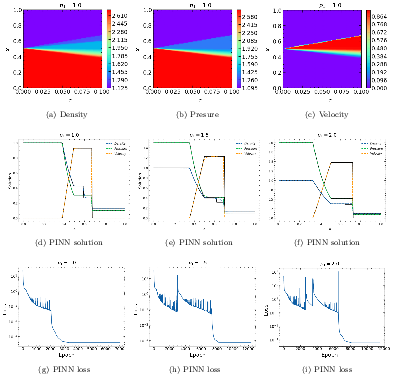
Figure 3: PINN results for the Sod problem. (a-c) $x-t$ solution for $p_1 = 1.0, (d-f) comparison with a reference solution.

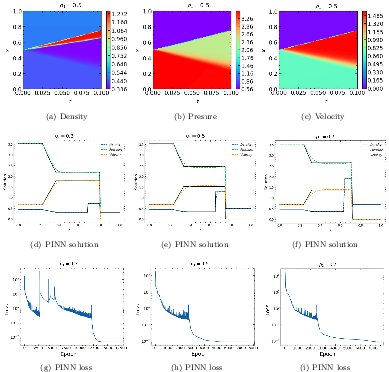
Figure 4: PINN results for the Lax problem. Demonstrates handling of strong shocks and contact discontinuities.

2D Euler Equations

For 2D problems, VGPT-PINN achieved promising performance in modeling transonic flow through a cylinder, capturing dynamics precisely with small network sizes. This exemplifies its capability to address high-dimensional parametric PDEs efficiently.

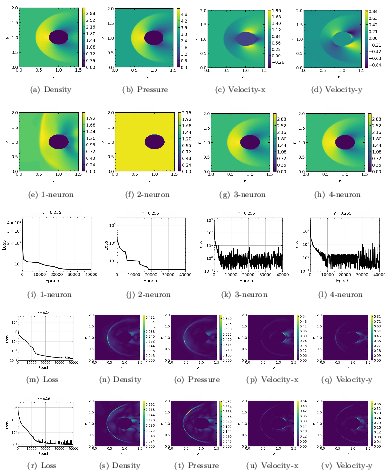
Figure 5: PINN and VGPT-PINN results for 2D Euler equations. The network efficiently handles density profiles and established shock dynamics.

Conclusion

VGPT-PINN represents a significant advancement in the use of neural networks for the solution of complex PDEs with nonlinear conservation laws. The incorporation of viscosity effects and sophisticated loss functions allows this model to achieve high accuracy and robustness with significantly reduced computation, opening pathways to efficient network-based solvers for a wide range of applications in science and engineering. Future work may explore extending this approach to more generalized multidimensional spaces and integrating hybrid models that combine data-driven methods with traditional numerical techniques for even greater efficiency and accuracy.