Covariance Matrix Adaptation Evolution Strategy for Low Effective Dimensionality (2412.01156v1)

Abstract: Despite the state-of-the-art performance of the covariance matrix adaptation evolution strategy (CMA-ES), high-dimensional black-box optimization problems are challenging tasks. Such problems often involve a property called low effective dimensionality (LED), in which the objective function is formulated with redundant dimensions relative to the intrinsic objective function and a rotation transformation of the search space. The CMA-ES suffers from LED for two reasons: the default hyperparameter setting is determined by the total number of dimensions, and the norm calculations in step-size adaptations are performed including elements on the redundant dimensions. In this paper, we incorporate countermeasures for LED into the CMA-ES and propose CMA-ES-LED. We tackle with the rotation transformation using the eigenvectors of the covariance matrix. We estimate the effectiveness of each dimension in the rotated search space using the element-wise signal-to-noise ratios of the mean vector update and the rank-$μ$ update, both of which updates can be explained as the natural gradient ascent. Then, we adapt the hyperparameter using the estimated number of effective dimensions. In addition, we refine the cumulative step-size adaptation and the two-point step-size adaptation to measure the norms only on the effective dimensions. The experimental results show the CMA-ES-LED outperforms the CMA-ES on benchmark functions with LED.

• The paper presents CMA-ES-LED, an enhanced algorithm that adapts hyperparameters based solely on effective dimensions to improve optimization on LED problems.
• It employs eigenvector-based SNR estimation and refined norm calculations to isolate contributions from effective dimensions in rotated search spaces.
• Experimental results demonstrate reduced function evaluations and higher success rates compared to traditional CMA-ES, even with redundant dimensions.

Covariance Matrix Adaptation Evolution Strategy for Low Effective Dimensionality

Introduction

The paper, "Covariance Matrix Adaptation Evolution Strategy for Low Effective Dimensionality" (2412.01156), addresses the challenges posed by high-dimensional black-box optimization problems, particularly when these problems exhibit low effective dimensionality (LED). LED is characterized by objective functions that involve redundant dimensions, which degrade the efficacy of optimization strategies like the covariance matrix adaptation evolution strategy (CMA-ES). The authors propose a modified version, CMA-ES-LED, which incorporates countermeasures for LED by adapting hyperparameters based on the effective number of dimensions and refining norm calculations to isolate contributions from effective dimensions.

Problem Definition

The LED problem involves objective functions where only a subset of dimensions significantly influences the optimization task. This imbalance arises when a rotation matrix transforms the search space, introducing redundant dimensions that do not affect the objective function's evaluation. Hence, a strategy tailored to accurately estimate and focus optimization efforts on these effective dimensions is essential.

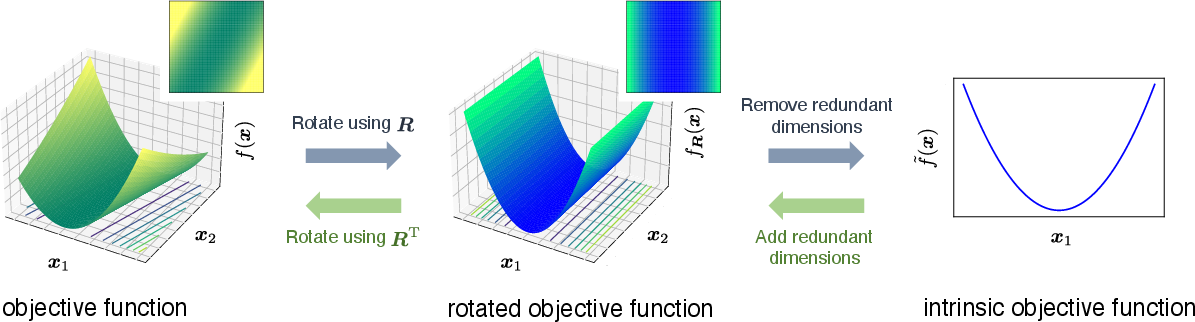
Figure 1: The conceptual image of function with LED. We simply consider the case where the objective function contains a rotation matrix $R \in R^{N \times N}$.

Proposed Method

Estimation of Effectiveness

The authors derive the effectiveness of each dimension by estimating the signal-to-noise ratios (SNRs) of update directions in rotated search spaces using the eigenvectors of the covariance matrix. Incorporating the rotation matrix's eigenvectors as part of the adaptation process allows for a refined calculation of the evolution paths, focusing on effective dimension contributions.

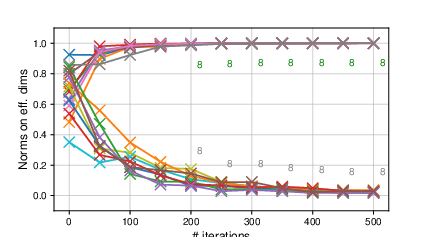
Figure 2: The transitions of the norms of rotated eigenvectors of the covariance matrix on the effective dimensions $\|\bar{\boldsymbol{b}}_i\|_\mathrm{eff}$.

Hyperparameter Adaptation

CMA-ES-LED adapts hyperparameters traditionally set based on total dimensions to reflect only the number of effective dimensions, improving search efficiency on LED problems. This adaptation is critical as traditional CMA-ES setups are adversely affected by the inclusion of redundant dimensions.

Norm Calculation Refinement

For step-size adaptation, the proposed method modifies the cumulative step-size adaptation (CSA) and the two-point step-size adaptation (TPA) to measure norms solely across effective dimensions. This ensures that redundant dimensions do not skew the optimization dynamics and the adaptations are focused where they can be most effective.

Experimental Results

Testing on benchmark functions with LED revealed significant improvements in function evaluations and success rates compared to the conventional CMA-ES. The results showed consistent performance gains, particularly when the number of redundant dimensions increased, affirming the efficacy of CMA-ES-LED's specialized adaptations.

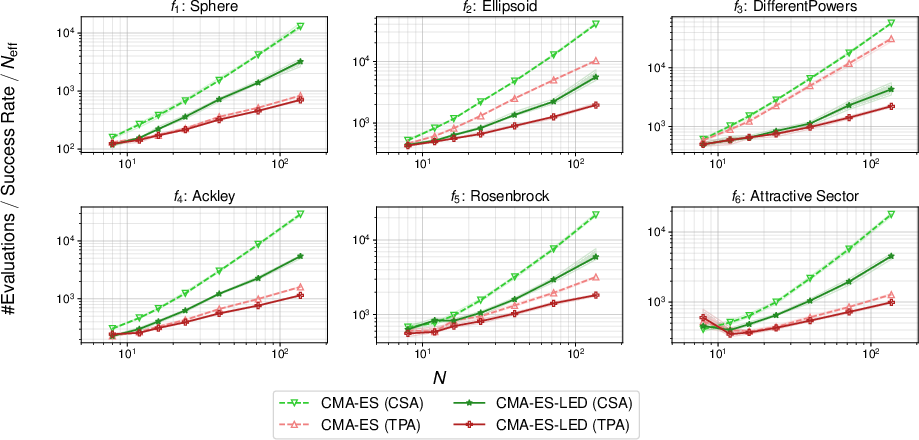
Figure 3: Comparison of the number of function evaluations divided by the success rate and the number of effective dimensions on the benchmark functions with redundant dimensions.

Additionally, when applied to benchmark functions without LED, CMA-ES-LED did not show degradation in performance, highlighting its robustness across diverse problem landscapes devoid of LED characteristics.

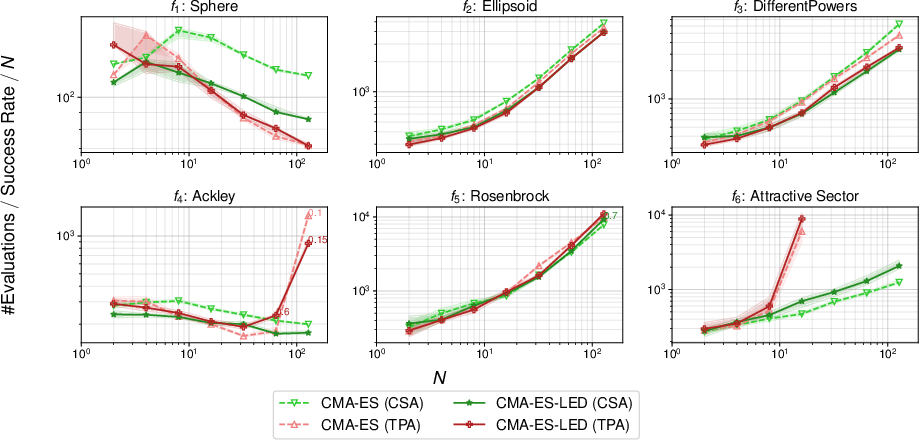
Figure 4: Comparison of the number of function evaluations divided by the success rate and the number of dimensions on the benchmark functions without redundant dimensions.

Conclusion

The paper presents a compelling approach to enhancing the CMA-ES algorithm through strategic adaptations that address the intrinsic challenges posed by LED properties. By recalibrating hyperparameters and refining step-size adaptations, CMA-ES-LED demonstrates clear advantages in both LED and non-LED environments. The research opens pathways for further exploration into combining these strategies with population size adaptations and other modifications to broaden forthcoming applications in machine learning hyperparameter optimization and complex control systems.