A block-acoustic preconditioner for the elastic Helmholtz equation

Abstract: We present a novel block-preconditioner for the elastic Helmholtz equation, based on a reduction to acoustic Helmholtz equations. Both versions of the Helmholtz equations are challenging numerically. The elastic Helmholtz equation is larger, as a system of PDEs, and harder to solve due to its more complicated physics. It was recently suggested that the elastic Helmholtz equation can be reformulated as a generalized saddle-point system, opening the door to the current development. Utilizing the approximate commutativity of the underlying differential operators, we suggest a block-triangular preconditioner whose diagonal blocks are acoustic Helmholtz operators. Thus, we enable the solution of the elastic version using virtually any existing solver for the acoustic version as a black-box. We prove a sufficient condition for the convergence of our method, that sheds light on the long questioned role of the commutator in the convergence of approximate commutator preconditioners. We show scalability of our preconditioner with respect to the Poisson ratio and with respect to the grid size. We compare our approach, combined with multigrid solve of each block, to a recent monolithic multigrid method for the elastic Helmholtz equation. The block-acoustic multigrid achieves a lower computational cost for various heterogeneous media, and a significantly lower memory consumption, compared to the monolithic approach. It results in a fast solution method for wave propagation problems in challenging heterogeneous media in 2D and 3D.

• The paper introduces a block-acoustic preconditioner that decouples the elastic Helmholtz equation into sequential acoustic solves, significantly reducing computational cost.
• The methodology leverages MAC discretization and a mixed formulation to partition elastic wave equations into acoustically solvable blocks, ensuring scalability.
• Numerical benchmarks on SEG/EAGE and Overthrust models demonstrate improved convergence, memory efficiency, and robust performance in heterogeneous media.

Block-Acoustic Preconditioning for the Elastic Helmholtz Equation

Introduction

The elastic Helmholtz equation underpins frequency-domain wave modeling in solid media and is fundamental for forward modeling in seismic inversion. Unlike its acoustic counterpart, the elastic Helmholtz equation presents significant numerical challenges: it forms a strongly indefinite, high-dimensional, and coupled linear system due to pressure and shear wave physics, and its discretization on fine meshes for high-frequency propagation produces large-scale matrix systems. Despite the proliferation of efficient solvers for acoustic Helmholtz problems, analogous approaches for the elastic version are limited, with prevailing methods reliant on costly monolithic multigrid iterations. This work introduces a robust block-acoustic preconditioner for the elastic Helmholtz equation, leveraging operator commutativity to permit scalable, memory-efficient solutions by reducing the elastic problem to a sequence of acoustic Helmholtz solves.

Mathematical Foundation and Preconditioner Derivation

The elastic Helmholtz equation for isotropic, frequency-domain modeling is typically written as:

$$\lambda \nabla(\nabla \cdot \mathbf{u}) + \mu \nabla^2 \mathbf{u} + \rho \omega^2 \left( 1 - \frac{\gamma}{\omega}\right) \mathbf{u} = \mathbf{q}_s,$$

where $\mathbf{u}$ denotes the displacement, $\lambda$ and $\mu$ are Lamé parameters, $\rho$ is density, $\omega$ the angular frequency, and $\gamma$ denotes attenuation.

The key innovation is the exploitation of a mixed formulation, where the equation is recast as a generalized saddle-point system. The discretization is performed with a MAC (Marker-and-Cell) scheme, where displacement components are stored at cell faces and pressure (as a Lagrangian multiplier) at cell centers.

Figure 1: A MAC discretization cell in 3D shows variable stencils for displacement and pressure fields.

This structure naturally partitions the discretized operator into blocks, where each diagonal entry corresponds to an acoustic Helmholtz operator. Specifically, the block structure can be leveraged to formulate a block lower-triangular preconditioner, with diagonal blocks corresponding to acoustic Helmholtz problems with either shear or pressure wave speeds.

The preconditioner then has the form:

$$\mathcal{P} = \begin{pmatrix} A & B^T \ 0 & H_p \end{pmatrix},$$

where $A$ is block-diagonal (acoustic Helmholtz for shears), $B$ stems from discretized divergence/gradient, and $H_p$ is an acoustic Helmholtz operator in the pressure space.

This construction directly enables the use of state-of-the-art acoustic Helmholtz solvers for each diagonal block, effectively decoupling the elastic system and reducing overall solution cost.

Convergence Analysis and Role of the Commutator

A novel aspect of this work is the rigorous theoretical analysis of preconditioner convergence in highly indefinite, block-saddle systems. The authors establish that the norm of the operator commutator alone does not reliably predict convergence: even for small commutators, the preconditioned Krylov method can diverge due to the influence of high frequency or low attenuation regimes.

A sufficient condition for convergence is introduced, hinging not just on the commutator norm $\|\Xi\|$, but on the spectral radius $\rho(Z)$ of

$Z = \Xi A^{-1} B^T H_p^{-1}$

with $\Xi$ the commutator. The result generalizes commutator-based block preconditioning theory to indefinite, non-SPD saddle problems, clarifying control parameters and providing analytical evidence for the need of complex (attenuation) shifts in high-contrast and highly heterogeneous settings.

Multigrid Acceleration and Practical Implementation

The block-acoustic preconditioner is designed to be solver-agnostic for each diagonal block. The authors employ a complex-shifted Laplacian multigrid (CSLP) method on each Helmholtz block, adjusted for optimal performance vis-à-vis discretization and problem regularity. Compared to monolithic multigrid for the full elastic system, this decoupled approach yields a dramatic reduction in per-cycle memory consumption and computational FLOPs, especially as system size and dimension increase.

Experiments demonstrate that in challenging, geologically heterogeneous media, the block-acoustic multigrid method attains equal or better iteration counts relative to monolithic Vanka-type multigrid and maintains significantly lower total computation due to reduced coarse-grid fill-in and natural parallelism in the block structure. This scalability holds especially with increasing Poisson ratios and grid sizes, a property previously unattained in existing solvers.

Numerical Benchmarks in Heterogeneous Media

The authors provide a comprehensive set of experiments in both 2D and 3D. On elastic extensions of the SEG/EAGE salt and Marmousi2 models, the block-acoustic preconditioner achieves rapid convergence with modest or zero shift, outperforming direct monolithic approaches in both iteration count and total operation cost.

Figure 2: The SEG/EAGE salt model presents a challenging, high-contrast elasticity benchmark for preconditioned solvers.

For volumetrically large 3D cases such as the Overthrust model, the proposed method solves systems with tens of millions of unknowns using standard workstation memory budgets, benefiting from block decomposition and parallelism.

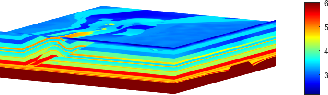
Figure 3: The Overthrust model, showing pressure wave velocity heterogeneity representative of real-world subsurface imaging tasks.

Empirically, convergence is robust with respect to material jumping coefficients and scaling in discretization density, and the memory savings from block-diagonalization are substantial. Notably, the solution of each acoustic block may utilize any existing state-of-the-art acoustic preconditioner as a black-box, future-proofing the method as those solvers improve.

Implications and Future Directions

This work establishes commutator-based block preconditioners as a viable, scalable class for saddle systems arising in frequency-domain elastodynamics. The key implication is a generic framework: scalable acoustic solvers can be lifted to the elastic regime without re-engineering, provided care is taken with operator commutativity and saddle structure.

Additionally, the rigorous spectral analysis provides tools for predicting and mitigating divergence in high-frequency, low-attenuation scenarios. This formalism readily extends to other coupled PDE systems where indefinite blocks and non-trivial commutators are present.

From a practical geophysical perspective, the methodology enables full-waveform inversion and large-scale simulation with moderate hardware requirements. Block preconditioning also aligns with current trends in high-performance computing, favoring parallelism and memory efficiency.

Looking forward, advances in scalable acoustic Helmholtz solvers—especially those leveraging learning-based or algebraic multigrid acceleration—can be directly incorporated into the block-acoustic preconditioning paradigm for elasticity. Additional investigation into adaptive shifts in heterogeneous and anisotropic materials and the extension to unstructured meshes is of clear interest.

Conclusion

The paper presents a methodologically robust and computationally efficient framework for elastic Helmholtz solutions, advancing preconditioning theory for indefinite, coupled wave systems (2411.15897). The block-acoustic preconditioner exhibits strong scalability, memory savings, and empirical efficiency in heterogeneous, large-scale geophysical models, providing a template for future solver development and broader application to coupled PDEs.