Computable Lipschitz Bounds for Deep Neural Networks (2410.21053v1)

Abstract: Deriving sharp and computable upper bounds of the Lipschitz constant of deep neural networks is crucial to formally guarantee the robustness of neural-network based models. We analyse three existing upper bounds written for the $l^2$ norm. We highlight the importance of working with the $l^1$ and $l^\infty$ norms and we propose two novel bounds for both feed-forward fully-connected neural networks and convolutional neural networks. We treat the technical difficulties related to convolutional neural networks with two different methods, called explicit and implicit. Several numerical tests empirically confirm the theoretical results, help to quantify the relationship between the presented bounds and establish the better accuracy of the new bounds. Four numerical tests are studied: two where the output is derived from an analytical closed form are proposed; another one with random matrices; and the last one for convolutional neural networks trained on the MNIST dataset. We observe that one of our bound is optimal in the sense that it is exact for the first test with the simplest analytical form and it is better than other bounds for the other tests.

• The paper introduces novel computable bounds, K3 and K4, that significantly tighten Lipschitz constant estimates for deep neural networks.
• It demonstrates the effectiveness of l1 and l∞ norms and extends these bounds to CNNs using both explicit and implicit max-pooling decompositions.
• Empirical results on random networks, function approximations, and MNIST CNNs confirm the benefits of the proposed bounds, especially the sharpness and reduced variance of K4.

Computable Lipschitz Bounds for Deep Neural Networks

Motivation and Problem Statement

The stability of deep neural networks (DNNs) under small input perturbations is a critical property, especially in adversarial and safety-critical contexts. The Lipschitz constant of a neural network provides a formal measure of this stability, bounding the network's sensitivity to input changes. However, existing upper bounds for the Lipschitz constant are often either loose or computationally intractable for deep architectures, particularly in the $l^2$ norm. This work systematically analyzes existing bounds, highlights the importance of $l^1$ and $l^\infty$ norms, and introduces two novel, sharper, and efficiently computable bounds for both fully-connected and convolutional neural networks (CNNs). Theoretical results are substantiated with comprehensive numerical experiments, including cases where the exact Lipschitz constant is known.

Review of Existing Lipschitz Bounds

The classical approach to bounding the Lipschitz constant of a DNN is to multiply the operator norms of the weight matrices across layers, yielding the so-called "worst-case" bound $K_*$. While this is straightforward, it is highly pessimistic and grows exponentially with network depth, rendering it ineffective for deep models. More refined bounds, such as the Combettes-Pesquet bound ($K_1$) and the Virmaux-Scaman bound ($K_2$), exploit the structure of activation functions and matrix products to provide tighter estimates. However, these bounds either remain loose in practice or are computationally expensive due to the combinatorial explosion in the number of terms.

Novel Bounds: $K_3$ and $K_4$

The paper introduces two new bounds, $K_3$ and $K_4$, specifically tailored for $l^1$ and $l^\infty$ norms. The $K_3$ bound leverages the element-wise absolute value of weight matrices, exploiting the fact that for these norms, the induced matrix norm of a product is bounded by the product of the absolute value matrices. The $K_4$ bound further refines this by combining the Combettes-Pesquet decomposition with the absolute value trick, yielding a bound that is provably sharper than both $K_1$ and $K_3$.

Theoretical analysis establishes the following hierarchy:

$L \leq K \leq K_4 \leq \min(K_1, K_3) \leq K_*,$

where $L$ is the true Lipschitz constant and $K$ is the ideal (but generally intractable) bound.

Extension to Convolutional Neural Networks

The extension of these bounds to CNNs is nontrivial due to the presence of convolutional, pooling, and activation layers. The paper develops two approaches:

• Explicit Approach: Decomposes max-pooling operations into compositions of simpler row-wise and column-wise pooling, allowing the application of the same bounding techniques as for fully-connected layers. This approach is exact but can be computationally intensive for large kernels.
• Implicit Approach: Represents max-pooling as a single linear operation with a data-dependent selection matrix, significantly reducing computational complexity at the cost of some looseness in the bound.

Both approaches yield computable analogues of $K_1$, $K_3$, and $K_4$ for CNNs, and the theoretical ordering of bounds is preserved.

Numerical Experiments

Random Networks

Empirical evaluation on randomly initialized fully-connected networks confirms the theoretical ordering of bounds. The $K_4$ bound consistently provides the tightest computable upper bound, with significantly reduced variance compared to $K_1$ and $K_3$.

Polynomial Function Approximation

The paper constructs deep ReLU networks that exactly or efficiently approximate $x^2$ and $xy$ using explicit series representations. For the $x^2$ network, the $K_4$ bound is exact for certain architectures, while $K_*$, $K_1$, and $K_2$ grow exponentially with depth. This is illustrated in the following figure:

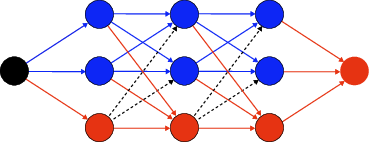
Figure 1: Graphical representation of the network representing the function $x - \sum_{r=0}^3 \frac{g_r(x)}{4^r}$.

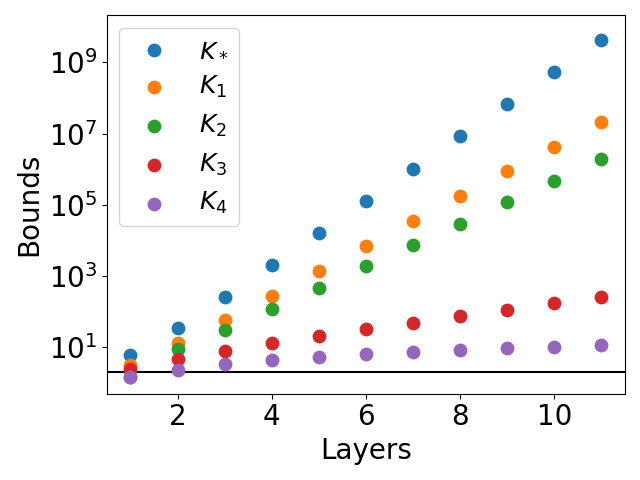
Figure 2: Lipschitz bounds for networks approximating the function $x^2$. The function $g$ is represented as in equation (6).

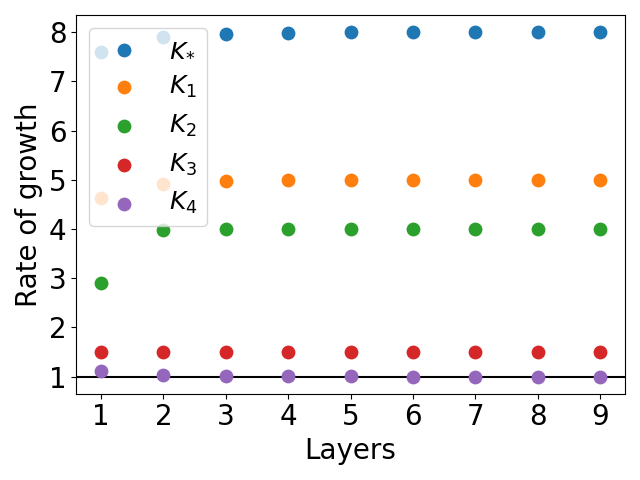
Figure 3: Rates of growth for networks approximating the function $x^2$. The function $g$ is represented as in equation (6).

For the $xy$ function, a novel mesh-based construction is proposed, and the bounds are evaluated for networks of increasing depth. All bounds except $K_4$ exhibit exponential growth, while $K_4$ remains much tighter.

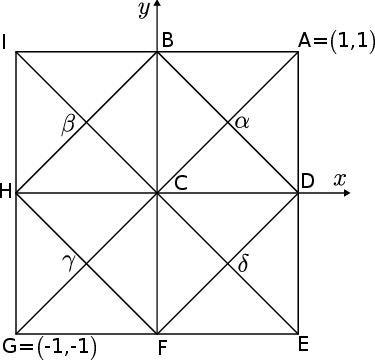
Figure 4: Mesh used to construct the neural network approximating the function $xy$ on $[-1,1]^2$.

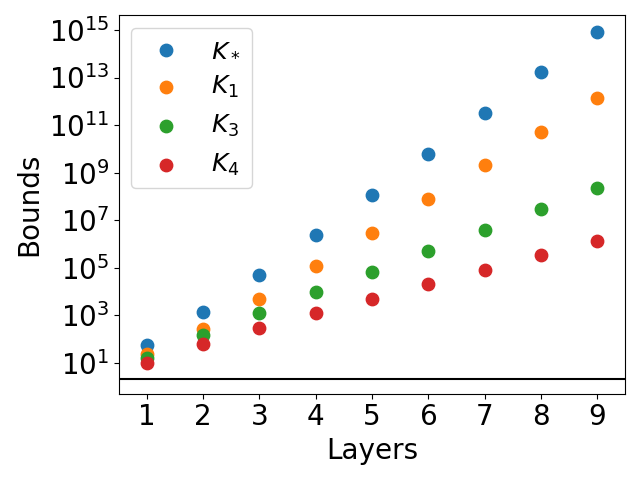
Figure 5: Lipschitz bounds for networks approximating the function $xy$. The function $\hat\varphi$ is represented as in equation (19).

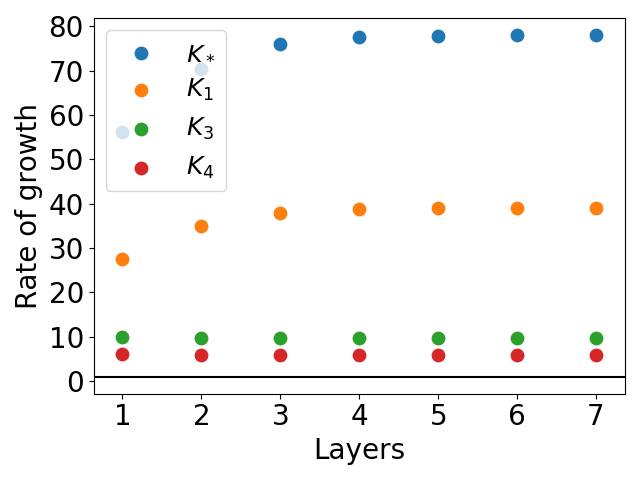
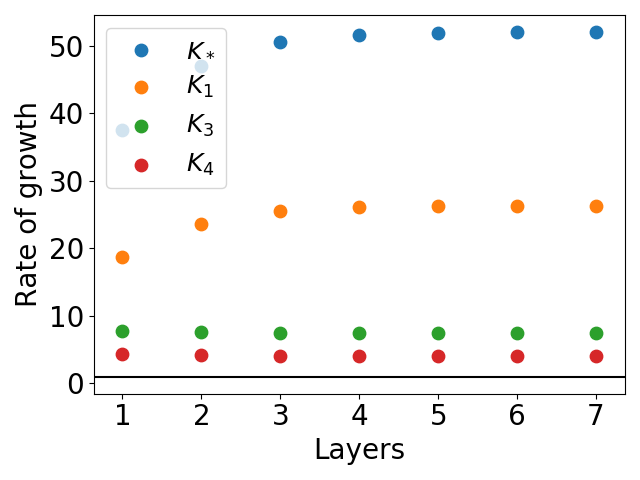
Figure 6: Rates of growth for networks approximating the function $xy$. The function $\hat\varphi$ is represented as in equation (19).

Convolutional Neural Networks on MNIST

The bounds are further tested on CNNs trained on MNIST with various architectures and regularization strengths. The $K_4$ bound, both in explicit and implicit forms, consistently outperforms other computable bounds. The implicit approach yields tighter bounds than the explicit approach, especially for large networks with multiple max-pooling layers. Increasing $l^2$ regularization during training leads to lower Lipschitz bounds, confirming the practical utility of these estimates for controlling network robustness.

Theoretical and Practical Implications

The results demonstrate that the $l^1$ and $l^\infty$ norms are preferable for certifying Lipschitz bounds in many practical scenarios, particularly for networks with ReLU or similar activations. The $K_4$ bound provides a practical tool for certifying robustness, with computational complexity comparable to existing methods but with significantly improved tightness. The explicit construction of networks approximating $x^2$ and $xy$ with known Lipschitz constants provides valuable benchmarks for future theoretical analysis.

The extension to CNNs, including both explicit and implicit approaches for max-pooling, enables the application of these bounds to state-of-the-art architectures in computer vision and scientific computing. The empirical results suggest that these bounds can be integrated into training pipelines for regularization or certification purposes.

Future Directions

Potential avenues for further research include:

• Extending the analysis to other norms and activation functions.
• Developing efficient algorithms for computing or approximating $K_4$ in very large-scale networks.
• Integrating these bounds into training objectives to directly optimize for robustness.
• Generalizing the explicit network constructions to broader classes of functions and higher dimensions.

Conclusion

This work provides a comprehensive theoretical and empirical analysis of computable Lipschitz bounds for deep neural networks, introducing two new bounds that are provably sharper than existing alternatives in $l^1$ and $l^\infty$ norms. The $K_4$ bound, in particular, is shown to be optimal in certain cases and consistently outperforms prior bounds in practical settings. The extension to CNNs and the demonstration on both synthetic and real-world tasks underscore the practical relevance of these results for robust deep learning.