- The paper introduces γ_X as a robust early warning sign that reliably indicates critical transitions across both Gaussian and non-Gaussian α-stable noise systems.
- It demonstrates through numerical simulations that classical methods based on variance and autocorrelation can yield false positives when applied to heavy-tailed α-stable processes.
- The findings offer a mathematically grounded and practical alternative for anticipating critical transitions in climate and ecological models.
Early Warning Signs in α-Stable Systems
The paper "Early warning signs of critical transitions -- The α-stable case" focuses on the limitations of classical early warning signs when applied to stochastic dynamical systems characterized by non-Gaussian, α-stable noise. It provides a generalized alternative approach by introducing the scaling factor γX as a robust early warning indicator applicable to systems driven by both Gaussian and non-Gaussian α-stable noise.
Introduction to Critical Transitions
Stochastic dynamical systems are crucial for understanding rapid and irreversible changes in ecological and climate systems. The anticipation of such critical transitions is vital, particularly for applications in climate science. Traditional statistical early warning signs such as variance and autocorrelation have been widely used to predict these transitions. However, these signs usually rely on the assumption of Gaussian noise, which may not hold for many real-world systems where α-stable distributions offer a more accurate representation due to their heavy-tailed nature.
Limitations of Classical Early Warning Signs
The paper challenges the assumption that Gaussian noise drives all dynamical systems. Systems subject to α-stable noise show divergent variance, rendering classical early warning signs potentially misleading. Specifically, the use of rising variance or autocorrelation as indicators can lead to false positives, as these statistical properties may increase even under constant environmental conditions in α-stable systems.
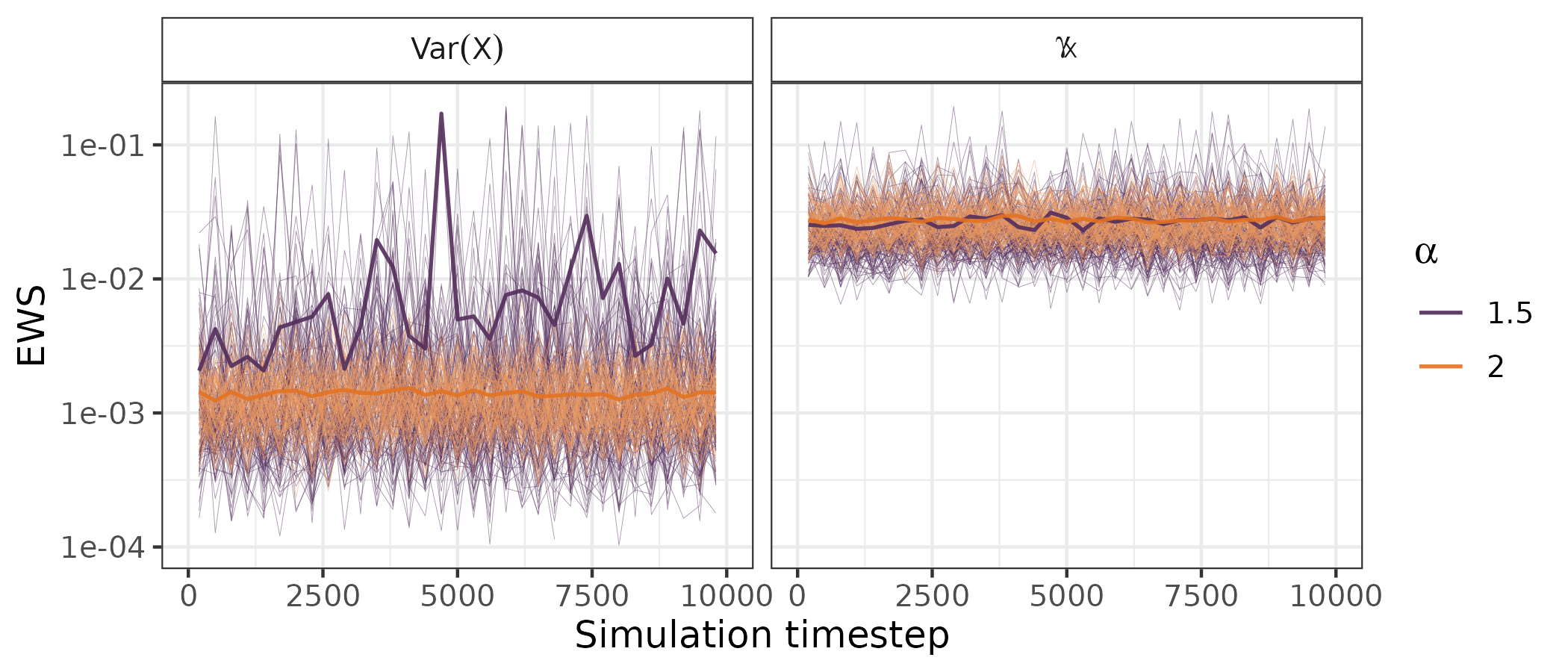
Figure 1: Illustration of non-converging variance. In the Gaussian case (alpha = 2), the variance converges to a final value once the simulation has reached equilibrium due to the central limit theorem (orange trajectories in the left panel). In the non-Gaussian, alpha-stable case, the variance of X does not converge to a finite value and may thus exhibit a spurious increase even for constant k, giving rise to a false-positive early warning sign (purple trajectories in the left panel). In contrast, gamma_X converges for all alpha (right panel). Thin lines are individually simulated trajectories, bold lines average over all 100 trajectories, k = 1. Note the log scale on the y-axis. Simulation setup mirrors Figure ~\ref{fig:gamma_neq}
Introduction of γX as a Generalized Approach
To address the shortcomings in the classical method, the paper introduces γX as a novel early warning sign. This scaling parameter, derived from the properties of α-stable processes, scales inversely with the bifurcation parameter k. Hence, γX is positioned to serve as a stable early warning sign across different noise types.
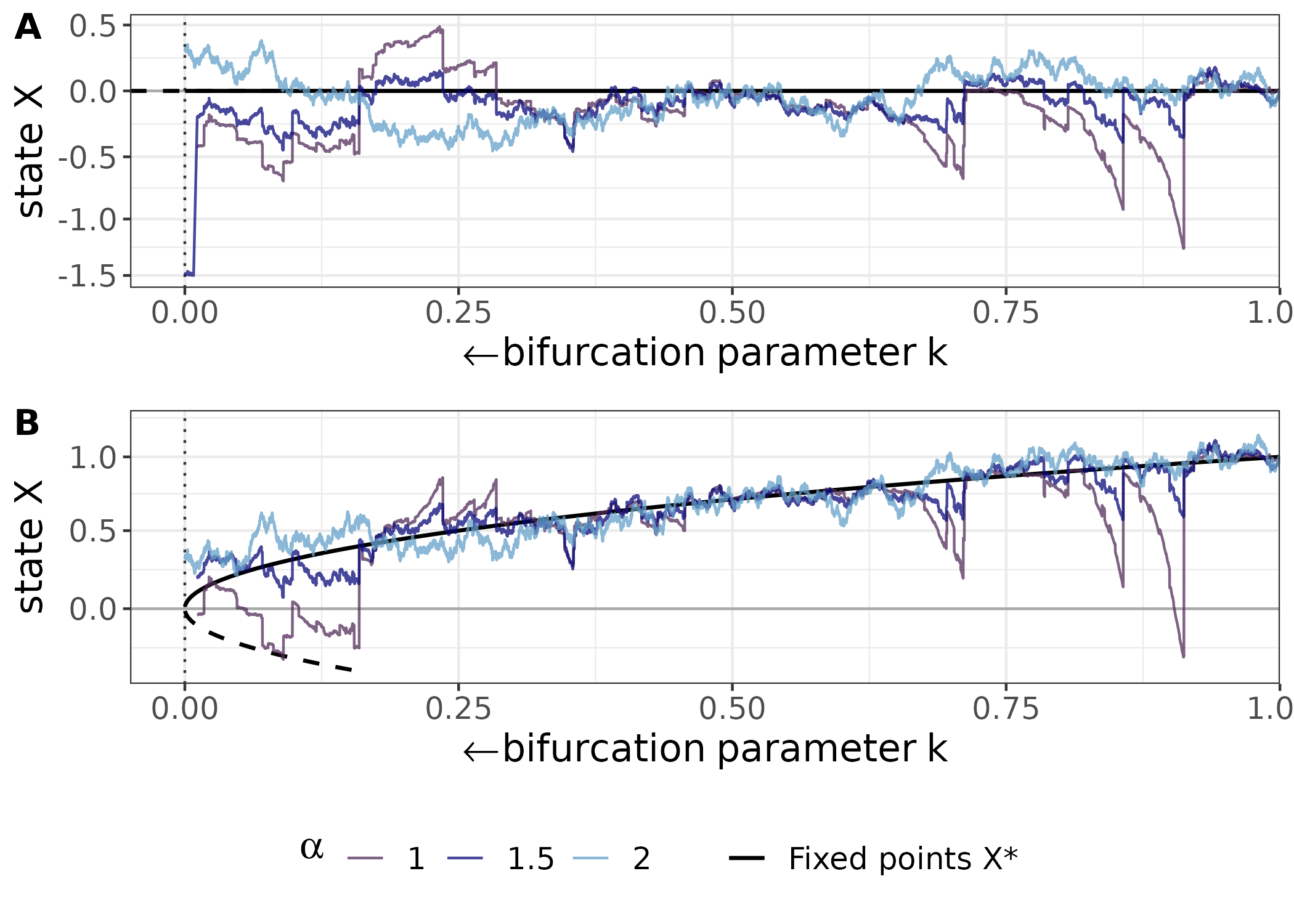
Figure 2: Bifurcation diagrams of the Ornstein-Uhlenbeck process showing stability changes at k=0.
The mathematical grounding shows that for α-stable noise, X(t) exhibits an increase in γX as the system approaches a bifurcation, parallel to the increase observed in variance for Gaussian systems.
Numerical Simulations and Applicability
The paper provides comprehensive equilibrium and non-equilibrium simulations to validate the theoretical constructs around γX. Equilibrium simulations showcase strong alignment between the estimated and theoretical values of γX, confirming its reliability as an indicator.
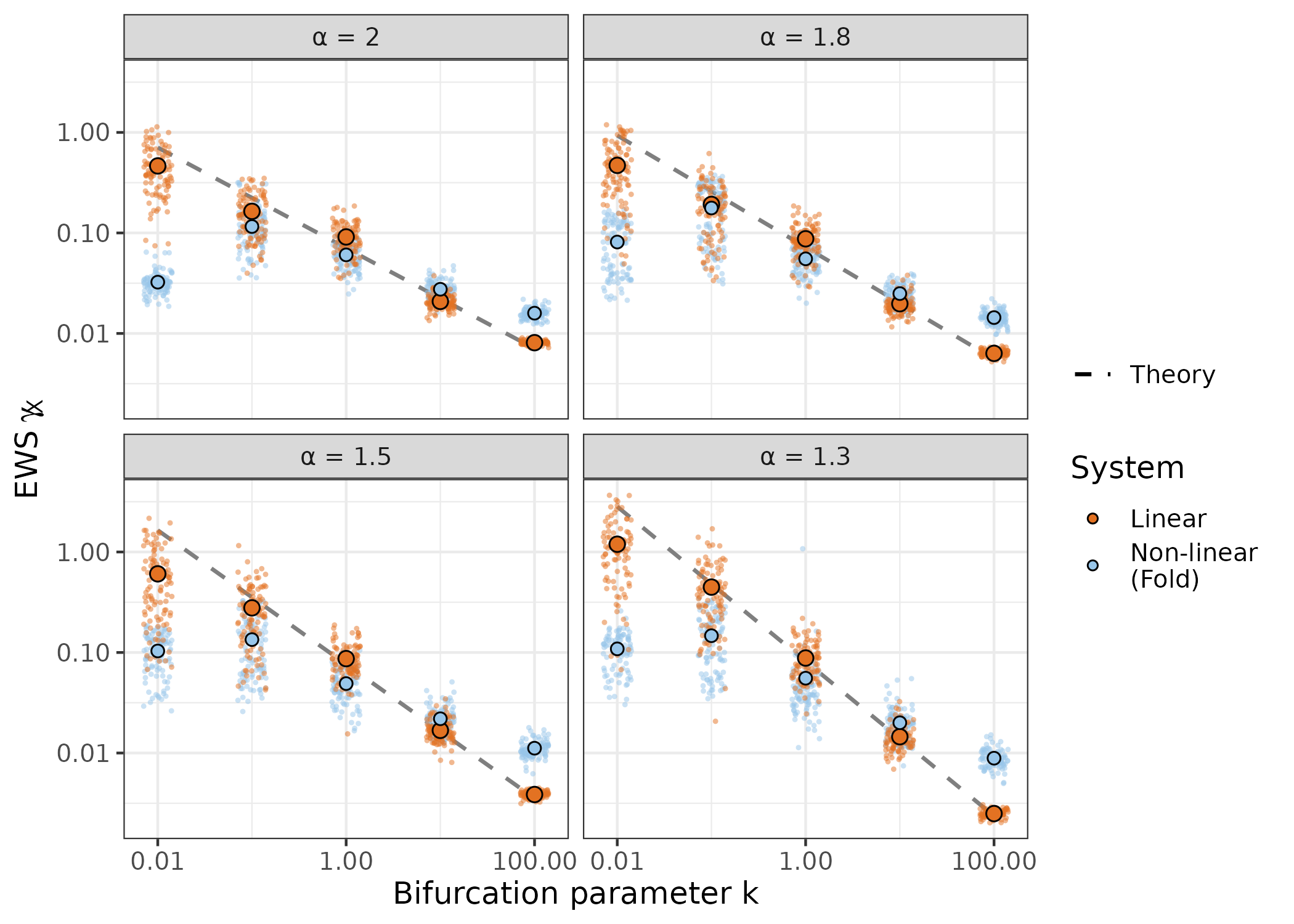
Figure 3: Equilibrium simulations: Estimation of γX for the linear and non-linear systems demonstrates conformity with theoretical predictions across different values of k.
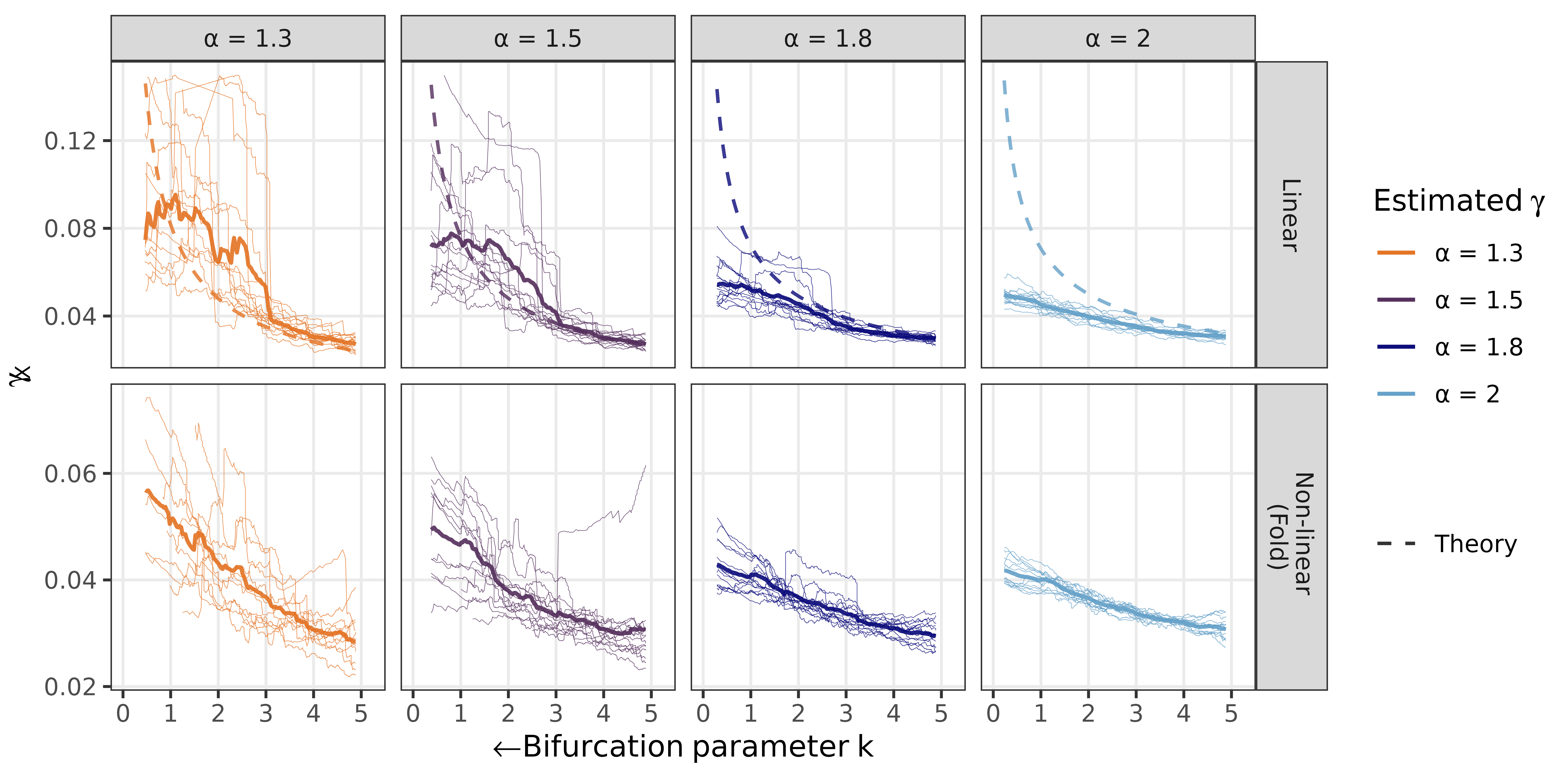
Figure 4: Non-equilibrium simulations reveal consistent behavior of γX as k approaches bifurcation, validating its practical application.
These simulations highlight the potential for γX to be used in real-world applications, especially where data is limited, offering a reliable alternative to traditional early warning signs.
Conclusion
The research posits that the classical early warning signs fail to account for systems driven by α-stable noise, while γX provides a mathematically grounded and practically applicable alternative. It affirms that γX increases predictably with decreasing bifurcation parameter k, offering a viable indicator of impending critical transitions in non-Gaussian systems. By leveraging the α-stable distribution characteristics, the findings pave the way for more reliable predictions in climate science and ecological systems, where heavy-tailed distributions are prevalent.



