Ternary and Binary Quantization for Improved Classification (2203.16798v1)

Abstract: Dimension reduction and data quantization are two important methods for reducing data complexity. In the paper, we study the methodology of first reducing data dimension by random projection and then quantizing the projections to ternary or binary codes, which has been widely applied in classification. Usually, the quantization will seriously degrade the accuracy of classification due to high quantization errors. Interestingly, however, we observe that the quantization could provide comparable and often superior accuracy, as the data to be quantized are sparse features generated with common filters. Furthermore, this quantization property could be maintained in the random projections of sparse features, if both the features and random projection matrices are sufficiently sparse. By conducting extensive experiments, we validate and analyze this intriguing property.

• The paper presents a pipeline using sparse random projections followed by quantization to boost classification accuracy and efficiency.
• The paper details how ternary and binary quantization minimizes noise in sparse feature representations while preserving essential data characteristics.
• The paper demonstrates that the proposed kNEC classifier robustly handles outliers and noise, achieving competitive performance on large-scale datasets.

Ternary and Binary Quantization for Improved Classification

Introduction

The paper "Ternary and Binary Quantization for Improved Classification" investigates the use of ternary and binary quantization techniques on sparse feature representations to enhance classification accuracy in large-scale datasets. The methodology involves an initial dimension reduction via random projection followed by quantization into binary or ternary codes. This sequence is intended to tackle the challenges posed by large data storage needs and computational demands in object classification tasks.

Methodology

Sparse Feature Generation

The generation of sparse features is a critical step in the proposed pipeline. The authors emphasize using feature generators that suit the complexity of the dataset. For simpler datasets such as YaleB, linear filters like DWT and DCT are sufficient, while more complex datasets like CIFAR-10 and ImageNet require sophisticated filters such as deep CNNs. These filters generate sparse feature representations of data, often exhibiting heavy-tailed symmetric distributions, as depicted in the frequency histograms for YaleB, CIFAR-10, and ImageNet.

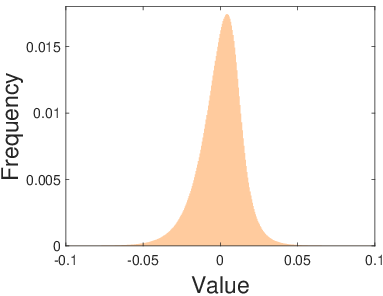
Figure 1: The frequency histograms of the sparse features of YaleB, CIFAR-10, and ImageNet, demonstrating heavy-tailed symmetric distributions generated by DCT, AlexNet Conv5, and VGG16 Conv5_3, respectively.

Random Projection with Sparse Matrices

A key component of the approach is the generation of sparse projections through random projection matrices. Sparse ternary matrices are preferred for their ability to maintain sparsity and achieve quantization gains when used with sparse features. Specifically, $\{0, \pm 1\}$-matrices with one nonzero element per column are suggested. This choice contrasts with Gaussian random matrices that tend to produce dense projections, unsuitable for reaping the benefits of ternary or binary quantization.

Quantization Process

Quantization is performed by converting sparse feature vectors to ternary codes, followed by further reduction to binary codes. The process involves zeroing elements below a specified threshold and unifying the magnitude of significant elements. The ternary coding is designed to exploit the nature of sparse feature distributions—common in frequency/spatial domains—resulting in minimal accuracy loss while potentially enhancing classification due to removal of noise and edge gradients.

Exemplar-Based Classification

The authors propose a $k$-nearest exemplar-based classifier ($k$NEC) that measures class similarity by summing the distances to $k$ nearest exemplars within that class. This approach achieves a favorable balance between the computational simplicity of $k$NN and the performance of LSC by addressing noise and outlier sensitivity effectively.

Experimental Results

The experiments validate the proposed method's performance over three benchmark datasets: YaleB, CIFAR-10, and ImageNet. The classification efficacy is assessed by comparing real-valued codes (RC) against ternary (TC) and binary codes (BC) across various sparsity ratios. Notably, $k$NEC delivers superior performance over $k$NN and comparable results to LSC, supporting the claim that sparse feature projections maintain quantization gains under the discussed pipeline.

Conclusion

This paper highlights the potential of ternary and binary quantization in maintaining, or even improving, classification accuracy when applied to sparse features and their sparse random projections. The proposed $k$NEC classifier serves as an efficient method that leverages sparsity in data, exhibiting robustness against noise and outliers. The results suggest that using sufficiently sparse matrices for random projection is more beneficial than traditional dense Gaussian matrices. Future research could explore broader applications of the quantization technique in AI, particularly in enhancing real-time performance in classification tasks and reducing resource consumption in large-scale machine learning models.