Nearest Class-Center Simplification through Intermediate Layers

Abstract: Recent advances in theoretical Deep Learning have introduced geometric properties that occur during training, past the Interpolation Threshold -- where the training error reaches zero. We inquire into the phenomena coined Neural Collapse in the intermediate layers of the networks, and emphasize the innerworkings of Nearest Class-Center Mismatch inside the deepnet. We further show that these processes occur both in vision and LLM architectures. Lastly, we propose a Stochastic Variability-Simplification Loss (SVSL) that encourages better geometrical features in intermediate layers, and improves both train metrics and generalization.

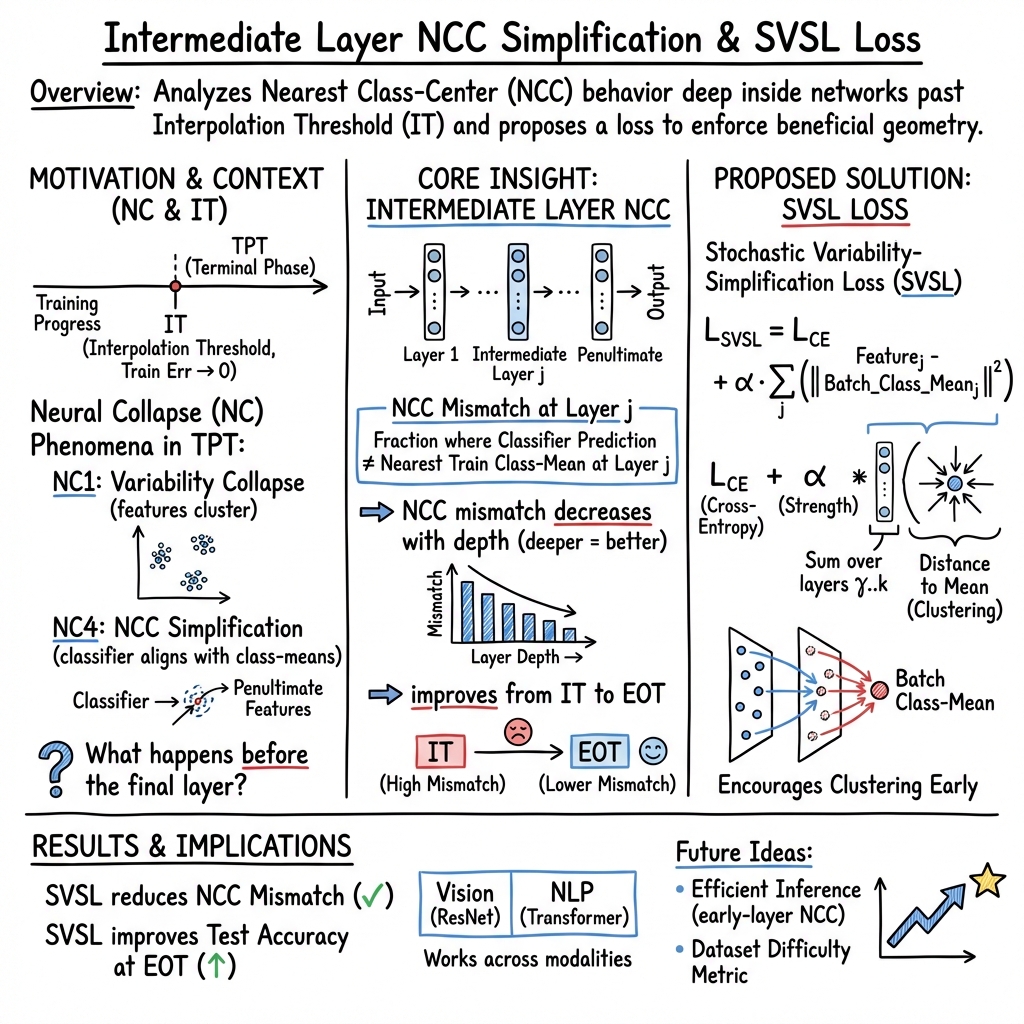
• The paper introduces SVSL, a novel loss that minimizes NCC mismatch across intermediate layers, leading to enhanced class clustering and geometric alignment.
• The methodology leverages intermediate layer representations to analyze Neural Collapse, demonstrating superior performance on datasets such as MNIST and CIFAR10.
• The findings imply that incorporating geometric insights into neural network training can improve both training efficiency and generalization in vision and NLP tasks.

Nearest Class-Center Simplification through Intermediate Layers

Introduction

This paper introduces and investigates Nearest Class-Center (NCC) Simplification through intermediate layers of neural networks, expanding the concept of Neural Collapse as described in prior research. The authors present a novel loss function, the Stochastic Variability-Simplification Loss (SVSL), that encourages better geometric characteristics in intermediate layers and improves both training metrics and generalization across various tasks, including vision and NLP sequence classification.

Neural Collapse in Intermediate Layers

Neural Collapse describes phenomena observed past the Interpolation Threshold (IT), where the training error reaches zero. This study explores the simplification of deepnet activations to their nearest class centers, focusing on intermediate network layers. The paper establishes that during the Terminal Phase of Training (TPT), there is a structured geometric form where deeper layers exhibit lower NCC mismatch, and this behavior propagates through several layers beyond the final one.

Figure 1: STL-10 experiment training procedure. We show the accuracy on both the train and test set, using the different losses: Vanilla Cross-Entropy (Pink) and SVSL (Blue). The SVSL loss outperforms the vanilla in both metrics.

Stochastic Variability-Simplification Loss

The SVSL is introduced to reduce NCC mismatch across intermediate layers, promoting class clustering and thus enhancing the alignment between nearest class-centers and the classifier. By optimizing NCC mismatch, the SVSL improves not only train metrics but also test performance across multiple epochs, particularly within the TPT.

Figure 2: NCC Mismatch for Vision datasets: MNIST, Fashion-MNIST, and CIFAR10, using both vanilla (solid) and SVSL (dashed) losses.

Results and Implications

The empirical results across various datasets show that the SVSL consistently outperforms traditional Cross-Entropy loss at multiple stages of training, specifically at IT, EOT, and at the best test epochs. The method demonstrates superior test performance, reaching optimal results during the TPT for most datasets.

Figure 3: Optimization Procedures for Vision experiments: MNIST, Fashion-MNIST, CIFAR10, CIFAR100. The SVSL achieves higher performance(test and train) at most epochs.

Practical and Theoretical Implications

The exploration into intermediate layer geometries and NCC mismatch provides insights into neural network training dynamics, suggesting potential pathways for enhancing model performance. The findings support the notion that leveraging geometric properties in neural networks can be beneficial for both training efficiency and generalization capabilities. Future work may explore integrating SVSL into automated hyperparameter tuning processes or further investigate NCC behaviors in diverse architectures and tasks.

Conclusion

This study extends the understanding of NCC simplification in deep networks and introduces the SVSL as a powerful tool for improving neural network performance. The demonstrated benefits across various tasks underscore the potential of integrating geometric insights into neural network training strategies, offering a promising avenue for future research and practical application enhancements.