Learning to Give Checkable Answers with Prover-Verifier Games (2108.12099v1)

Abstract: Our ability to know when to trust the decisions made by machine learning systems has not kept up with the staggering improvements in their performance, limiting their applicability in high-stakes domains. We introduce Prover-Verifier Games (PVGs), a game-theoretic framework to encourage learning agents to solve decision problems in a verifiable manner. The PVG consists of two learners with competing objectives: a trusted verifier network tries to choose the correct answer, and a more powerful but untrusted prover network attempts to persuade the verifier of a particular answer, regardless of its correctness. The goal is for a reliable justification protocol to emerge from this game. We analyze variants of the framework, including simultaneous and sequential games, and narrow the space down to a subset of games which provably have the desired equilibria. We develop instantiations of the PVG for two algorithmic tasks, and show that in practice, the verifier learns a robust decision rule that is able to receive useful and reliable information from an untrusted prover. Importantly, the protocol still works even when the verifier is frozen and the prover's messages are directly optimized to convince the verifier.

• The paper presents a game-theoretic framework where a prover and a verifier interact to ensure checkable AI decision outputs.
• It details verifier-first strategies and equilibrium analyses to achieve sound and complete verification protocols under adversarial conditions.
• Empirical results, including the FindThePlus experiment, demonstrate high precision and robustness in extracting verifiable identifiers.

Learning to Give Checkable Answers with Prover-Verifier Games

Introduction to Prover-Verifier Games

Prover-Verifier Games (PVGs) represent a novel game-theoretic framework aimed at ensuring machine learning systems make verifiable decisions. They are particularly applicable in contexts where the reliability and trustworthiness of automated decisions are paramount, such as high-stakes environments subject to adversarial attacks. The framework involves two players: a powerful but potentially deceptive prover and a trustworthy verifier, albeit with limited computational resources. The interplay between these agents is designed to yield protocols that enhance the credibility of outputs via rigorous verification mechanisms.

Theoretical Underpinnings

The PVG is deeply inspired by concepts from computational complexity such as interactive proofs, where soundness and completeness are critical. To achieve desirable game equilibria, the verifier is programmed to seek the correct decision, while the prover's task is to convince the verifier of a particular outcome, pursuing adversarial objectives that inherently test the verifier's robustness. Vital to the successful implementation of PVG is the choice of equilibrium concepts—namely Nash and Stackelberg equilibria.

Game Formulations and Equilibrium Analysis

The research articulates several formulations of PVGs, categorized by the order in which game elements (players' strategies and problem instances) are revealed. The paper finds that verifier-first strategies, where the verifier acts before the prover with insights into problem instances post-strategy formulation, satisfy soundness and completeness, a property not uniformly seen across all PVG instantiations.

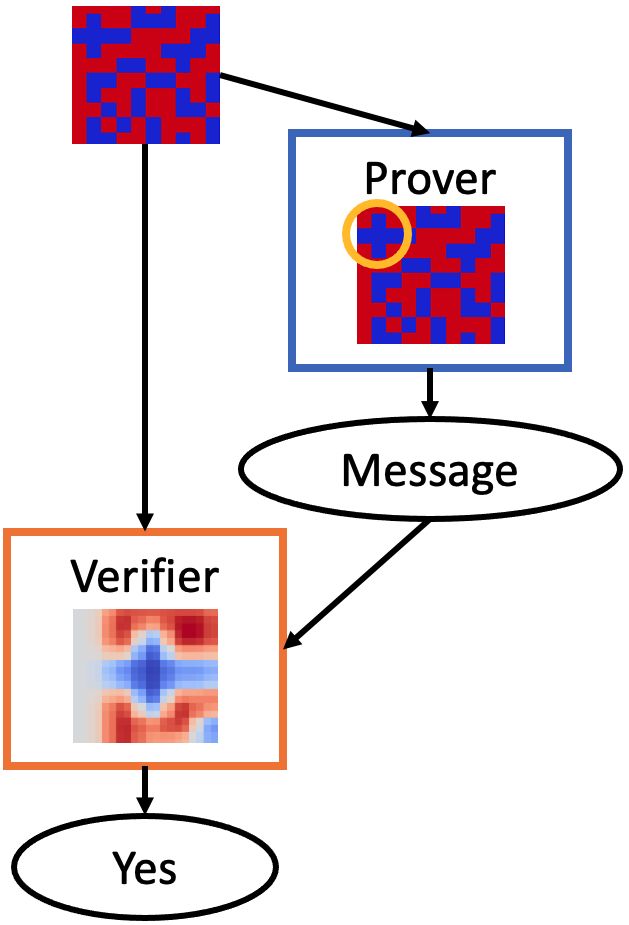
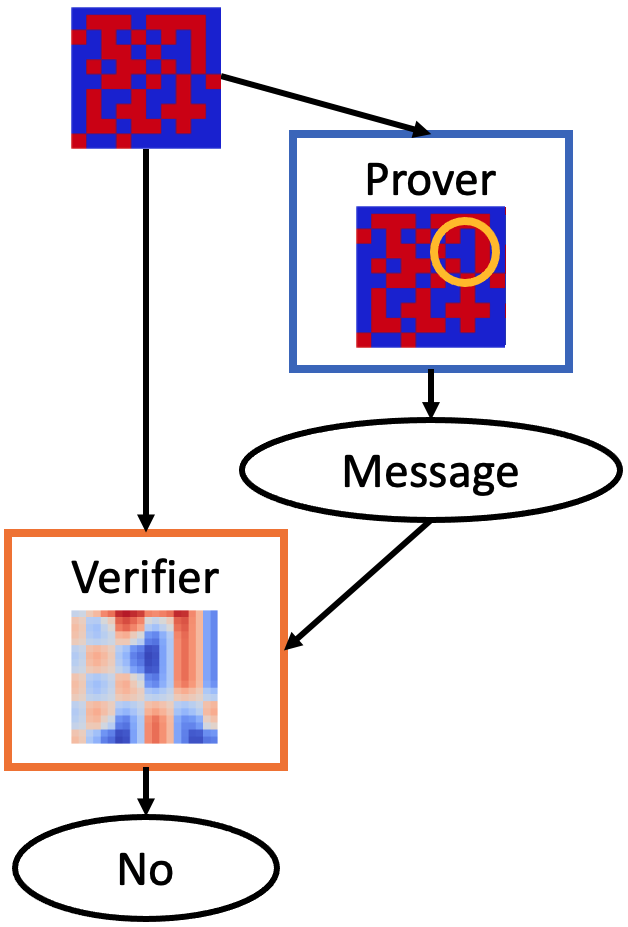
Figure 1: Pattern to detect.

A formalization is provided demonstrating that such protocols need to ensure no trivial verifiers can emerge—a situation where verifiers, absent proper strategy, default to identity functions which inherently degrade the system's reliability. Only formulations with post-strategy revelation of instances avoid this pitfall and authentically thrive within the verifier-leading sequential setup.

Finding Equilibria

The PVG approach benefits from learning dynamics borrowed from multi-agent systems such as Generative Adversarial Networks, where gradient-based optimization for Nash equilibria illustrates practical convergence strategies. Analyses on simple tasks such as the Binary Erasure Channel validated through empirical proof against collaborative baselines, verify the robustness and soundness of the protocols trained under PVG conditions.

Figure 2: FindThePlus Verifier Architecture: A schematic diagram of a single head of the Spatial Transformer Network-like verifier architecture we used in out FindThePlus experiments.

Experimental Results

The practical utility of PVGs was tested through simulations on algorithmic tasks emphasizing decision verification. Notable is the "FindThePlus" experiment where input images containing distinct patterns necessitated verifiable identifier extraction. By using architectures such as Spatial Transform Networks, the research demonstrates verifiers reliably extracting proofs from images, confirmed through metrics like high precision upon freezing the verifier and subsequently optimizing the prover and the message vectors. 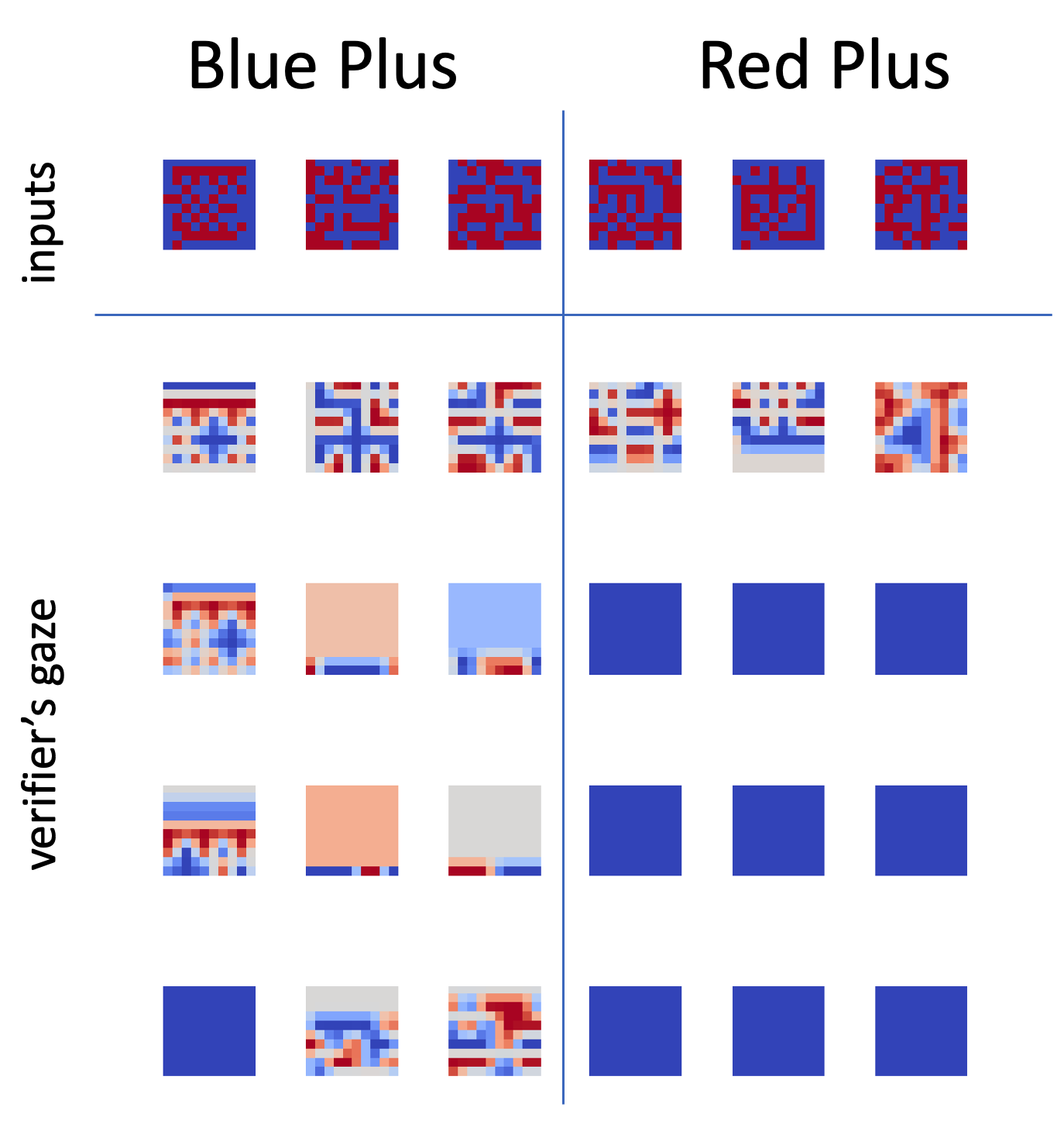*Figure 3: Visualizing Verifier's Gaze: The verifier learns spatial attentiveness, ensuring proof-location consistency within images with provers suggesting verification-worthy sections."

Conclusion

The research into Prover-Verifier Games showcases a promising avenue for verifiable decision-making protocols in AI, primarily aiding domains requiring stringent checks on automated outputs. PVGs are adept at confirming accurate outcomes in adversarial settings–ensuring both theoretical soundness and empirical success across evaluated tasks. Future research pathways include scaling these frameworks to more diverse and intricate challenge landscapes, perhaps illuminating new pathways for leveraging unverifiable but powerful agents to facilitate machine learning interpretability and trust.

This approach illustrates a pivot in developing AI systems not only capable of leveraging advanced learning techniques but intrinsically equipped to rationalize their decisions to human overseers, ensuring integrity and accountability.