The Pair-Instability Mass Gap for Black Holes

Abstract: Stellar evolution theory predicts a "gap" in the black hole birth function caused by the pair instability. Presupernova stars that have a core mass below some limiting value, Mlo, after all pulsational activity is finished, collapse to black holes, whereas more massive ones, up to some limiting value, Mhi, explode, promptly and completely, as pair-instability supernovae. Previous work has suggested Mlo is approximately 50 solar masses and Mhi is approximately 130 solar masses. These calculations have been challenged by recent LIGO observations that show many black holes merging with individual masses, Mlo is least some 65 solar masses. Here we explore four factors affecting the theoretical estimates for the boundaries of this mass gap: nuclear reaction rates, evolution in detached binaries, rotation, and hyper-Eddington accretion after black hole birth. Current uncertainties in reaction rates by themselves allow Mlo to rise to 64 solar masses and Mhi as large as 161 solar masses. Rapid rotation could further increase Mlo to about 70 solar masses, depending on the treatment of magnetic torques. Evolution in detached binaries and super-Eddington accretion can, with great uncertainty, increase Mlo still further. Dimensionless Kerr parameters close to unity are allowed for the more massive black holes produced in close binaries, though they are generally smaller.

• The paper demonstrates that key nuclear reactions and stellar dynamics significantly alter the predicted mass boundaries of the pair-instability gap for black holes.
• It employs the Kepler code to model effects of reaction rate uncertainties, rotation, and envelope retention, revealing mass shifts up to 11% in black hole formation.
• The study highlights that binary interactions and super-Eddington accretion can further modify the gap, providing insights into gravitational wave observations.

Theoretical and Computational Analysis of the Pair-Instability Mass Gap for Black Holes

Introduction

This paper presents a comprehensive investigation into the physical mechanisms and uncertainties that define the pair-instability mass gap for black holes, focusing on the lower and upper mass boundaries for black hole formation in massive stars. The study is motivated by recent gravitational wave detections of merging black holes with masses that challenge previous theoretical predictions of a mass gap between approximately $50\,M_\odot$ and $130\,M_\odot$. The authors systematically analyze four key factors: nuclear reaction rates, binary evolution, stellar rotation, and post-formation accretion, using the Kepler code for stellar evolution modeling. The implications of these factors are evaluated in the context of both single and binary star systems, with particular attention to the sensitivity of the mass gap boundaries to physical and computational uncertainties.

Nuclear Reaction Rate Uncertainties

The lower boundary of the pair-instability mass gap is highly sensitive to the rates of the $^{12}$C($\alpha,\gamma)^{16}$O and triple-alpha ($3\alpha$) reactions. The authors explore a range of experimentally motivated $S$-factors for $^{12}$C($\alpha,\gamma)^{16}$O (110–205 keV b) and a 35% upward revision for the $3\alpha$ rate, consistent with recent measurements. The ratio of these rates critically determines the central carbon abundance at helium depletion, which in turn affects the strength of the pair instability and the final black hole mass.

For non-rotating helium stars, the maximum black hole mass below the gap ($M_{\rm BH, max}$) increases from $46\,M_\odot$ (standard rates) to $64\,M_\odot$ for the most extreme rate modifications considered. However, such modifications may conflict with nucleosynthetic constraints, as large carbon abundances can suppress the pair instability and alter the yields of intermediate-mass isotopes. The upper boundary of the gap ($M_{\rm BH, min}$ above the gap) is similarly affected, with values ranging from $136\,M_\odot$ to $161\,M_\odot$ depending on the reaction rates and convective mixing assumptions.

Binary Evolution and Envelope Retention

The retention of the hydrogen envelope in single or wide binary stars allows for the formation of more massive black holes, as the envelope participates in the collapse. For low metallicity stars with reduced mass loss rates, the authors demonstrate that black holes with masses up to $90\,M_\odot$ are possible, provided the pair instability is sufficiently suppressed by high carbon abundance. However, the likelihood of such systems merging within a Hubble time is limited by the difficulty of bringing wide binaries together via gravitational radiation, and by uncertainties in mass loss mechanisms for luminous blue variables and supergiants.

Rotational Effects and Angular Momentum Transport

Stellar rotation weakens the pair instability by reducing the effective adiabatic index ($\Gamma_1$), particularly in regions of high differential rotation. The authors implement centrifugal support and angular momentum transport (including magnetic torques) in their models, finding that rapid rotation can increase $M_{\rm BH, max}$ by up to 11% compared to non-rotating cases, with the most massive black holes reaching $73\,M_\odot$ (though these may have excessive spin for direct collapse). The dimensionless Kerr parameter ($a/M$) for these remnants can approach unity, especially in models with inefficient angular momentum transport, raising the possibility of disk formation and jet-driven mass ejection during collapse.

Figure 1: Distribution of angular velocity and adiabatic index inside two $62\,M_\odot$ models at key evolutionary epochs, illustrating the impact of rotation on the pair instability criterion.

Magnetic torques play a critical role in redistributing angular momentum during long interpulse periods, with their inclusion leading to significant spin-down of the core and more realistic black hole spin parameters. The authors caution that the treatment of magnetic torques remains a major source of uncertainty, and that multi-dimensional effects may further complicate the collapse dynamics.

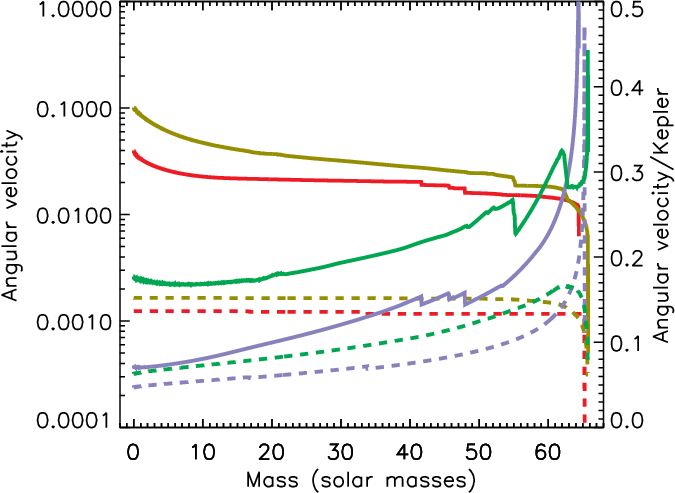
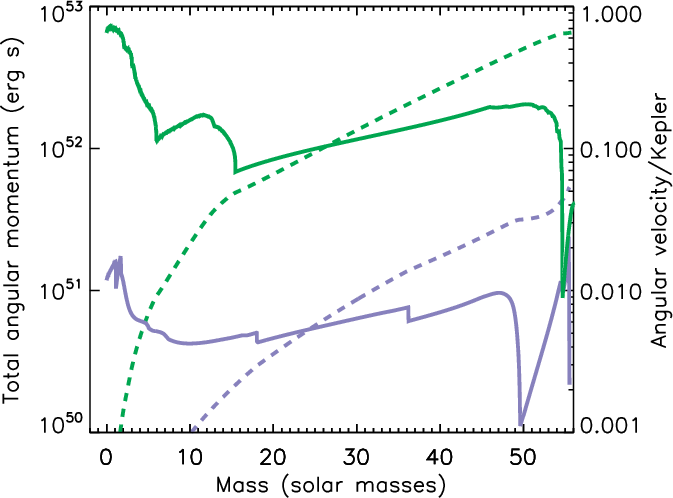
Figure 2: The effect of magnetic torques on the angular momentum distribution in a $66\,M_\odot$ model, showing substantial reduction in core angular momentum when torques are included.

Super-Eddington Accretion in Binaries

Post-formation accretion onto black holes in close binaries, particularly during common envelope or frictionally-driven mass loss phases, can further increase black hole masses beyond the pair-instability limit. The authors present toy models in which accretion rates of $10^{-3}$–$10^{-2}\,M_\odot\,{\rm yr}^{-1}$ are plausible, potentially allowing black holes to grow by $15\,M_\odot$ or more. However, the efficiency of mass retention and the frequency of such events are highly uncertain, and may be limited by the dynamics of envelope ejection and the formation of ultra-luminous X-ray sources.

Computational Methodology and Model Sensitivity

All models are computed using the Kepler code, with detailed treatment of convection, nuclear networks, and angular momentum transport. The authors emphasize the sensitivity of remnant masses to zoning, timestep criteria, and network size, particularly near the transition between collapse and explosion. The uncertainty in $M_{\rm BH, max}$ is estimated to be $\pm2\,M_\odot$ for a given set of physical assumptions. The use of pure carbon-oxygen cores as proxies for helium stars is justified for cases with high carbon abundance, as the effects of neon and helium shells are subdominant.

Implications and Future Directions

The results indicate that the pair-instability mass gap is not a strict exclusion zone, but rather a region whose boundaries are subject to significant physical and computational uncertainties. The lower boundary can be raised to $60$–$70\,M_\odot$ by plausible modifications to reaction rates and rotational effects, but reaching $85\,M_\odot$ requires either envelope retention in single stars or substantial post-formation accretion. The upper boundary is similarly flexible, with values up to $161\,M_\odot$ possible. The dimensionless spin of the most massive black holes may approach unity, with implications for gravitational wave signatures and the formation of long-duration gamma-ray bursts.

Theoretical advances in nuclear reaction rate measurements, improved modeling of angular momentum transport, and more realistic treatments of binary interactions are needed to further constrain the mass gap boundaries. Observational data from gravitational wave detectors will continue to test these predictions and may reveal rare channels for the formation of exceptionally massive black holes.

Conclusion

This study provides a rigorous analysis of the physical processes that define the pair-instability mass gap for black holes, highlighting the sensitivity of the gap boundaries to nuclear reaction rates, binary evolution, rotation, and accretion. The findings suggest that the mass gap is a dynamic feature, shaped by both stellar physics and binary interactions, and that future developments in both theory and observation will be essential for a complete understanding of black hole formation in the universe.