Spherically Symmetric Scalar Hair for Charged Black Holes

Abstract: The no-hair theorem by Mayo and Bekenstein states that there exists no non-extremal static and spherical charged black hole endowed with hair in the form of a charged scalar field with a self-interaction potential. In our recent work, we showed that the effect of a scalar mass term is important at an asymptotic infinity, which was omitted to prove the no-hair theorem. In this paper, we demonstrate that there actually exists static and spherical charged scalar hair, dubbed as Q-hair, around charged black holes, by taking into account the backreaction to the metric and gauge field. We also discuss that Q-cloud, which is constructed without the backreaction around a Reissner-Nordström black hole, is a good approximation to Q-hair under a certain limit.

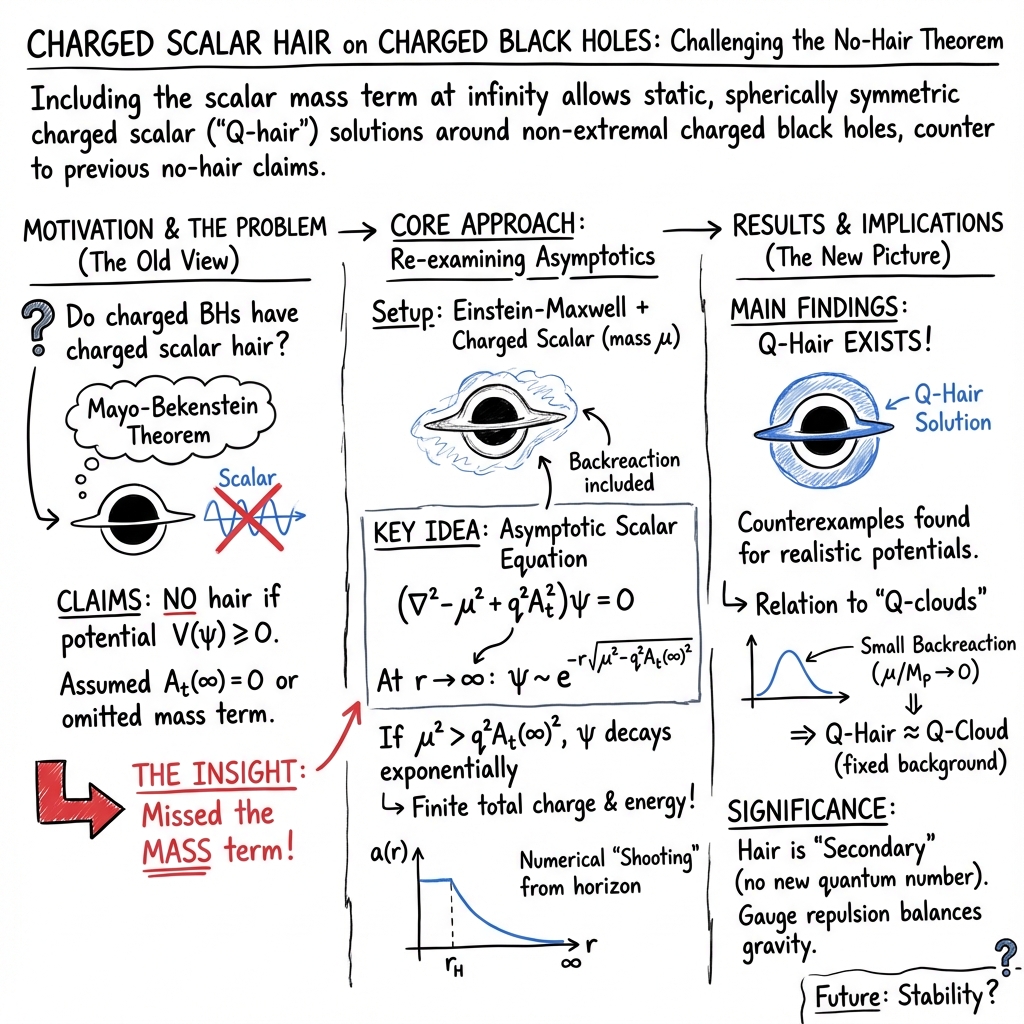
• The paper establishes that Q-hair can exist for charged black holes by incorporating scalar mass at asymptotic infinity.
• It employs numerical methods with a polynomial self-interaction potential to map the parameter space for viable scalar hair formations.
• The findings challenge conventional no-hair theorems, offering new perspectives on black hole properties and the interplay between gravity and quantum mechanics.

Detailed Summary of "Spherically Symmetric Scalar Hair for Charged Black Holes"

Introduction

The paper "Spherically Symmetric Scalar Hair for Charged Black Holes" (2004.03148) challenges longstanding assumptions derived from the no-hair theorem, particularly as articulated by Mayo and Bekenstein. The authors construct and analyze black hole solutions that possess scalar hair, which are specifically spherically symmetric and charged. They introduce the concept of Q-hair, showing that it exists even when the backreaction to the metric and gauge field is considered.

Context and Motivation

The work explores the ongoing discourse surrounding the no-hair theorem, which traditionally posits that black holes cannot support scalar hair. This notion has been reconciled with various fields in theoretical physics but remains contested in scenarios involving charged scalar fields. The foundational claim of Mayo and Bekenstein, which purports that non-extremal static spherical charged black holes lack scalar hair, is scrutinized through the lens of scalar mass considerations at asymptotic infinity, a factor previously overlooked. By re-examining these scenarios, the authors assert the existence of static, spherical charged scalar hair, or Q-hair, thereby contributing to the broader understanding of gravity and quantum mechanics at the interface of black hole physics.

Theoretical Framework and Equations of Motion

Central to the study is the action comprising a U(1) gauge field coupled with a charged scalar field interacting with gravity. The authors employ a theoretical model that incorporates the effects of scalar mass and its contribution to the dynamics of the system, even at large distances from the black hole. The paper presents detailed equations governing the system, highlighting how modifications to traditional assumptions about asymptotic behavior, particularly concerning scalar mass, can yield solutions that permit the existence of scalar hair.

Numerical Solutions and Results

The authors demonstrate numerical solutions revealing the presence of Q-hair around charged black holes. These solutions are generated using a polynomial self-interaction potential for the scalar field. The results show that Q-hair can indeed form under certain conditions, and the paper provides a parameter space mapping where such configurations are viable.

Figure 1: Solutions of $\psi(r)$ (solid lines) and $q\tilde{A}_t(r)$ (dashed lines) for varying $\mu$.

Essentially, the paper establishes that under non-negligible scalar masses, the no-hair theorem does not hold, and consistent solutions exist where the scalar field and gauge field display monotonic behavior from the black hole horizon to asymptotic regions.

Figure 2: Plot illustrating the parameter space for the existence of Q-hair.

Implications and Future Directions

The findings significantly impact theoretical physics by providing counterexamples that challenge existing no-hair conjectures. Q-hair solutions impact how charged black holes might interact with surrounding matter fields, providing new insights into black hole properties and their interaction with scalar fields. In practical terms, this research opens up new avenues for exploring black holes' interactions with various field configurations and has implications for understanding the quantum mechanical aspects of gravitational systems.

Further investigations could explore the dynamic stability and robustness of these hair solutions against perturbations, an area the authors suggest as a direction for future research. The potential for Q-hair solutions in more complex environments, such as rotating black holes or those interacting with other fields, could expand the understanding of black hole physics beyond the current theoretical models.

Conclusion

Overall, the paper presents a significant step forward in black hole research, notably in scenarios involving charged fields where conventional no-hair assertions are challenged. By incorporating previously neglected aspects like scalar mass at infinity, the authors provide robust evidence of scalar hair formation, thus offering new insights into the enigmatic nature of black holes. This study reinforces the complexity of these astronomical entities and underscores the intricate blending of general relativity and quantum mechanics in theoretical physics.