Anomalous dispersion relations in the staggered flux state (1711.04982v1)

Abstract: We study the quasiparticle properties in the d-wave superconductivity, antiferromagnetism, and the staggered flux state within a renormalized mean-field theory based on the two-dimensional t-J model. In particular, we focus on the anomalous quasiparticle dispersion relations around the antinodal region of the Brillouin zone argued in Hashimoto et al., Nature Phys. 6, 414 (2010). We obtain the qualitatively consistent results with their observations when we take account of the SF state. The present analysis shows that the SF order can be a possible candidate of symmetry-breaking pseudogap states coexisting with the dSC.

• The paper demonstrates that the staggered flux state produces anomalous quasiparticle dispersion relations in the antinodal region, supporting its candidacy for pseudogap states.
• It employs an advanced renormalized mean-field theory and BdG equations on a 2x2 lattice to characterize differences between d-wave superconductivity and SF states.
• Results indicate a higher excitation gap in the SF state compared to dSC, emphasizing minimal influence from antiferromagnetic order on dispersion.

Anomalous Dispersion Relations in the Staggered Flux State

Introduction

The paper "Anomalous dispersion relations in the staggered flux state" explores the quasiparticle properties associated with d-wave superconductivity (dSC), antiferromagnetism (AF), and the staggered flux (SF) state using a renormalized mean-field theory based on the two-dimensional $t$-$J$ model. This investigation primarily targets the anomalous quasiparticle dispersion relations discerned in the antinodal region of the Brillouin zone. The research reveals that the SF order is a viable candidate for the symmetry-breaking pseudogap states coexisting with dSC, corroborating findings by Hashimoto et al. regarding gap structures observed in Bi-2201.

Model and Methodology

The paper employs an advanced renormalized mean-field theory for the $t$-$J$ model with the Hamiltonian formulated as:

${\mathcal H} = -\sum_{\langle i,j \rangle,\sigma} P_{G}( t_{ij}c^{\dag}_{i\sigma} c_{j\sigma} + {\rm h.c.} )P_{G} + J\sum_{\langle i,j\rangle}\mbox{\boldmath $S_{i}\cdot S_{j}$} - \mu\sum_{i,\sigma}c^{\dag}_{i\sigma} c_{i\sigma}$

where $P_{G}$ is Gutzwiller's projection operator. The renormalized parameters are derived from cluster calculations to replicate variational Monte Carlo results. The methodology incorporates the Bogoliubov-de Gennes (BdG) equations within an extended Gutzwiller approximation framework. A 2x2 square lattice is regarded as a unit cell to accomplish numerical solutions of the BdG equations.

Results and Discussion

The quasiparticle states of dSC and SF are analyzed by computing the DOS and quasiparticle dispersion relations.

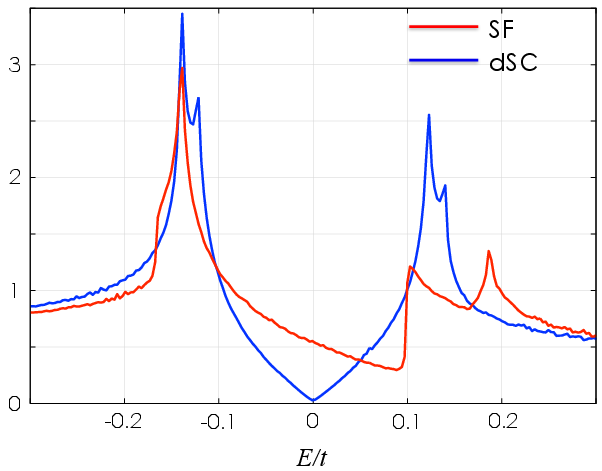
Figure 1: The density of states (DOS) per each site for dSC (blue) and SF (red) states.

The DOS for dSC and SF exhibit significant differences. In the antinodal region, the SF state's DOS is markedly shifted downwards compared to the dSC state, indicating a higher quasiparticle excitation energy in the SF state.

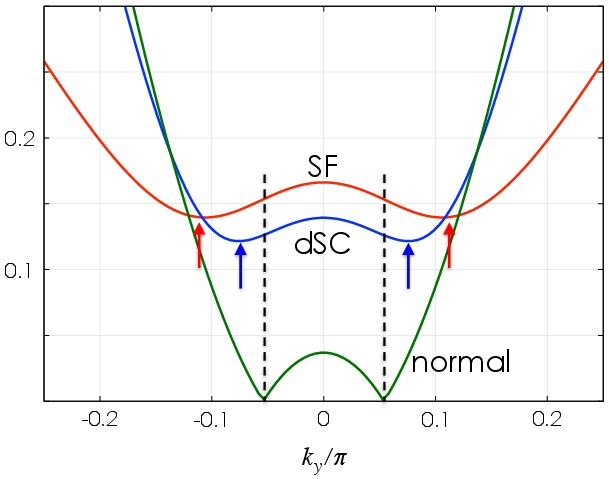
Figure 2: Quasiparticle dispersion relation for dSC (blue), SF (red), and the normal state (green) along the Brillouin zone boundary $k_x = \pi$.

The dispersion relation reveals that dSC has a superconducting energy gap while SF exhibits a larger excitation energy gap. This is consistent with recent ARPES observations which suggest SF could be a candidate for pseudogap states coexisting with dSC. The SF state's anomalous dispersion aligns with the broken particle-hole symmetry observed experimentally.

Influence of Antiferromagnetic Order

The paper examines the potential effects of AF order on the quasiparticle dispersion. Although a small degree of coexisting AF order is found, its influence on the dispersion relation is relatively negligible compared to the SF state.

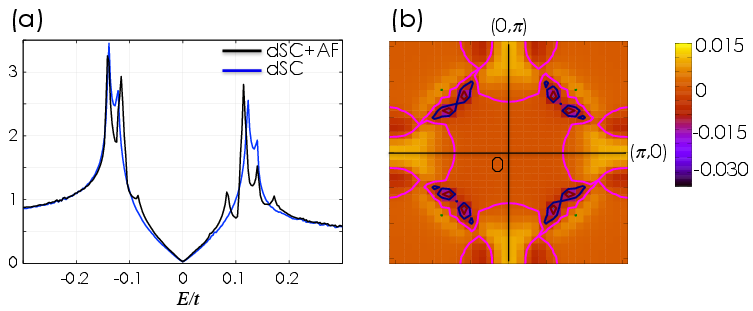
Figure 3: (a) The DOS for the dSC state coexisting with AF order. (b) The difference of the momentum distribution functions between the dSC and the coexisting state.

The differences in DOS and momentum distribution highlight a minor impact from AF order, thereby indicating that SF state anomaly does not directly arise from AF effects.

Conclusion

The paper significantly contributes to understanding quasiparticle dispersion relations in high-Tc cuprate superconductors. The SF state emerges as a pertinent candidate for pseudogap states, potentially altering future research approaches to symmetry-breaking phenomena. Antiferromagnetic order does not substantially affect dSC, implying SF's anomalous characteristics could pave the way for further investigations into pseudogap dynamics in cuprate materials. The findings spur more profound exploration into SF state's coexistence with dSC beyond current theoretical confines.

Future developments may explore finite temperature effects and intersite Coulomb repulsions to provide deeper insights into the stabilization of SF states coexisting with dSC.