Analysis of classifiers' robustness to adversarial perturbations (1502.02590v4)

Abstract: The goal of this paper is to analyze an intriguing phenomenon recently discovered in deep networks, namely their instability to adversarial perturbations (Szegedy et. al., 2014). We provide a theoretical framework for analyzing the robustness of classifiers to adversarial perturbations, and show fundamental upper bounds on the robustness of classifiers. Specifically, we establish a general upper bound on the robustness of classifiers to adversarial perturbations, and then illustrate the obtained upper bound on the families of linear and quadratic classifiers. In both cases, our upper bound depends on a distinguishability measure that captures the notion of difficulty of the classification task. Our results for both classes imply that in tasks involving small distinguishability, no classifier in the considered set will be robust to adversarial perturbations, even if a good accuracy is achieved. Our theoretical framework moreover suggests that the phenomenon of adversarial instability is due to the low flexibility of classifiers, compared to the difficulty of the classification task (captured by the distinguishability). Moreover, we show the existence of a clear distinction between the robustness of a classifier to random noise and its robustness to adversarial perturbations. Specifically, the former is shown to be larger than the latter by a factor that is proportional to \sqrt{d} (with d being the signal dimension) for linear classifiers. This result gives a theoretical explanation for the discrepancy between the two robustness properties in high dimensional problems, which was empirically observed in the context of neural networks. To the best of our knowledge, our results provide the first theoretical work that addresses the phenomenon of adversarial instability recently observed for deep networks. Our analysis is complemented by experimental results on controlled and real-world data.

• The paper establishes a theoretical upper bound on classifier robustness using a distinguishability measure, clarifying the gap between adversarial and random noise robustness.
• It demonstrates that linear classifiers struggle with closely spaced class means while quadratic classifiers leverage second-order moments for improved robustness.
• Empirical evaluations on MNIST and CIFAR-10 confirm that achieving high accuracy does not ensure resistance to adversarial attacks, highlighting a need for enhanced architectures.

Analysis of Classifiers' Robustness to Adversarial Perturbations

Introduction to Adversarial Instability

Adversarial perturbations reveal a critical vulnerability in classifiers, particularly deep networks, by inducing minimal changes to input data that lead to incorrect classifications. This paper establishes a theoretical framework to explore the classifiers' instability regarding such perturbations, proposing upper bounds on robustness and exploring the implications for linear and quadratic classifiers. By analyzing classifiers in tasks with low distinguishability, the paper emphasizes the inherent limitations in achieving robustness alongside accuracy.

Theoretical Framework for Robustness

The primary contribution is a general upper bound on classifiers' robustness to adversarial perturbations, predicated on a distinguishability measure reflecting classification task difficulty. For linear classifiers, distinguishability is related to the distance between class means. Quadratic classifiers, conversely, consider second-order moments. This distinction underscores the discrepancy between robustness to adversarial vs. random noise, explaining empirical observations from preceding research.

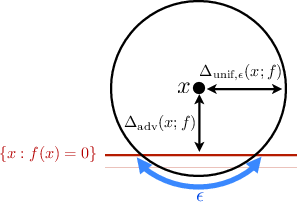
Figure 1: Illustration of the distinguishability measure impacting robustness in classifiers.

Adversarial Perturbations vs. Random Noise

The paper distinguishes between robustness to adversarial and random uniform noise, asserting that for linear classifiers, robustness to random noise exceeds that to adversarial perturbations by a factor proportional to the square root of the signal dimension, $d$. This theoretically supports empirical findings showing classifiers' differential vulnerability to noise types, especially in high-dimensional settings.

Figure 2: Depiction of robustness comparison between random noise and adversarial perturbations.

Practical Analysis through Case Studies

Linear Classifiers

Applying the theoretical bounds to linear classifiers reveals a fundamental limitation in tasks with close class means—a criterion for distinguishability. In such cases, achieving high accuracy does not guarantee robustness, as minuscule perturbations can alter classifier output. The graphical depiction shows non-achievable zones by linear classifiers, illuminating robustness gaps.

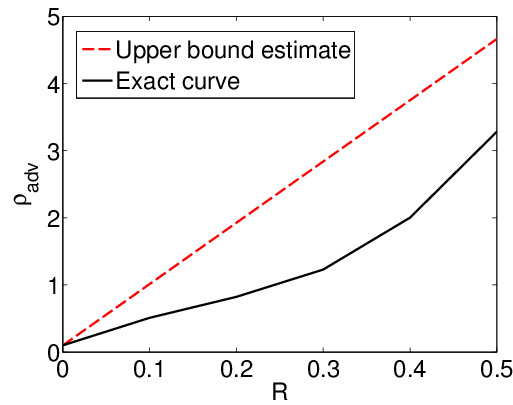
Figure 3: Graphical representation of non-achievable robustness zones for linear classifiers.

Quadratic Classifiers

Quadratic classifiers inherently possess a more flexible structure, allowing for greater robustness due to their consideration of second-order statistical moments. This flexibility results in higher adversarial robustness in scenarios where linear classifiers falter, as demonstrated by the theoretical bounds and empirical analysis.

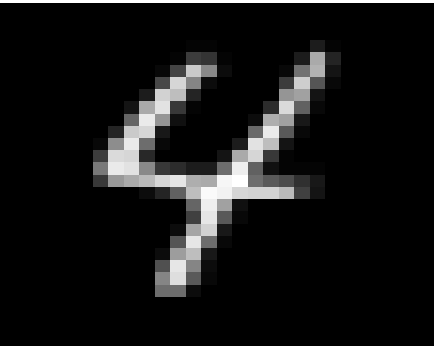
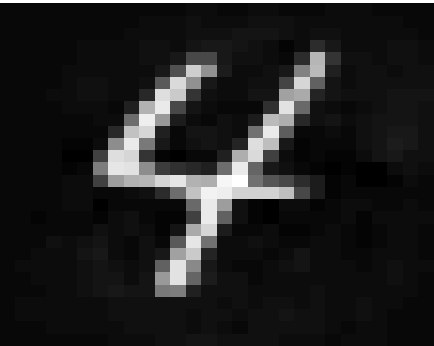
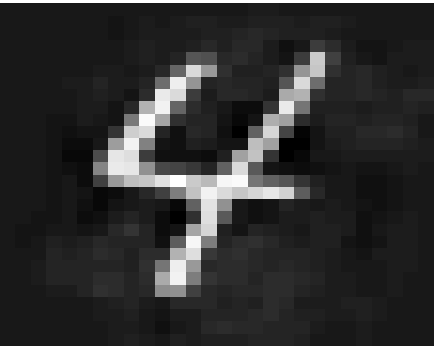
Figure 4: Enhanced robustness visualization for quadratic classifiers in tasks with distinct second-order moments.

Experimental Verification

The theoretical insights were corroborated through experiments on real-world datasets, including the MNIST digits and CIFAR-10 natural images. These datasets serve as vehicles for demonstrating classifiers' robustness limits, further validated by empirical risk assessments and robustness estimations. The experiments reiterate the paper's fundamental assertion—classification systems can achieve high accuracy without being robust to adversarial conditions, warranting improved methodologies and more flexible architectures for adversarial resistance.

Figure 5: Experimental results showing classifiers' performance and adversarial vulnerabilities across datasets.

Conclusion and Future Directions

This paper provides the initial theoretical analysis linking classifiers' complexity with adversarial robustness, advocating for advancements in design and training methods to overcome identified limitations. Future research should explore diverse classifier families, including deep networks, under this framework to enhance robustness. Moreover, real-world applicability and better understanding of domain-specific perturbations remain critical frontiers.

Through rigorous examination and concrete case studies, this work offers a foundational perspective for advancing AI systems' resilience to adversarial perturbations.