Asymmetric numeral systems

Abstract: In this paper will be presented new approach to entropy coding: family of generalizations of standard numeral systems which are optimal for encoding sequence of equiprobable symbols, into asymmetric numeral systems - optimal for freely chosen probability distributions of symbols. It has some similarities to Range Coding but instead of encoding symbol in choosing a range, we spread these ranges uniformly over the whole interval. This leads to simpler encoder - instead of using two states to define range, we need only one. This approach is very universal - we can obtain from extremely precise encoding (ABS) to extremely fast with possibility to additionally encrypt the data (ANS). This encryption uses the key to initialize random number generator, which is used to calculate the coding tables. Such preinitialized encryption has additional advantage: is resistant to brute force attack - to check a key we have to make whole initialization. There will be also presented application for new approach to error correction: after an error in each step we have chosen probability to observe that something was wrong. There will be also presented application for new approach to error correction: after an error in each step we have chosen probability to observe that something was wrong. We can get near Shannon's limit for any noise level this way with expected linear time of correction.

• The paper introduces ANS as an innovative entropy coding technique that efficiently integrates compression with encryption using tailored probability distributions.
• It details a stream coder mechanism that maintains an internal state within a defined interval to optimize symbol encoding based on symbol probabilities.
• The study demonstrates ANS’s potential in error correction near Shannon's limit by dynamically reallocating redundancy across interconnected blocks.

Asymmetric Numeral Systems

Asymmetric Numeral Systems (ANS) is a family of entropy coding schemes that extends traditional numeral systems to encode symbols based on freely chosen probability distributions. This approach offers advantages over traditional methods like arithmetic coding by requiring only one state instead of two and allowing for simpler and faster implementations. ANS encompasses both the Asymmetric Binary System (ABS) for binary cases and the general Asymmetric Numeral Systems for larger symbol sets. Additionally, ANS can incorporate encryption by utilizing a pseudorandom number generator (PRNG) for encoding table initialization, making it resilient to brute force attacks.

Stream Coding and Decoding

Stream coding and decoding in ANS involves designing a coder that can convert symbol sequences into bitstreams, optimizing based on symbol probabilities. The coder maintains an internal state within a defined interval, transferring bits when the state reaches the interval boundary.

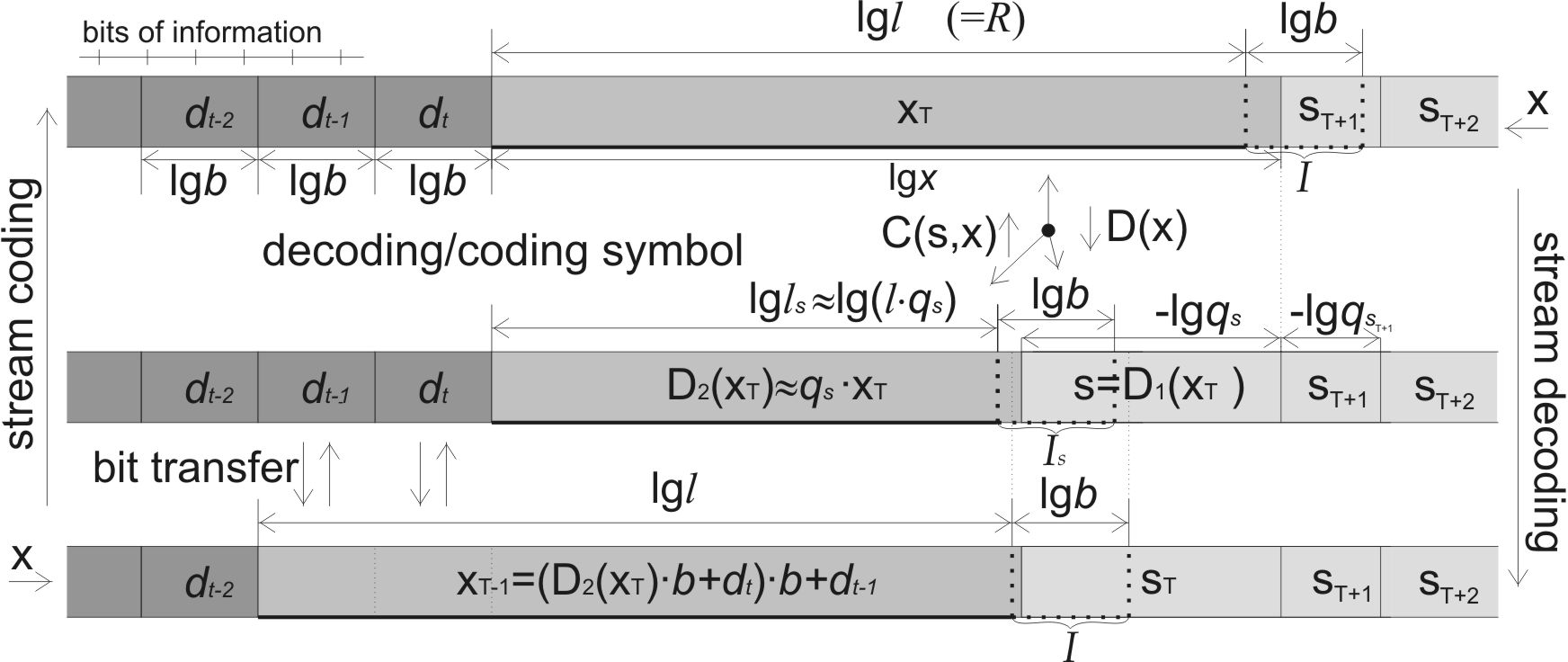
Figure 1: Stream coding/decoding.

The coder is initialized with a base ($b$) for numeral representation and an interval ($I$), ensuring that the internal state remains within the interval throughout processing. This is accomplished by transferring bits to/from the output when necessary, allowing ANS to efficiently handle data streams.

Asymmetric Numeral Systems

ANS generalizes the binary system to handle multiple symbols. It uses precomputed pseudorandom distributions tailored to symbol probabilities, which are initialized using PRNGs. This offers high precision and encryption capability, but may require re-initialization when symbol probabilities change.

The encoding precision is influenced by the size of tables and initialization methods. While precise coder initialization guarantees minimal redundancy, a self-correcting diffusion (ScD) mechanism offers quicker but less precise initialization. ANS's inherent flexibility allows encoding tables to be tailored to specific applications, providing tunable trade-offs between speed, precision, and memory usage.

Probabilistic Analysis and Correction Limits

Figure 2: Correction algorithm. It will create such (pseudo) random trees.

Probability distribution among coder states during processing tends to be inversely proportional to the state magnitude. This characteristic is leveraged in both encryption and error correction strategies. For encryption, this non-uniformity provides unpredictability. For error correction, ANS extends classic block codes by connecting redundancy among blocks, enabling error correction even with high local error concentrations. Through massively interconnected blocks, redundancy is dynamically reallocated to handle concentrations of errors, enabling corrections close to Shannon's limit.

Cryptographic Applications

ANS can be employed as a cryptographic tool by leveraging its initialization randomness and dynamic state management. Coding tables initialized with PRNG using a key offer throughput advantages over traditional encryptions which require real-time computation. Thus, ANS provides highly secure and efficient data encryption, resistant to adaptive attacks and brute force key discovery.

Considerations for Implementation

While ANS promises integration into advanced data compression and encryption systems, practical implementations must balance several parameters:

• State Management: Memory requirements and computational overhead need optimization by carefully choosing the state interval size and base $b$.
• Initialization Interfaces: Using existing PRNGs ensures integration into cryptographic protocols, allowing ANS to double as both an encoder and secure block cipher mechanism.
• Decoding Complexity: Designing a decoding path ensures redundancy checks and facilitates error correction, with fallback mechanisms for pathological cases.

Conclusion

Asymmetric Numeral Systems provide a versatile and powerful framework for both data compression and encryption. By offering adjustable precision and speed, ANS balance traditional codec efficiency with cryptographic security. ANS adoption not only pushes the boundaries of coding technology towards Shannon's limit but also enhances data reliability and authenticity in secure communications. As future developments improve ANS implementation strategies, this coding family is poised to impact a broad spectrum of data-driven applications.