VJEPA: Variational Joint Embedding Predictive Architectures as Probabilistic World Models

Abstract: Joint Embedding Predictive Architectures (JEPA) offer a scalable paradigm for self-supervised learning by predicting latent representations rather than reconstructing high-entropy observations. However, existing formulations rely on \textit{deterministic} regression objectives, which mask probabilistic semantics and limit its applicability in stochastic control. In this work, we introduce \emph{Variational JEPA (VJEPA)}, a \textit{probabilistic} generalization that learns a predictive distribution over future latent states via a variational objective. We show that VJEPA unifies representation learning with Predictive State Representations (PSRs) and Bayesian filtering, establishing that sequential modeling does not require autoregressive observation likelihoods. Theoretically, we prove that VJEPA representations can serve as sufficient information states for optimal control without pixel reconstruction, while providing formal guarantees for collapse avoidance. We further propose \emph{Bayesian JEPA (BJEPA)}, an extension that factorizes the predictive belief into a learned dynamics expert and a modular prior expert, enabling zero-shot task transfer and constraint (e.g. goal, physics) satisfaction via a Product of Experts. Empirically, through a noisy environment experiment, we demonstrate that VJEPA and BJEPA successfully filter out high-variance nuisance distractors that cause representation collapse in generative baselines. By enabling principled uncertainty estimation (e.g. constructing credible intervals via sampling) while remaining likelihood-free regarding observations, VJEPA provides a foundational framework for scalable, robust, uncertainty-aware planning in high-dimensional, noisy environments.

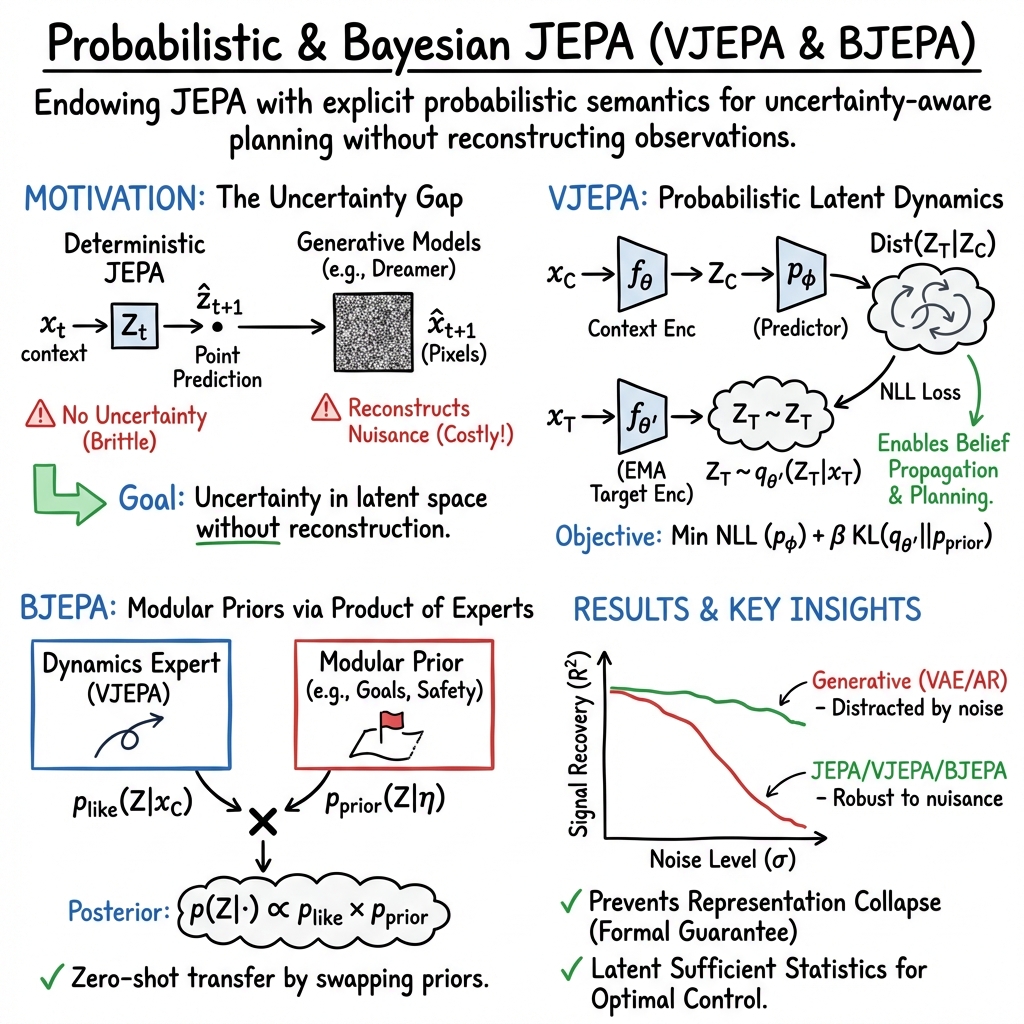
• The paper introduces VJEPA, extending JEPA with a variational objective for probabilistic latent state prediction in stochastic environments.
• It leverages Bayesian filtering and predictive state representations to enable uncertainty-aware planning and maintain signal recovery despite nuisance variability.
• Empirical results show that both VJEPA and its Bayesian variant, BJEPA, outperform generative models in filtering noise and robust control tasks.

Variational Joint Embedding Predictive Architectures as Probabilistic World Models

Introduction

The paper "VJEPA: Variational Joint Embedding Predictive Architectures as Probabilistic World Models" introduces Variational Joint Embedding Predictive Architecture (VJEPA), a probabilistic framework extending the Joint Embedding Predictive Architecture (JEPA). While traditional JEPA predicts latent representations, it typically relies on deterministic objectives, limiting its applicability in stochastic environments. VJEPA incorporates a variational objective to model the distribution of future latent states, integrating elements from Predictive State Representations (PSRs) and Bayesian filtering to enhance control tasks without reconstructing high-entropy observations.

Background and Motivation

Existing approaches in self-supervised representation learning, like generative modeling and contrastive learning, are limited in handling nuisance variability and require complex sampling schemes. JEPA offers a scalable alternative by predicting latent representations of data, emphasizing task-relevant structures and discarding unnecessary details. Recent works explore JEPA as a foundation for world models and planning but have not formalized the probabilistic semantics that underlie JEPA predictions.

VJEPA Framework

VJEPA extends JEPA by developing a predictive distribution over future latent states, addressing the absence of probabilistic semantics in current JEPA implementations. The paper leverages a variational approach to link VJEPA with PSRs and Bayesian filtering, formalizing its ability to serve as information states for optimal control. This allows VJEPA to provide uncertainty-aware planning and avoid the pitfalls of observation reconstruction.

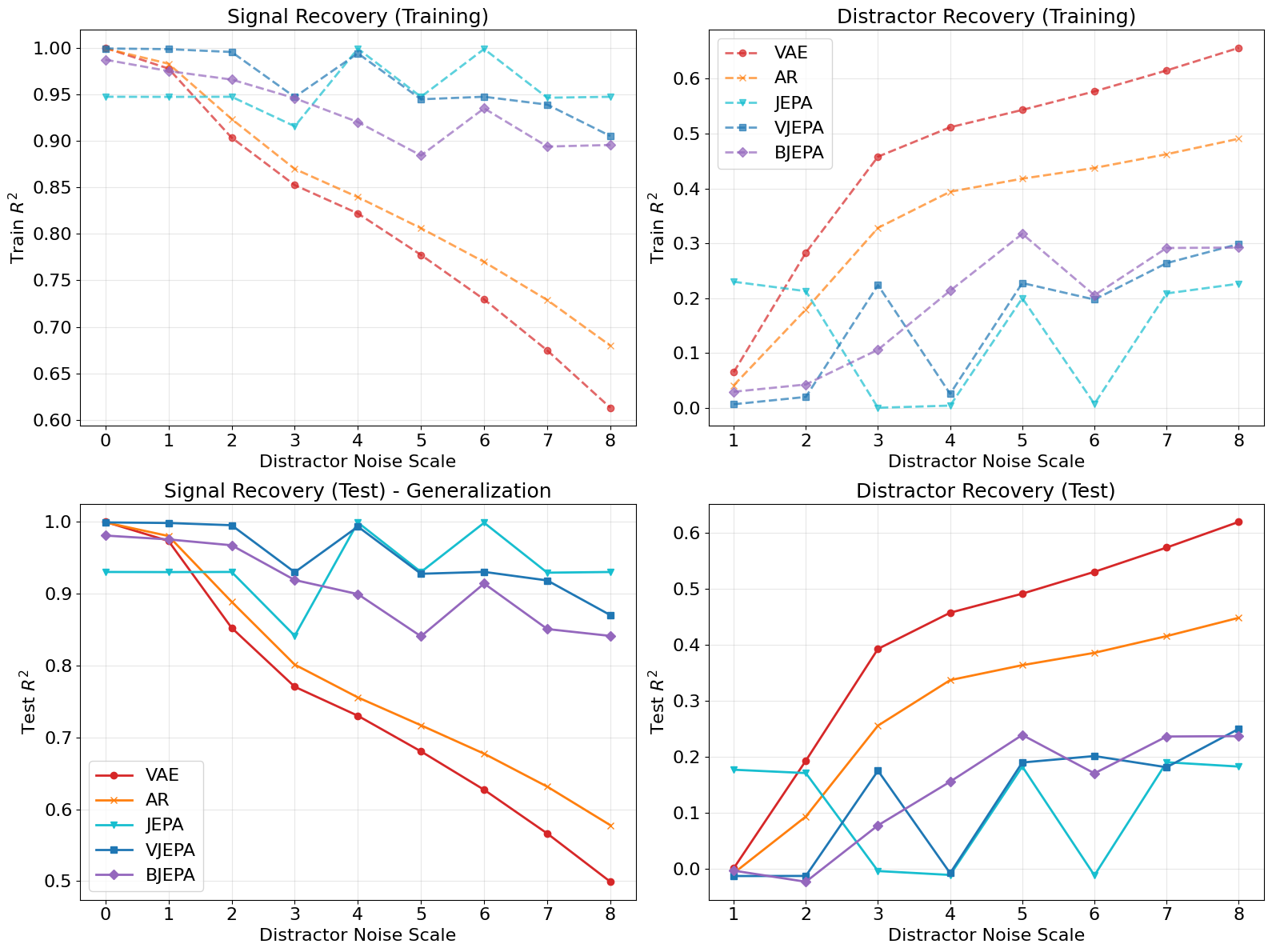
Figure 1: Performance metrics across noise scales. Top Row: Training set $R^2$. Bottom Row: Test set $R^2$ (Generalization). The generative models (VAE, AR) degrade linearly as noise increases, tracking the distractor (Bottom Right). The JEPA-based models (Blue/Cyan/Purple) maintain high signal recovery (Bottom Left) even at high noise scales, demonstrating invariance to nuisance variability.

Bayesian Extension: BJEPA

The paper introduces Bayesian JEPA (BJEPA), which extends VJEPA by factorizing the predictive belief into a learned dynamics expert and a modular prior expert. This allows the integration of structural priors for constraint satisfaction and zero-shot task transfer. BJEPA employs a Product of Experts approach to intersect future latent states with dynamically feasible and task-compliant constraints, enabling robust, modular, and task-adaptive world modeling.

Figure 2: Latent Reconstructions at varying noise scales. At $\sigma=8.0$ (Right), the VAE and AR reconstructions (dashed lines) track the high-frequency noise. In contrast, BJEPA and VJEPA (solid lines) successfully filter the noise and track the underlying true signal (black line).

Empirical Validation

Empirically, the paper demonstrates that both VJEPA and BJEPA effectively handle high-variance distractors in a noisy environment experiment, where generative models failed. VJEPA and BJEPA maintain high signal recovery, showcasing robustness and invariant performance to nuisance variability. This empirically supports the theoretical assertion that VJEPA can achieve principled uncertainty estimation without reliance on autoregressive observation likelihoods.

Implications and Future Directions

The introduction of VJEPA and BJEPA suggests new pathways for scalable, robust, uncertainty-aware planning in high-dimensional environments. These models could significantly impact applications in robotics and autonomous systems, where observation reconstruction is often impractical. Future research may explore more expressive architectures for predictive distributions and further refine the integration of structural priors to optimize task-specific world modeling.

Conclusion

The development of VJEPA represents a critical step forward in bridging deterministic predictive learning with probabilistic modeling. By formalizing the probabilistic underpinnings and extending JEPA into a variational framework, VJEPA and its Bayesian variant, BJEPA, provide a rich foundation for developing robust, uncertainty-aware models capable of handling stochastic environments without explicit reconstruction tasks. This work aligns with the overarching goal of advancing autonomous decision-making in complex, high-dimensional spaces.