Embedded Universal Predictive Intelligence: a coherent framework for multi-agent learning (2511.22226v1)

Abstract: The standard theory of model-free reinforcement learning assumes that the environment dynamics are stationary and that agents are decoupled from their environment, such that policies are treated as being separate from the world they inhabit. This leads to theoretical challenges in the multi-agent setting where the non-stationarity induced by the learning of other agents demands prospective learning based on prediction models. To accurately model other agents, an agent must account for the fact that those other agents are, in turn, forming beliefs about it to predict its future behavior, motivating agents to model themselves as part of the environment. Here, building upon foundational work on universal artificial intelligence (AIXI), we introduce a mathematical framework for prospective learning and embedded agency centered on self-prediction, where Bayesian RL agents predict both future perceptual inputs and their own actions, and must therefore resolve epistemic uncertainty about themselves as part of the universe they inhabit. We show that in multi-agent settings, self-prediction enables agents to reason about others running similar algorithms, leading to new game-theoretic solution concepts and novel forms of cooperation unattainable by classical decoupled agents. Moreover, we extend the theory of AIXI, and study universally intelligent embedded agents which start from a Solomonoff prior. We show that these idealized agents can form consistent mutual predictions and achieve infinite-order theory of mind, potentially setting a gold standard for embedded multi-agent learning.

• The paper introduces a novel embedded Bayesian framework that integrates an agent’s policy with environment dynamics to overcome nonstationarity in multi-agent settings.
• It employs universal sequence prediction with reflective oracles to enable infinite-order theory of mind and joint action–percept forecasting.
• Empirical results indicate that embedded agents converge to cooperative equilibria in social dilemmas, outperforming traditional Nash-based methods.

Embedded Universal Predictive Intelligence: A Coherent Framework for Multi-Agent Learning

Introduction and Motivation

The paper "Embedded Universal Predictive Intelligence: a coherent framework for multi-agent learning" (2511.22226) addresses foundational limitations of current reinforcement learning (RL) paradigms in multi-agent settings. Classical RL assumes agents are decoupled from the environment, which is modeled as stationary. However, multi-agent systems are inherently non-stationary due to the simultaneous learning and adaptation of multiple agents, leading to mutual influence and infinite recursive reasoning (theory of mind).

The work introduces a formal framework that (1) embeds agents within their universes—considering their own policy as part of the environment—which allows agents to reason about themselves, and (2) leverages universal Bayesian sequence prediction for joint action–percept forecasting. This paradigm is motivated both by theoretical desiderata (overcoming failures of Nash equilibrium in social dilemmas) and the practical trajectory of foundation model-based learning architectures.

Figure 1: Embedded Bayesian agents model themselves as part of the universe, maintaining beliefs over both environment and self-policy, enabling structural similarity reasoning and equilibrium selection unattainable by decoupled agents.

Embedded Bayesian Agents: From Decoupled to Embedded Agency

Standard Bayesian RL operates with a prior and posterior over environments, updating beliefs upon new percepts. This suffices in single-agent and some tractable multi-agent scenarios but fails conceptually and practically in general multi-agent structures, especially when recursive modeling (theory of mind) affects the agents' future.

Embedded Bayesian agents instead maintain beliefs over universes (joint programs combining environment dynamics and agent policies, including their own), and crucially update their beliefs both upon new percepts and upon their own actions—enabling them to predict both future inputs and their own decision process. This is formalized by a universal Bayesian mixture over a countable class of universe semimeasures.

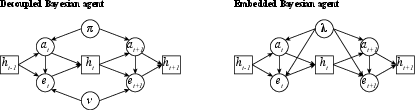
Figure 2: Graphical models illustrating the distinction between decoupled (left) and embedded (right) Bayesian agents; embedded models joint action–percept histories, coupling updates about self and environment.

This embedded perspective leads to two technical axes:

1. Prospective Learning: Embedded agents performing joint action–percept sequence prediction can anticipate both their own learning and that of others, generalizing the notion of co-player learning aware RL to a fully Bayesian, nonparametric model class.
2. Structural Similarity and Coupled Beliefs: By reasoning over universes, actions taken by the agent inform its beliefs over the environment (including other agents), allowing strong forms of theory of mind and similarity-aware inference.

These concepts are not ad hoc; the work proves that under universal algorithmic priors (Solomonoff), universes with similar agents are favored by Occam’s razor due to shorter description lengths, establishing that mutual information between agent and environment is generically positive.

Embedded Universal Predictive Intelligence and the Grain-of-Truth Problem

The grain-of-truth problem is the challenge of defining agent model classes such that the class contains the true model including the learning agent itself. In standard AIXI (universal RL), the agent is not contained in its own model class due to self-reference limits; this failure is acute in multi-agent and recursive settings.

The paper resolves this via:

• Reflective Oracles: Environments are described as oracle Turing machines with access to a reflective oracle, which allows the construction of fixed points where the agent’s own policy (even if itself Bayesian or universal) is within the model class. This resolves infinite regress in mutual prediction.
• Reflective Universal Inductor (RUI): Alternatively, a universal Bayesian prior is placed over reflexive universe-generating machines (programs that can themselves invoke the universal inductor), allowing for consistent predictions and infinite-order theory of mind.

  Figure 3: Comparison between Decoupled Agency (AIXI, left) where agent and environment are separate, and Embedded Agency (MUPI framework, right) where agent and environment are unified within a joint universe capable of reflective inference.

Joint prediction of self-action and external percepts induces a new class of solution concepts in game-theoretic analysis:

• Embedded Equilibria (EE): Allow rational agents to select behaviors reflecting structural similarities and evidential influence, often supporting cooperation unattainable in Nash equilibria under classical decision theory.
• Subjective Embedded Equilibria (SEE): Characterize the convergence of embedded Bayesian agents with mutual prediction aware policies and beliefs.

Strong Claims and Numerical Results

Strong claims/results from the paper:

• Convergence Guarantees: Agents employing embedded Bayesian logic with a suitably broad hypothesis class (with grain-of-truth) are guaranteed to converge to $\epsilon$-subjective embedded equilibria in general multi-agent settings, under minimal assumptions.
• Infinite Theory of Mind: Embedded agents with universal inductive structure (MUPI) obtain infinite-order theory of mind, forming consistent mutual predictions even as policies recursively depend upon each other.
• Provable Superiority: In mixed-motive social dilemmas (e.g., twin Prisoner’s Dilemma), embedded Bayesian agents converge to cooperative (Pareto superior) equilibria, in sharp contrast to model-free or causally-decoupled agents that defect.

Novel extensions include:

• Algorithmic formalization that the Solomonoff prior always induces coupled beliefs—the mutual information between policy and environment is always positive.
• Practical methods for constructing both the agents and their hypothesis classes using either reflective oracles or RUIs, resolving inherent self-reference.

Game-theoretic Implications and Decision-theoretic Alignment

These advances reify the connection between evidential (EDT), as opposed to causal (CDT), decision theory within algorithmic agents. Embedded agents’ self-models enable them to treat their own actions as evidence about structurally similar agents, rationalizing cooperation in the face of social dilemmas and defusing coordination failures endemic to Nash equilibria assumptions.

The solution concepts introduced—subjective and objective embedded equilibria—extend the landscape of multi-agent learning:

• SEE/EE generalize and strictly subsume Nash: Any Nash equilibrium is an EE (with decoupled beliefs), but EEs permit correlated deviations contingent upon evidential reasoning routes (e.g., self-referential policy updates).
• Subjective–Objective gap: While Bayesian learning in decoupled frameworks converges (in the limit) to Nash or correlated equilibrium, embedded Bayes-optimal learning can stably support more cooperative or otherwise unattainable behaviors.

Theoretical and Practical Implications, Future Developments

Theoretical Implications

• Embedded mutual modeling is necessary for social intelligence in agents that must robustly navigate non-stationary and highly interdependent environments (emergent lawmaking, negotiation, coalition formation).
• Algorithmic priors matter: The structure of universes considered by the agent—particularly those induced by algorithmic information theory—prescribe the degree of social/coupled inference attainable.
• Robustness to recursive paradox: The constructions presented sidestep infinite loops in mutual modeling, demonstrating that reflective Bayesian agents can be made both computationally consistent and game-theoretically stable.

Practical and AI Systems Implications

• Alignment with current LLM paradigms: Joint action-percept prediction in MUPI closely matches the architecture of contemporary foundation models designed for in-context RL and agentic deployment.
• Multi-agent Foundation Models: The MUPI principles suggest that suitably trained (and inductively regularized) foundation models could realize emergent social intelligence, theory of mind, and robust cooperation among similar agents.
• Dealing with Nonstationarity: Embedded prospective learning offers a principled route to avoid the pitfalls of retrospective RL and overfitting to stale data.
• Safe and Efficient Social Scaling: By favoring agents with similar structure (e.g., via training or model replication), the system can promote self-coordination with minimal explicit communication, with potential applications from multi-robot teams to AI-based governance.

Limitations and Open Directions

• Computational Intractability: While conceptually universal, embedded Bayes-optimal agents are incomputable; however, the theory motivates practical relaxations using scalable approximations in neural sequence models, with attention to the grain-of-truth deficit.
• Exploration and Dogmatic Beliefs: As with all Bayesian learners, embedded agents can acquire dogmatic, suboptimal strategies if exploration is not sufficiently incentivized; future work is needed on robust exploration in embedded settings.
• Empirical Validation: While the theoretical results are strong, empirical work on large-scale foundation models acting as embedded agents is required to substantiate the claims about practical coordination, cooperation, and sociality in real deployments.
• Decentralized Mutual Modeling: Extending these principles to guarantee mutual prediction and infinite theory of mind when agents have locally learned/self-supervised models, not preset by a common oracle or fixed point computation, remains an open challenge.

Conclusion

The paper provides a rigorous, algorithmically well-grounded framework (MUPI) for embedding social reasoning, infinite-order theory of mind, and evidential decision making into multi-agent RL agents via joint Bayesian prediction and reflective inference. It significantly advances the theoretical underpinnings of AI sociality and sets a clear path toward the deployment of foundation models capable of robust, cooperative multi-agent behavior in open-ended, nonstationary environments. The open problems—especially relating to efficient approximation, safe exploration and alignment—will define both the frontiers of AI safety research and the eventual societal impact of artificial multi-agent systems.