The Interplay between Bayesian Inference and Conformal Prediction

Abstract: Conformal prediction has emerged as a cutting-edge methodology in statistics and machine learning, providing prediction intervals with finite-sample frequentist coverage guarantees. Yet, its interplay with Bayesian statistics, often criticised for lacking frequentist guarantees, remains underexplored. Recent work has suggested that conformal prediction can serve to "calibrate" Bayesian credible sets, thereby imparting frequentist validity and motivating deeper investigation into frequentist-Bayesian hybrids. We further argue that Bayesian procedures have the potential to enhance conformal prediction, not only in terms of more informative intervals, but also for achieving nearly optimal solutions under a decision-theoretic framework. Thus, the two paradigms can be jointly used for a principled balance between validity and efficiency. This work provides a basis for bridging this gap. After surveying existing ideas, we formalise the Bayesian conformal inference framework, covering challenging aspects such as statistical efficiency and computational complexity.

• The paper introduces novel Bayesian CP methods that integrate the posterior predictive distribution with conformal machinery to ensure finite-sample coverage.
• It details full versus split CP approaches, proving that closed-form intervals in conjugate models can significantly enhance computational efficiency.
• Empirical findings confirm that Bayesian CP methods maintain frequentist validity and achieve Bayes-risk optimality, even under prior-data conflicts.

The Interplay between Bayesian Inference and Conformal Prediction: A Technical Examination

Introduction and Motivation

This paper systematically addresses the intersection of Bayesian inference and conformal prediction (CP), two major approaches for uncertainty quantification in statistics and machine learning. While Bayesian methods excel at propagating uncertainty via prior-to-posterior updates and highest-posterior predictive density (HPPD) intervals, they are often criticized for failing to deliver finite-sample frequentist coverage. In contrast, conformal methods guarantee coverage under minimal assumptions (exchangeability), but tend toward conservatism and inefficiency, especially in high-dimensional or structured data settings. The authors aim to synthesize these paradigms, providing formal frameworks where Bayesian probabilistic structure enhances conformal methods without sacrificing finite-sample validity, and conversely, where CP calibrates Bayesian predictions to guarantee frequentist error control.

Formal Frameworks for Bayesian Conformal Prediction

The paper provides an in-depth formalization of both full and split conformal prediction, integrating Bayesian machinery via the posterior predictive distribution (PPD). This integration yields "Bayesian CP" methods, which use the PPD as the conformity (or non-conformity) score within the CP machinery. The approach is twofold:

• Full Bayesian CP: The predictive set for a new observation is constructed by augmenting the observed data with candidate outcomes, evaluating the PPD under this augmented set, and inverting the associated test statistic or p-value. The theoretical basis for this construct is the exchangeability of conformity scores via data augmentation.
• Split Bayesian CP: To improve computational scalability, the sample is split into training and calibration sets. The training set is used to fit the Bayesian model, and the calibration set for empirical quantile adjustment. The authors provide new conformity scores, such as Bayesian residuals and PPD-based distances, tailored to leverage rich probabilistic information encoded in the posterior predictive.

Notably, the paper develops analytic, closed-form CP intervals for certain conjugate models (Normal-Normal-Gamma and Beta-Binomial), showing that equivalent conformity measures (ECMs) can dramatically simplify computation without altering statistical properties.

Bayes-Risk Optimality and Efficiency

A critical contribution is the rigorous justification of Bayesian CP intervals from a decision-theoretic perspective. By leveraging sufficiency and completeness properties, the authors show that full CP with PPD-based conformity scores is Bayes-risk optimal among all procedures with the same (or higher) frequentist coverage. They generalize Faulkenberry's method and establish the equivalence of certain ECMs in Normal and Binomial models, showing that computationally efficient conformity scores can be used without sacrificing optimality or validity.

The paper emphasizes that for models with boundedly complete regular sufficient statistics, there exists a unique Bayesian CP region that jointly achieves frequentist validity and minimal Bayes risk, explicitly highlighting that no other procedure can be uniformly more efficient within the class considered.

Computational Aspects

A major practical challenge for full Bayesian CP is scalability, due to the requirement to recompute Bayesian posteriors for each candidate outcome. The authors propose and formalize two efficient computational strategies:

• Add-One-In Importance Sampling: Recycles posterior draws from the observed data fit to compute the augmented PPD via importance weights, avoiding repeated MCMC runs.
• Leave-One-Out (LOO) Approximations: Especially for deleted (ECM) conformal schemes, the LOO approach leads to Bayes-optimal regions, is computationally feasible via marginal likelihood ratios, and addresses scenarios where Add-One-In fails (e.g., non-smooth models).

For conjugate models (e.g., Normal and Binomial), closed-form solutions for Bayesian CP intervals are derived, further reducing the computational overhead.

Empirical Results

Empirical studies under the Beta-Binomial model (with the Jeffreys prior) confirm that Bayesian CP methods consistently achieve coverage at or above the nominal level, while Bayesian HPPD can undercover or overcover depending on the prior and data alignment.

Figure 1: Empirical coverage and relative interval width for Bayesian CP variants under the Binomial model and Jeffreys prior at nominal level 0.9 with 1000 Monte Carlo replications.

The analytic Bayesian CP interval matches the performance of full CP with substantial computational savings. Split variants are less efficient but more scalable, as expected. Strong prior-data conflict induces undercoverage in HPPD intervals but not in Bayesian CP, highlighting the robustness of conformalization.

Theoretical and Practical Implications

Frequentist-Bayesian Synthesis

The findings establish a rigorous pathway for balancing Bayesian efficiency and frequentist validity. The hybrid approach allows for Bayesian models—including hierarchical structures and rich priors—to inform predictive inference, while the conformal wrapper enforces error control compliant with regulatory and scientific standards.

Extensions and Open Problems

The authors identify several domains for further research:

• Conditional Coverage: Marginal validity is guaranteed, but conditional coverage remains elusive in a distribution-free setting. Density-driven conformity scores (e.g., PPD-based) show promise for improved local coverage and asymptotic conditional validity.
• Departures from Exchangeability: Real datasets often lack global exchangeability. Local or partial exchangeability, as formalized in hierarchical Bayesian models, enables valid CP intervals in complex, structured data (e.g., grouped or multilevel data) and is amenable to further theoretical development.
• Small Area Estimation: In applications such as small area estimation, Bayesian CP intervals reconcile precise hierarchical modeling with robust finite-sample coverage, addressing critical needs in official statistics and policy-making.

Bayesian Highest Posterior Predictive Density and Conformal Regions

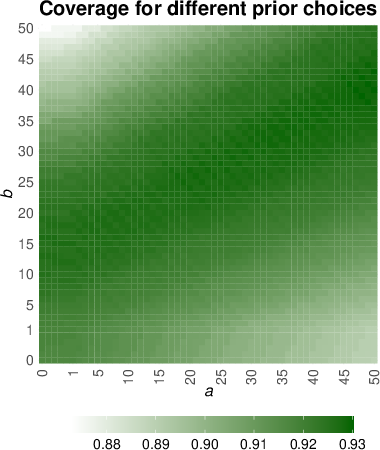
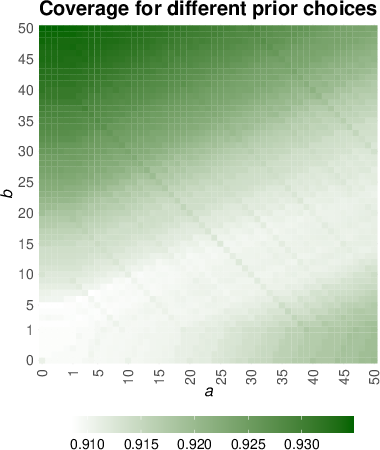
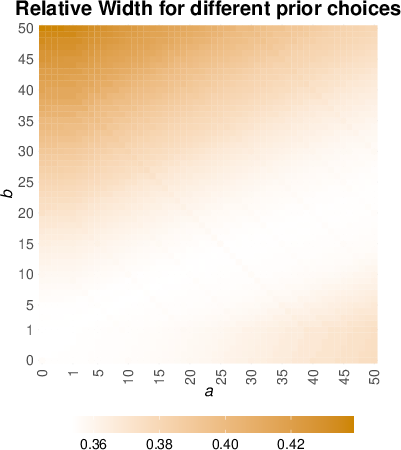
Figure 2: Bayesian HPPD interval visualization.

The visualization underscores the relationship between Bayesian HPPD intervals and conformal prediction sets, especially in the context of coverage behavior under model misspecification or prior misalignment.

Conclusion

This paper establishes a comprehensive and formal bridge between Bayesian inference and conformal prediction, providing theoretical optimality guarantees, efficient computational algorithms, and analytic results for key statistical models. The proposed frameworks empower practitioners to construct predictive regions that are both interpretable (in the Bayesian sense) and trustworthy (in the frequentist sense). The implications extend to uncertainty quantification for hierarchical and structured data and motivate future work on local validity and adaptive modeling within this hybrid paradigm.