Unbiased Primordial Gravitational Wave Inference from the CMB with SMICA (2510.26767v2)

Abstract: The detection of primordial gravitational waves in Cosmic Microwave Background B-mode polarization observations requires accurate and robust subtraction of astrophysical contamination. We show, using a blind Spectral Matching Independent Component Analysis, that it is possible to infer unbiased estimates of the primordial B-mode signal from ground-based observations of a small patch of sky even for highly complex foreground contamination. This work, originally performed in the context of configuration studies for a future CMB-S4 observatory, is highly relevant for the analysis of observations by the current generation of CMB experiments.

• The paper demonstrates that SMICA effectively recovers the primordial tensor-to-scalar ratio r using blind component separation even with complex foregrounds.
• It shows that adjusting the number of foreground components (n_FG) is critical to managing the bias-variance tradeoff in the presence of medium- to high-complexity foregrounds.
• The study validates the use of SVD-based diagnostics and realistic simulations to optimize CMB analysis strategies for current and future experiments.

Unbiased Inference of Primordial Gravitational Waves from the CMB with SMICA

Introduction and Motivation

The detection of primordial gravitational waves (PGWs) via the $B$-mode polarization of the Cosmic Microwave Background (CMB) is a central objective in observational cosmology, providing a direct probe of inflationary physics. The tensor-to-scalar ratio $r$ quantifies the amplitude of these primordial tensor perturbations relative to scalar perturbations. Achieving unbiased and precise measurements of $r$ is complicated by the presence of astrophysical foregrounds—primarily Galactic dust and synchrotron emission—which are orders of magnitude brighter than the expected PGW signal. The challenge is further exacerbated by the complexity and spatial variability of these foregrounds, as well as instrumental noise and lensing-induced $B$-modes.

This work systematically investigates the application of Spectral Matching Independent Component Analysis (SMICA), a blind component separation technique, to infer unbiased estimates of $r$ from simulated ground-based CMB observations, even in the presence of highly complex foregrounds. The paper is performed in the context of CMB-S4-like experimental configurations but is directly relevant to current and near-future CMB experiments.

Simulated Observations and Foreground Complexity

The analysis is based on detailed simulations of a low-foreground sky patch in the Southern Galactic hemisphere, adopting instrument parameters and noise models consistent with CMB-S4 specifications. The simulations incorporate multiple frequency channels, realistic beam profiles, and both white and $1/f$ noise components. Foreground emission is modeled using the PySM3 suite, with three levels of complexity:

• Low-complexity: Rigid frequency scaling for dust and synchrotron.
• Medium-complexity: Spatially varying frequency scaling.
• High-complexity: Additional anomalous microwave emission (AME), spectral running, and line-of-sight decorrelation.

The CMB signal is generated as a Gaussian random field, with delensing applied to reduce lensing $B$-mode contamination. The resulting mock observations combine CMB, foregrounds, and noise, providing a stringent testbed for component separation.

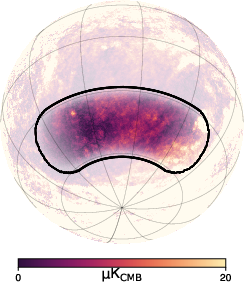
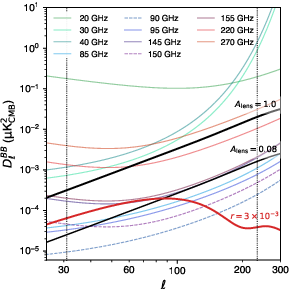
Figure 1: Sky patch (left) with binary outline traced in black, centered at (RA~=~$10^\circ$, dec~=~$-45^\circ$). The apodization yields $f_\text{sky}=2.5\%$. The right panel shows beam-deconvolved noise curves for both experimental configurations, overlaid with theoretical CMB signals.

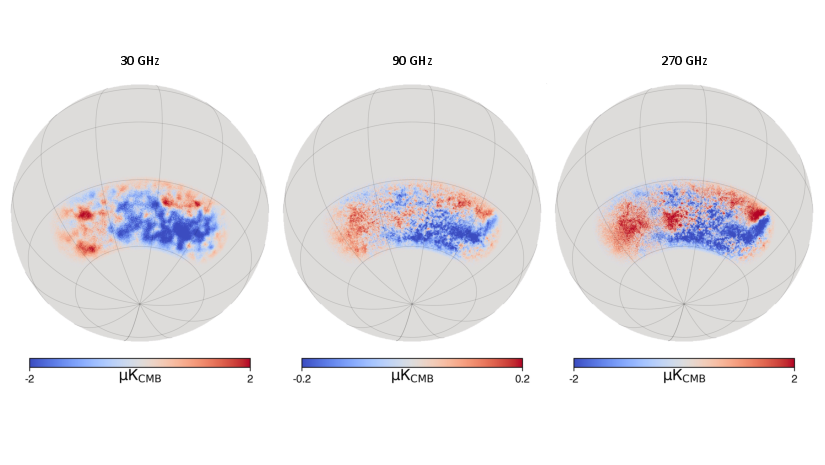
Figure 2: Maps of total simulated $B$-mode observations in three frequency channels, illustrating synchrotron dominance at low frequency (left), dust at high frequency (right), and a CMB channel (middle).

SMICA Pipeline: Model and Implementation

SMICA models the observed multi-frequency $B$-mode data as a linear mixture of independent components (CMB and foregrounds) plus noise. The data covariance in each multipole bin is expressed as:

$$\bm{\mathsf{C}_q} = \bm{\mathsf{A}} \bm{\mathsf{S}_q} \bm{\mathsf{A}}^\dagger + \bm{\mathsf{N}_q}$$

where $\bm{\mathsf{A}}$ is the mixing matrix (encoding frequency scaling), $\bm{\mathsf{S}_q}$ is the component covariance, and $\bm{\mathsf{N}_q}$ is the noise covariance. The CMB mixing vector is fixed (all ones in CMB temperature units), while foreground mixing vectors are unconstrained and normalized at pivot frequencies.

The likelihood is constructed from the Kullback-Leibler divergence between the empirical and model covariances, and is sampled using a No-U-Turn Sampler (NUTS) implemented in JAX/BlackJax for efficient, gradient-based MCMC. Initialization leverages SVD of the noise-whitened data covariance to inform the number of required foreground components ($n_\text{FG}$).

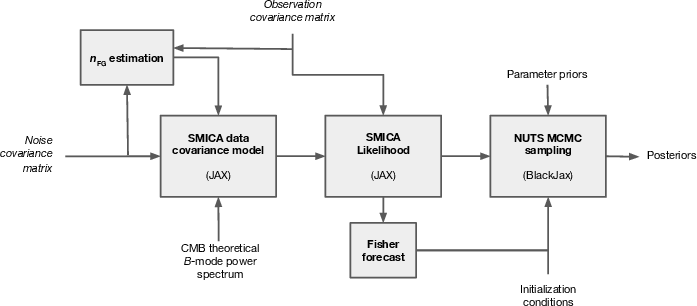
Figure 3: Flowchart describing the SMICA pipeline, from map preprocessing to covariance computation and likelihood sampling.

Results: Bias-Variance Tradeoff and Foreground Modeling

Low-Complexity Foregrounds

For low-complexity foregrounds, a two-component SMICA model ($n_\text{FG}=2$) yields unbiased $r$ estimates with uncertainties matching Fisher forecasts and $\chi^2/n_\text{dof}$ near unity. Overfitting (using $n_\text{FG}>2$) leads to non-convergence, indicating the model's parsimony.

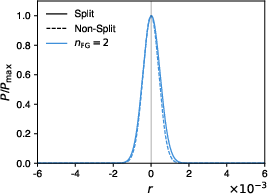
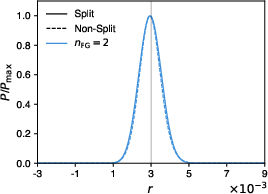
Figure 4: SMICA posterior of $r$ for low-complexity foregrounds, showing unbiased recovery for both $r=0$ and $r=3\times10^{-3}$.

Medium- and High-Complexity Foregrounds

For medium- and high-complexity foregrounds, a two-component model produces significant bias in $r$, with the bias magnitude increasing with foreground complexity. Introducing additional independent components ($n_\text{FG}=3$ or $4$) is necessary to absorb residual foreground power and eliminate bias, at the cost of increased uncertainty in $r$ (demonstrating the bias-variance tradeoff).

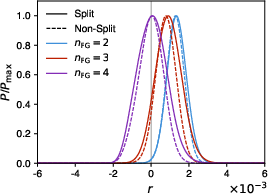
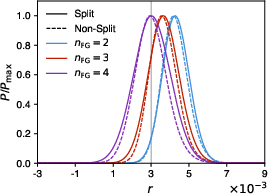
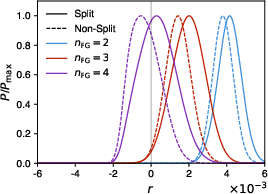
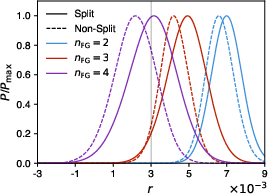
Figure 5: SMICA posterior of $r$ for medium-complexity foregrounds, showing bias with $n_\text{FG}=2$ and unbiased recovery with $n_\text{FG}=4$.

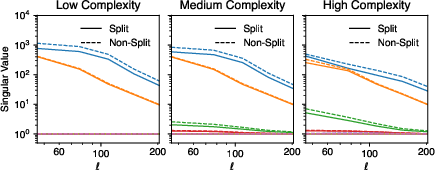
Figure 6: Noise-whitened SVD singular values for low-, medium-, and high-complexity foregrounds, indicating the number of significant independent components required for unbiased modeling.

Foreground Residuals and Model Diagnostics

The SVD of the noise-whitened data covariance robustly determines the number of independent foreground components above the noise floor. For high-complexity foregrounds, four components are required to capture the relevant structure. The $\chi^2/n_\text{dof}$ metric is not sensitive to $r$-bias, as the primordial $B$-mode signal is subdominant in the total covariance. Foreground residuals in the CMB channels are consistent with zero within $1\sigma$ when the appropriate number of components is used.

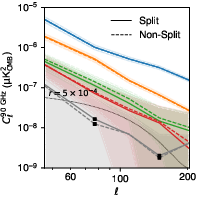
Figure 7: Plots of components in $$\bm{\mathsf{A}} \bm{\mathsf{S}_q} \bm{\mathsf{A}}^\dagger$$ as a function of $\ell$ and frequency, illustrating the complexity and non-power-law behavior of the fitted foregrounds.

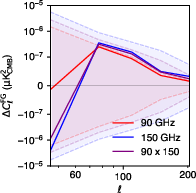
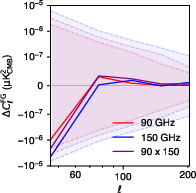
Figure 8: Foreground residuals from the high-complexity, non-split, SMICA best fit, showing reduction in residuals when increasing $n_\text{FG}$ from 2 to 4.

Implications and Future Directions

The results demonstrate that SMICA, when equipped with a sufficient number of independent components, can deliver unbiased $r$ estimates without explicit assumptions about foreground spectral properties. The tradeoff is an increase in statistical uncertainty due to the enlarged parameter space. This approach is robust to unknown or unmodeled foreground complexity, a critical advantage given the limited knowledge of Galactic foregrounds at the required sensitivity.

Hybrid parameterizations—where functional forms are imposed on some components and others are left free—may offer a path to balance flexibility and statistical efficiency. The SVD-based diagnostic is essential for determining model complexity in real data applications.

The findings have direct implications for the design and analysis strategies of current and future CMB experiments targeting PGW detection. In particular, maximizing CMB sensitivity in key frequency bands is more effective than simply increasing the number of frequency channels with higher noise.

Conclusion

This paper establishes that unbiased inference of the primordial tensor-to-scalar ratio $r$ from CMB $B$-mode polarization is achievable with SMICA, provided the model includes a sufficient number of independent foreground components to capture the complexity of Galactic emission. The approach is fully blind with respect to foreground properties, relying on data-driven diagnostics to set model complexity. The bias-variance tradeoff is explicit: reducing bias by increasing model flexibility necessarily increases uncertainty. The methodology and results are directly applicable to the analysis pipelines of current and next-generation CMB experiments seeking to probe inflationary physics via PGWs.