- The paper develops a duality-based minimax framework that enables robust decision making when forecasts are only partially calibrated.
- It reveals a sharp transition where, under decision calibration, the robust policy simplifies to a plug-in best response.
- Empirical evaluations on benchmark datasets show that the robust policy outperforms plug-in methods under adversarial shifts with minimal cost under i.i.d. conditions.
Robust Decision Making with Partially Calibrated Forecasts
Introduction and Motivation
This work addresses the challenge of robust decision making when machine learning forecasts are only partially calibrated. While full calibration ensures that the best policy is to trust the predictions directly, achieving full calibration is computationally intractable in high-dimensional or multiclass settings. The paper introduces a minimax framework for decision making under weaker, more tractable calibration guarantees, characterizing optimal policies and revealing a sharp transition: under decision calibration (a strictly weaker condition than full calibration), the optimal robust policy is again to best respond to the forecast. The analysis extends to generic partial calibration conditions, providing efficient algorithms and empirical validation.
Calibration, Partial Calibration, and Decision Making
Calibration is a statistical property ensuring that, for any predicted value v, the conditional expectation of the outcome given the prediction equals v. Formally, for a forecaster f, full calibration requires E[Y∣f(X)=v]=v for all v. This property guarantees that the best policy for a downstream decision maker is to act as if the forecast is correct.
However, full calibration is infeasible in high dimensions due to exponential sample complexity and computational barriers. As a result, weaker forms of calibration—such as H-calibration—are considered. Here, calibration is enforced only with respect to a set of test functions h∈H, requiring E[h(f(X))⋅(Y−f(X))]=0 for all h∈H. This generalizes to a spectrum of calibration guarantees, with full calibration as the limiting case when H is the set of all measurable functions.
The decision maker, upon receiving a forecast f(x), considers the set of all possible conditional expectations q consistent with the calibration constraints. The robust policy is then defined as the one maximizing expected utility in the worst case over all such q.

Figure 1: Schematic of the interpolating property—robust policies interpolate between minimax safety and best-response as calibration strengthens.
Minimax-Optimal Policies under H-Calibration
The core technical contribution is a duality-based characterization of the minimax-optimal policy under arbitrary finite-dimensional H-calibration. The ambiguity set Q of admissible conditional expectations is defined by the calibration constraints. The robust policy is obtained by solving a saddle-point problem:
arobust(⋅)=arga(⋅)maxq∈QminE[u(a(f(X)),q(f(X)))]
where u(a,y) is the utility function, assumed linear in y. The solution involves:
- Computing dual multipliers λ∗ for the calibration constraints.
- For each forecast v, finding the worst-case q∗(v) by minimizing a convex function involving the dual variables.
- Best-responding to q∗(v).
This approach is computationally efficient for finite H and reduces the robust policy computation to low-dimensional convex programs.
Sharp Transition: Decision Calibration and Best-Response Optimality
A central result is the identification of a sharp transition in the structure of robust policies. When H includes the decision calibration class—indicator functions for the regions where each action is optimal—the robust policy collapses to the plug-in best response:
arobust(v)=arga∈Amaxu(a,v)
This holds for any H containing the decision calibration tests, and the result extends to simultaneous calibration for multiple downstream decision problems. Thus, decision calibration is a minimal, task-specific threshold for robust trustworthiness.
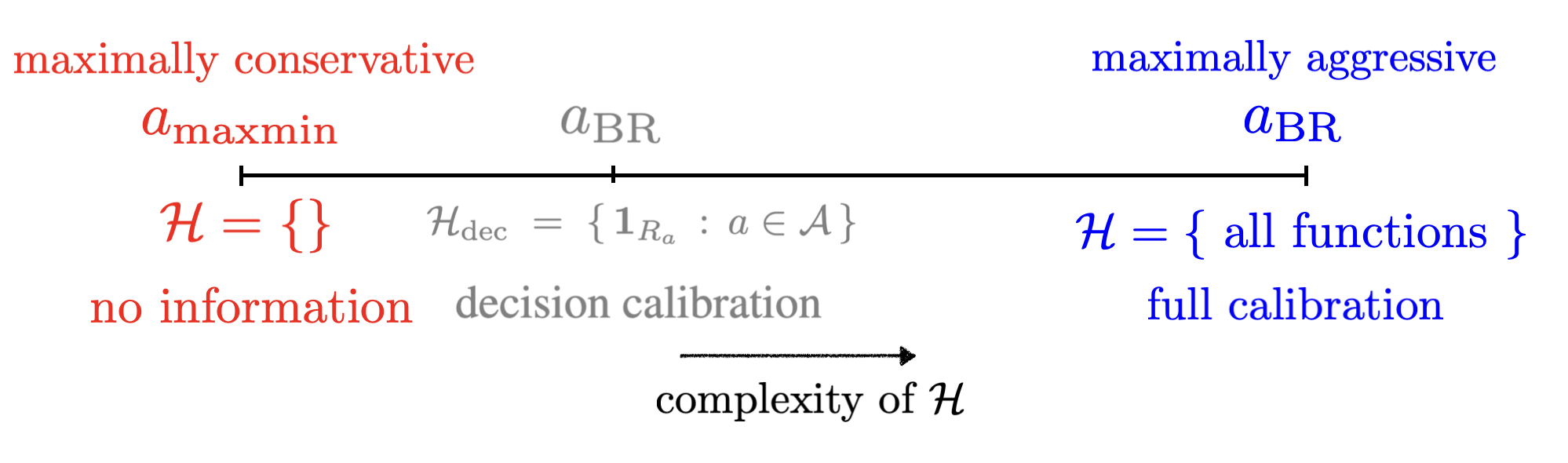
Figure 2: Schematic of the sharp transition—once decision calibration is included, the robust policy collapses to best-response.
Beyond Decision Calibration: Generic Partial Calibration
The framework accommodates generic partial calibration conditions arising from standard training pipelines:
- Self-orthogonality from squared-loss regression: For models with a linear last layer trained by squared loss, the first-order optimality conditions induce calibration with respect to linear test functions. The robust policy is efficiently computable via a penalized dual, and the inner minimization is tractable for finite action sets and linear utilities.
- Bin-wise calibration: Post-hoc recalibration methods (e.g., histogram binning) enforce calibration within bins. The robust policy is piecewise constant: for each bin, best-respond to the mean forecast in that bin.
These results provide practical recipes for robust decision making even when only generic, non-task-specific calibration is available.
Empirical Evaluation
Experiments on the UCI Bike Sharing and California Housing datasets validate the theoretical predictions. A two-layer MLP regressor is trained with squared loss, ensuring self-orthogonality calibration. The robust policy and the plug-in best response are compared under i.i.d. and adversarially shifted test distributions (respecting the calibration constraints).
Key findings:
- Under adversarial shifts tailored to the plug-in policy, the robust policy secures higher utility.
- The cost of robustness under i.i.d. conditions is mild.
- The robust policy dominates the plug-in policy under its own worst-case distribution, as predicted by the minimax theory.
Theoretical and Practical Implications
The results have several implications:
- Theoretical: The sharp transition at decision calibration clarifies the hierarchy of calibration notions and their decision-theoretic consequences. The minimax framework provides a principled foundation for robust decision making under partial calibration.
- Practical: Decision calibration is a tractable and minimal requirement for robust trustworthiness. When unattainable, generic calibration properties from standard training or post-hoc recalibration can still be leveraged for robust policies. The algorithms are efficient and compatible with standard ML pipelines.
Limitations and Future Directions
The analysis assumes risk-neutral decision makers (linear utility in outcomes) and finite action sets. Extending the framework to non-linear utilities or infinite action spaces is a natural direction, though some non-linearities can be handled via basis expansions. Further, the approach relies on the availability of calibration guarantees, which may be challenging to verify or enforce in some settings.
Conclusion
This work establishes a robust, minimax-optimal framework for decision making with partially calibrated forecasts. It demonstrates that decision calibration is a sufficient and minimal condition for best-response optimality, and provides efficient algorithms for robust policies under generic partial calibration. The results bridge the gap between theoretical calibration guarantees and practical, trustworthy decision making in high-dimensional and multiclass settings.



