Autonomous Legged Mobile Manipulation for Lunar Surface Operations via Constrained Reinforcement Learning (2510.12684v1)

Abstract: Robotics plays a pivotal role in planetary science and exploration, where autonomous and reliable systems are crucial due to the risks and challenges inherent to space environments. The establishment of permanent lunar bases demands robotic platforms capable of navigating and manipulating in the harsh lunar terrain. While wheeled rovers have been the mainstay for planetary exploration, their limitations in unstructured and steep terrains motivate the adoption of legged robots, which offer superior mobility and adaptability. This paper introduces a constrained reinforcement learning framework designed for autonomous quadrupedal mobile manipulators operating in lunar environments. The proposed framework integrates whole-body locomotion and manipulation capabilities while explicitly addressing critical safety constraints, including collision avoidance, dynamic stability, and power efficiency, in order to ensure robust performance under lunar-specific conditions, such as reduced gravity and irregular terrain. Experimental results demonstrate the framework's effectiveness in achieving precise 6D task-space end-effector pose tracking, achieving an average positional accuracy of 4 cm and orientation accuracy of 8.1 degrees. The system consistently respects both soft and hard constraints, exhibiting adaptive behaviors optimized for lunar gravity conditions. This work effectively bridges adaptive learning with essential mission-critical safety requirements, paving the way for advanced autonomous robotic explorers for future lunar missions.

• The paper introduces a novel CRL framework that jointly optimizes quadruped locomotion and manipulator control for precise lunar operations.
• The methodology employs a constrained Markov decision process and the ‘Constraints as Terminations’ paradigm, achieving average errors of 4 cm in position and 8.1° in orientation.
• Experimental evaluations using simulation and robotic platforms demonstrate energy-efficient gaits and robust safety compliance under reduced lunar gravity.

Constrained Reinforcement Learning for Autonomous Legged Mobile Manipulation in Lunar Environments

Introduction and Motivation

The paper presents a constrained reinforcement learning (CRL) framework for autonomous control of quadrupedal mobile manipulators in lunar surface operations. The motivation stems from the limitations of wheeled rovers in traversing steep, irregular, and soft regolith-dominated lunar terrains, which necessitate the adoption of legged robots for enhanced mobility and adaptability. The integration of manipulation capabilities with legged locomotion is critical for future lunar missions involving tasks such as sample collection, habitat construction, and equipment maintenance. The proposed approach explicitly addresses the safety-critical requirements of lunar robotics, including collision avoidance, dynamic stability, and power efficiency, under the unique constraints of reduced gravity and unpredictable terrain.

Figure 1: Legged Mobile Manipulator in Lunar environment used in our work.

Methodological Framework

The core contribution is a CRL-based whole-body control architecture that jointly optimizes locomotion and manipulation. The framework is formulated as a constrained Markov Decision Process (CMDP), where the policy must maximize cumulative reward while satisfying a set of hard and soft constraints. The Constraints as Terminations (CaT) paradigm is employed to simplify constraint enforcement, allowing integration with standard RL algorithms such as PPO by probabilistically terminating episodes upon constraint violations.

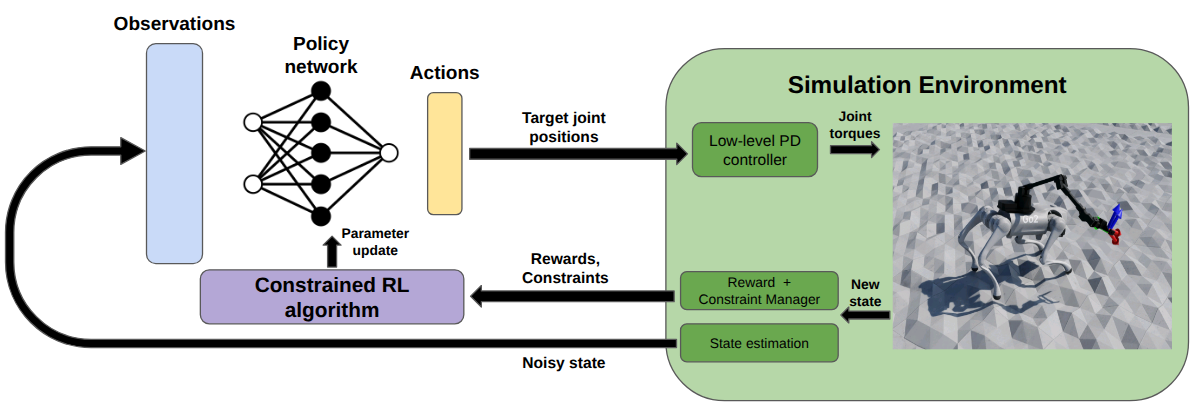
Figure 2: Overview of the proposed methodology.

Task Formulation

• Command Space: The agent receives a 6D end-effector pose command in task space, sampled within a local vicinity to focus on precise manipulation rather than long-range navigation.
• Action Space: The policy outputs desired joint positions for both the manipulator (6 DoF) and quadruped legs (12 DoF), totaling 18 dimensions.
• Observation Space: Includes body orientation, velocities, joint states, previous actions, foot contact states, local terrain height map (via LIDAR), and the desired EE pose (transformed to body frame for learning efficiency).

Reward Design

The reward function is carefully constructed to balance the dual objectives of locomotion and manipulation:

• Pose Tracking Reward: Combines position and orientation errors using an exponential kernel, with the final reward as their product to enforce simultaneous improvement.
• Base Position Reward: Encourages the robot to position its base within a reachable radius of the target EE pose, using a gated exponential function.
• Power Minimization Reward: Rewards low mechanical power consumption for both legs and arm, using an exponential decay on the sum of squared joint powers.

Constraint Specification

• Hard Constraints: Immediate episode termination upon violation, covering non-foot contact forces, excessive body orientation (roll/pitch > 90°), minimum/maximum body height, and maximum foot impact force.
• Soft Constraints: Probabilistic termination, covering joint limits, velocities, torques, body velocity, base rotation, and force distribution across feet (to prevent instability in regolith).

Experimental Evaluation

The framework is implemented using NVIDIA Isaac Sim and Isaac Lab, with a customized constrained PPO algorithm. Training is performed on a Unitree Go2 quadruped with an Interbotix WX250s manipulator, simulating lunar gravity (1/6th Earth) and rough terrain. Domain randomization is applied to mass, control delays, and observation noise for robustness.

• Training Regime: 10,000 iterations, 4096 parallel environments, 10s episodes, policy at 100Hz, PD controllers at 200Hz, single RTX3090 GPU (~5h total training time).
• Constraint Probabilities: Soft constraints use a curriculum from 5% to 90% termination probability; hard constraints are always enforced.

Results

• Pose Tracking Performance: The system achieves an average positional error of 4 cm and orientation error of 8.1°, matching terrestrial state-of-the-art benchmarks. The error distribution is tightly concentrated, with most samples within 2–6 cm position error and <10 cm maximum error.

Figure 3: Distribution of the position and orientation errors for the 4096 evaluated samples.

• Whole-Body Coordination: The robot demonstrates precise and safe EE pose tracking across diverse configurations, leveraging all DoF for complex tasks such as sample collection and surface inspection. Emergent behaviors include energy-efficient gaits and adaptive stabilization exploiting low-gravity conditions.

  Figure 4: Whole-Body EE Pose Tracking Examples. Our legged mobile manipulator shows precise and safe EE pose tracking in difference configurations, allowing its use for tasks such as sample collection or surface inspection.

• Constraint Satisfaction: All hard constraints are strictly respected; soft constraints are violated for less than 0.08% of episode time in the worst case, with an average violation rate of ~0.01%. This demonstrates robust safety compliance under lunar operational conditions.

Implications and Future Directions

The presented CRL framework effectively bridges adaptive learning-based control with formal safety guarantees, a critical requirement for autonomous lunar robotics. The demonstrated performance in simulation suggests strong potential for deployment in real lunar missions, where reliability and self-preservation are paramount due to the irrecoverable nature of failures and communication delays.

Practically, the approach enables legged mobile manipulators to perform complex scientific and operational tasks in extraterrestrial environments, with emergent behaviors that optimize energy consumption and stability under low-gravity. Theoretically, the integration of CaT with whole-body control architectures provides a scalable template for future research in safe RL for high-dimensional robotic systems.

Future work should focus on:

• Extending evaluation to more challenging terrains (e.g., craters, steep slopes).
• Real-world validation in lunar-analog environments.
• Integration with high-level task planning and multi-agent coordination.
• Exploration of more expressive policy architectures and constraint formulations for further robustness.

Conclusion

This paper establishes a constrained reinforcement learning paradigm for autonomous legged mobile manipulation in lunar environments, achieving high-precision 6D pose tracking and robust constraint satisfaction. The results validate the feasibility of CRL for mission-critical space robotics, with implications for both practical deployment and future research in safe, adaptive control of complex robotic systems.